みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
この記事では、平成30年度 電験2種 2次試験 機械・制御 問2の過去問解説をします。
この問題は、同期機に関する基本的な問題です。
同期機のベクトル図が理解できていれば、テンプレート的な回答ができるので、確実に得点源にできるようにしておいてください。
同期機のベクトル図が不安な方は、同期機のベクトル図から出力式を導出する記事も参考にしてください。
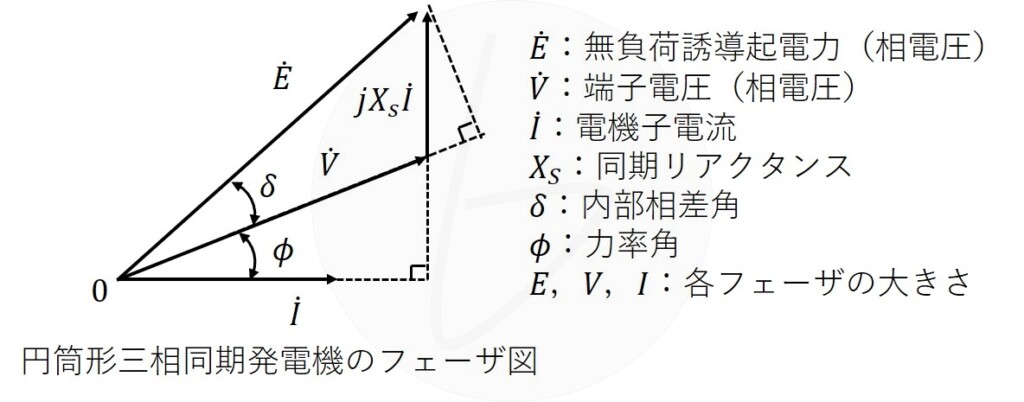
平成30年度 電験2種 2次試験 機械・制御 問2 問題文
図は、三相星形接続の円筒形同期発電機のフェーザ図である。この図を参照して次の問に答えよ。ただし、電機子抵抗による電圧降下及び磁気飽和は無視するものとする。
(1)$E\left[{\rm V}\right]$、$V\left[{\rm V}\right]$、$\delta \left[{\rm rad}\right]$、$X_S\left[{\rm Ω}\right]$を用いて、発電機出力$P\left[{\rm kW}\right]$を表す式を導出過程を含めて示せ。
(2)定格皮相電力$30 000{\rm kV・A}$、定格端子電圧(線間電圧)$6 600{\rm V}$、短絡比$0.5$の円筒形三相同期発電機において、次のa、b及びcの問に答えよ。
a. $X_S\left[\rm{Ω}\right]$の値を求めよ。
b. 三相平衡交流系統に接続して、$E=7 000{\rm V}$、$V=3 810{\rm V}$、$\delta=\frac{\pi}{6}{\rm rad}$で運転しているときの$P\left[{\rm kW}\right]$、$I\left[{\rm A}\right]$、力率($cos\phi$)の値を求めよ。
c . この発電機を三相平衡交流系統から切り離して、三相平衡抵抗器負荷に接続した。界磁電流を調整して$V=3 700{\rm V}$ 、$\delta=\frac{\pi}{3}{\rm rad}$で運転し、抵抗器負荷に電力を供給した。このときの$P\left[{\rm kW}\right]$、$E\left[{\rm V}\right]$、$I\left[{\rm A}\right]$、力率($cos\phi$)の値を求めよ。
解答・解説
同期機に関する典型的な問題です。
設問にあるベクトル図の意味が難しく感じる場合は、同期電動機の等価回路を思い出してみてください。
同期電動機の等価回路は、交流電源と抵抗、インダクタの直列で示される単純なもので、それをベクトル図で表すと、設問のようになります。
小問(1)同期発電機の出力式の導出
ベクトル図の各成分について解図1に示す。

解図1
解図1より、$\dot{V}$ベクトルを基準として、
$$V+X_sIsinϕ=EcosδX_sIcosϕ=Esin\delta \tag{1}$$
となる。
出力は、
$$P=3VIcos\phi×10^{-3}\left[{\rm kW}\right]\tag{2}$$
で示されるので、式(1)から、$Icos\phi$について解くと、
$$Icos\phi=EX_ssin\delta \tag{3}$$
よって、
$$\begin{align}
P&=3VIcos\phi×10-3\\
&=3EVX_ssin\delta×10^{-3}\left[{\rm kW}\right]\tag{4}
\end{align}$$
となる。
(答)$P=3\frac{EV}{X_s}sin\delta\times{10}^{-3}\left[{\rm kW}\right]$
小問(2)
(a)同期リアクタンスの計算問題
短絡比$0.5$より、パーセントリアクタンス$x_s\left[{\rm p.u}\right]$は、
$$x_s=\frac{1}{0.5}=2\left[{\rm p.u.}\right]\tag{5}$$
となる。
さて、定格皮相電力$30 000{\rm kV・A}$、定格端子電圧(線間電圧)$6 600{\rm V}$の条件から、基準インピーダンスを求める。
まず、定格電流$I_n$は、
$$30000×10^3=3×\frac{6600}{\sqrt{3}}×I_n\tag{6}$$
を解いて、
$$In=2624.24242423\left[{\rm A}\right]\tag{7}$$
となる。
基準インピーダンス$Z_{BASE}$は、
$$\begin{align}
Z_{BASE}&=\frac{V_n}{I_n}\\
&=\frac{\frac{6600}{\sqrt{3}}}{2624.24242423}\\
&=1.452085189\tag{8}
\end{align}$$
である。以上より、
$$\begin{align}
X_s&=x_sZ_{BASE}\\
&=2×1.452085189\\
&=2.904170378\tag{9}
\end{align}$$
となる。
(答)$X_s=2.90\left[{\rm Ω}\right]$
(b)同期発電機の各物理量の計算問題(三相平衡系統連系時)
小問(1)の結果より、
$$\begin{align}
P&=3\frac{EV}{X_s}sinδ×10^{-3}\\
&=3\frac{7000×3810}{2.904170378}sin\frac{π}{6}×10^{-3}=13775.0182644\left[{\rm kW}\right]\tag{10}
\end{align}$$
式(1)より、
$$Isin\phi=\frac{Ecosδ-V}{X_s}\tag{11}$$
$$Icos\phi=\frac{E}{X_s}sinδ\tag{12}$$
である。
$I^2\left(sin^2\phi+cos^2\phi\right)=I^2$より、
$$\begin{align}
I^2&=\left(\frac{Ecos\delta-V}{X_s}\right)^2+\left(\frac{E}{X_s}sin\delta\right)^2\\
&=\left(\frac{7000\times c o s\frac{\pi}{6}-3810}{2.904170378}\right)^2+\left(\frac{7000}{2.904170378}sin\frac{\pi}{6}\right)^2\\
&=2053720.86634\tag{13}
\end{align}$$
となる。
以上より、
$$I=\sqrt{2053720.86634}=1433.08090013\tag{14}$$
となる。
式(12)より、
$$\begin{align}
cosϕ&=\frac{E}{X_sI}sin\delta\\
&=\frac{7000}{2.904170378×1433.08090013}sin\frac{\pi}{6}\\
&=0.84095981782\tag{15}
\end{align}$$
となる。
(答)$P=1.38×{10}^4\left[{\rm kW}\right]$、$I=1430\left[{\rm A}\right]$、$cos\phi=0.841$
(c)同期発電機の各物理量の計算問題(力率1の時)
題意より、三相抵抗負荷を接続しているので力率は1になる。ベクトル図は解図2になる。

解図2
ベクトル図の実軸成分より、
$$Ecosδ=V$$
であり、$V=3700{\rm V}$ 、$\delta=\frac{\pi}{3}{\rm rad}$であるから、
$$Ecos\frac{π}{3}=3700\tag{16}$$
より、$E=7400\left[{\rm V}\right]$となる。
また、ベクトル図の虚軸成分より、
$$Esinδ=X_sI\tag{17}$$
であるから、
$$7400sin\frac{\pi}{3}=2.904170378I$$
を解いて、$I=2206.61984866\left[{\rm A}\right]$となる。
出力$P\left[{\rm kW}\right]$について、
$$\begin{align}
P&=3VI×10^{-3}\\
&=3×3700×2206.61984866×10^{-3}\\
&=24493.4803201\left[{\rm kW}\right]\tag{18}
\end{align}$$
となる。
(答)$P=2.45×{10}^4\left[{\rm kW}\right]$、$E=7400\left[{\rm V}\right]$、$I=2.21×{10}^3\left[{\rm A}\right]$、$cos\phi=1.00$
関連コンテンツ
この問題の内容は、同期発電機の出力式の記事(ベクトル図からの導出)を参考にしてください。
その他、電験2種2次試験では、無負荷誘導起電力や内部相差角の計算問題も出題されています。
これらの内容は、同期発電機の特性計算の記事を参考にしてください。
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






