【H30 電験2種 2次機械・制御問3】三相サイリスタ変換器の計算問題

みなさん、こんにちは！

ブリュの公式ブログ.org（for Academic Style）にお越しいただきまして、ありがとうございます！

この記事では、平成30年度電験2種 2次試験機械・制御問3の過去問解説をします。

問題となっている三相サイリスタ変換器は回路図の素子が多く、波形も登場しているため一見難易度が高そうですが、順番に解いていけば、基本的には三相全波整流回路の知識で解ける問題です。

途中、小問（5）が難易度が高めですが、この記事ではわかりやすく解説したので、類題が出題された時には確実に得点源にできるようにしておいてください。

小問（5）は回路構造の対称性を利用すれば、直感的に解けます。

平成30年度電験2種 2次試験機械・制御問3 問題文

図1に三相サイリスタ変換器を2台使用した変換装置を示す。対称三相電圧の①系統、②系統に接続されている変換器をそれぞれ変換器1、変換器2とし、その直流電圧を$v_{dc1}$、$v_{dc2}$とする。①系統の相順は$u$→$v$→$w$相とし、変換器1のサイリスタの番号を図1に示す。直流リアクトル$L$のインダクタンスは十分に大きく、直流電流$I_d$のリプルは無視できる。また、図示されていない回路内のインピーダンス及び回路内の損失も無視できるものとする。なお、$I_d$、$v_{dc1}$、$v_{dc2}$の極性は、図1に示す方向を正とする。動作は定常状態にあるものとして、次の問に答えよ。

（1）ある時刻に変換器1のサイリスタ$T_1$及び$T_5$がオンしていたとする。電気角で$120°$に相当する時間後に通電しているのはどのサイリスタであるかを示せ。

（2）①系統の三相交流線間電圧の実効値を$V_1$とする。変換器1を図2に示す制御角$\alpha_1$で運転したときに、直流電圧$v_{dc1}$の平均値$V_{dc1}$を求める式を、$V_1$及び$\alpha_1$を用いて示せ。

（3）損失がないとしているので、この装置における①系統から入力される有効電力$P_{ac1}$と直流電力$P_{dc}$とは等しい。有効電力$P_{ac1}$を表す式を$V_1$、$I_d$及び$\alpha_1$を用いて示せ。

（4）①系統に流れる波高値$I_d$の交流の線電流は半サイクルで$120°$通電の方形波となり、この波形に含まれる基本波実効値$I_1$は$\frac{\sqrt{6}}{\pi}I_d$である。この基本波による①系統からの遅れの無効電力$Q_{ac1}$を表す式を、$V_1$、$I_d$及び$\alpha_1$を用いて示せ。

（5）変換器2の直流電圧$v_{dc2}$の平均値を$V_{dc2}$とする。①系統から②系統に電力を送る場合、電流$I_d$の極性は正、平均電圧$V_{dc1}$、$V_{dc2}$の両方の極性とも正である。逆に、②系統から①系統に電力を送る場合に、電流$I_d$、平均電圧$V_{dc1}$、$V_{dc2}$の極性は正であるか負であるかを示せ。

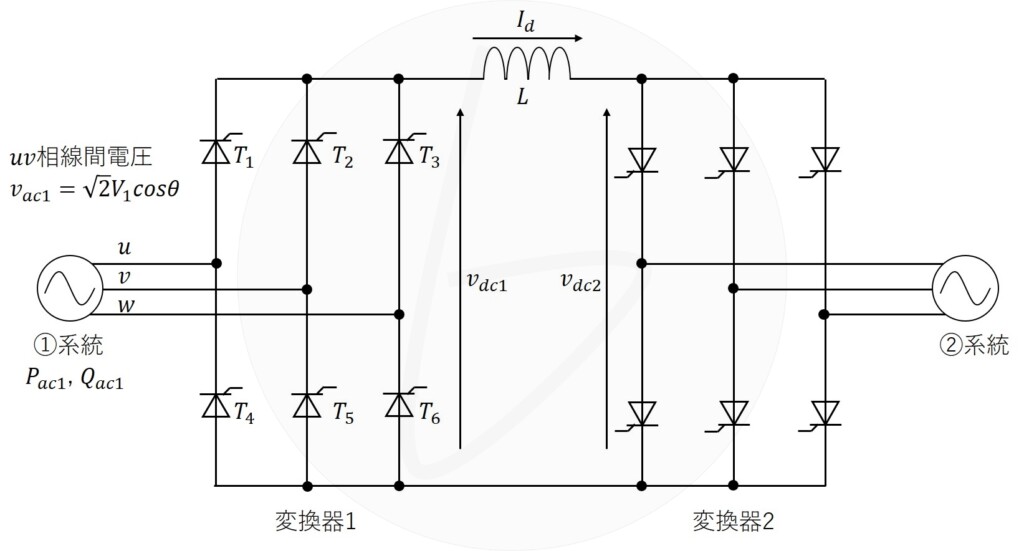
図1　三相サイリスタ整流回路の変換器を2台使用した変換装置

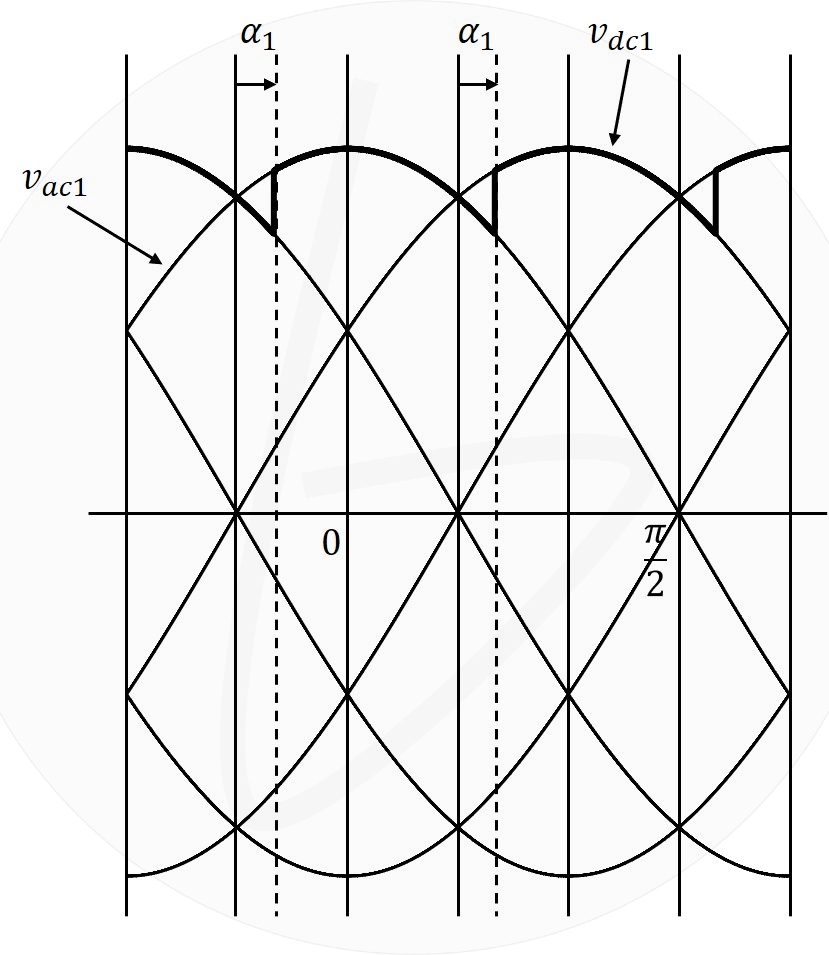
図2　交流線間電圧と直流電圧の関係

解答・解説

小問（1）三相全波整流回路の動作解析

解図1に三相全波整流回路の電圧波形を示す。

サイリスタ$T_1$及び$T_5$がオンしている状況から、$u-v$間の電圧が出力されていると考えることができる。

各線間電圧は、それぞれ$60°$ずつ出力されているので、電気角で$120°$後には、$v-w$間の線間電圧が出力される。

つまり、サイリスタ$T_2$及び$T_6$が通電する。

解図1

（答）サイリスタ$T_2$及び$T_6$が導通する。

小問（2）直流電圧の平均値の計算

解図2より、$-\frac{\pi}{6}+\alpha_1$から$\frac{\pi}{6}+\alpha_1$の間で平均電圧を計算すれば、線間電圧が、

$$\sqrt{2}V_1cos\theta \tag{1}$$

で表せるので、

$$\begin{align}
V_{dc1}&=\frac{1}{\frac{\pi}{3}}\int_{-\frac{\pi}{6}+\alpha_1}^{\frac{\pi}{6}+\alpha_1}{\sqrt{2}V_1cos\theta d\theta}\\
&=\frac{3\sqrt{2}}{\pi}V_1\left[sin\theta\right]_{-\frac{\pi}{6}+\alpha_1}^{\frac{\pi}{6}+\alpha_1}\\
&=\frac{3\sqrt{2}}{\pi}V_1\left\{sin\left(\frac{\pi}{6}+\alpha_1\right)-sin\left(-\frac{\pi}{6}+\alpha_1\right)\right\}\\
&=\frac{3\sqrt{2}}{\pi}V_1\left(\frac{1}{2}cos\alpha_1+\frac{\sqrt3}{2}sin\alpha_1+\frac{1}{2}cos\alpha_1-\frac{\sqrt3}{2}sin\alpha_1\right)\\
&=\frac{3\sqrt2}{\pi}V_1cos\alpha_1\\
&=1.35095541401V_1cos\alpha_1\tag{2}
\end{align}$$

となる。

解図2

（答）$V_{dc1}=1.35V_1cos\alpha_1$

小問（3）有効電力の計算

直流電流$I_d$のリップルが無視でき、一定とみなせるので、

$$\begin{align}
P_{ac1}&=\frac{1}{2\pi}\int_{0}^{2\pi}v_{dc1}I_dd\theta\\
&=I_d・\frac{1}{2π}\int_{0}^{2π}v_{dc1}dθ\\
&=I_d・V_{dc1}\\
&=\frac{3\sqrt{2}}{π}V_1I_dcos\alpha_1\\
&=1.35095541401V_1I_dcos\alpha_1 \tag{3}
\end{align}$$

となる。

（答）$P_{ac1}=1.35V_1I_dcos\alpha_1$

小問（4）無効電力の計算

本問のポイントは、基本波力率$\theta$と制御角$\alpha$の関係として、

$$cos\theta=cos\alpha$$

の関係にあることを知っていることです。

下図に示す通り、波高値$I_d$、半サイクル$120°$通電の方形波電流なので、$u$相には青の点線で示すような電流が流れています。

この方形波電流について、$u$相に流れている基本波成分を取り出せば青線で示す電流波形となります。

さて、

赤線で示す$u$相基本波電圧波形
青線で示す$u$相基本波電流波形

を比較すれば、電流波形は電圧波形に対してちょうど$\alpha$だけ遅れている、まさに力率$cos\alpha$の状態になっているので、制御角$\alpha$がそのまま力率$\theta$になることがわかります。

系統1が供給する基本波の皮相電力は、

$$\begin{align}
S_{ac1}&=3・\frac{V_1}{\sqrt{3}}・I_1\\
&=3\frac{V_1}{\sqrt{3}}・\frac{\sqrt{6}}{π}I_d\\
&=\frac{3\sqrt{2}}{π}V_1I_d \tag{4}
\end{align}$$

である。

また、制御角$\alpha_1$であることから力率$\theta$であることがわかるので、無効電力$Q_{ac1}$は、

$$\begin{align}
Q_{ac1}&=S_{ac1}sin\alpha_1\\
&=\frac{3\sqrt2}{\pi}V_1I_dsin\alpha_1\\
&=1.35095541401V_1I_dsin\alpha_1 \tag{5}
\end{align}$$

となる。
（答）$Q_{ac1}=1.35V_1I_dsin\alpha_1$