みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、制御理論の基礎となる、伝達関数とブロック線図です。
ブロック線図は、信号の流れをブロックで示すものであり、制御システムの直感的な理解に役立ちます。
また、現代制御理論では、古典制御のブロック線図が進化して登場します。
古典制御理論・現代制御理論を理解するには必須になる内容なので確実に理解しておいてください。
▼おすすめ記事▼

伝達関数とブロック線図の重要事項
伝達関数の要点
伝達関数とは、入力信号$x\left(t\right)$、出力信号$y\left(t\right)$とし、そのラプラス変換したものをそれぞれ$X\left(s\right)$、$Y\left(s\right)$とすれば、その比率を$G\left(s\right)$は、
$$G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}$$
で計算できて、これを伝達関数という。
なお、ラプラス変換によって微分積分計算を含めすべて四則演算で計算できる。
すなわち、伝達関数は四則演算のみで表現が可能である。
ブロック線図の要点
伝達関数はブロック線図で示せ、下図のようになる。
ブロック線図は、入力信号$X\left(s\right)$が$G\left(s\right)$倍されることで出力信号$Y\left(s\right)$になることを意味している。
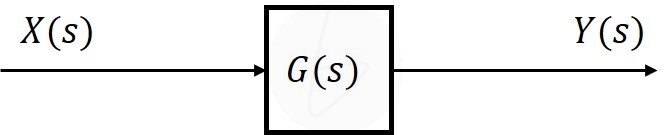
その他、ブロック線図における加算・減算は加え合わせ点、信号分岐は引出し点で表現できる。
これによって、四則演算で示される伝達関数を図示することができる。
.jpg) (a)加え合わせ点(加算の場合) |
.jpg) (b)加え合わせ点(減算の場合) |
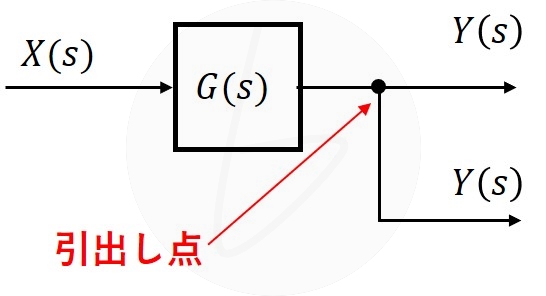 (c)引出し点 |
|
伝達関数とは何なのか
入出力の比率を表す伝達関数
以前、ラプラス変換は微分・積分を含めたあらゆる計算を、
- 掛け算
- 割り算
- 足し算
- 引き算
の四則演算に移す写像であることを説明しました。
つまり、入力信号$x\left(t\right)$と出力信号$y\left(t\right)$をラプラス変換し、それぞれ$X\left(s\right)$、$Y\left(s\right)$とすれば、比率$G\left(s\right)$を計算することができて、
$$G(s)=\frac{Y\left(s\right)}{X\left(s\right)}\tag{1}$$
となります。
この$G\left(s\right)$を伝達関数といいます。
式(1)を変形すれば、伝達関数$G\left(s\right)$とは、ある入力$X\left(s\right)$と出力$Y\left(s\right)$の関係について、
$$Y\left(s\right)=G\left(s\right)X\left(s\right)\tag{2}$$
となり、入力$X\left(s\right)$に伝達関数$G\left(s\right)$をかけることで、出力$Y\left(s\right)$が求まります。
連続した伝達関数
では、伝達関数が連続してる場合を考えてみます。
例えば、
$$\begin{cases}
Y_1\left(s\right)=G_1\left(s\right)X\left(s\right)\\
Y_2(s)=G_2(s)Y_1(s)\\
Y(s)=G_3(s)Y_2(s)
\end{cases}\tag{3}$$
といった関係があった場合、順に代入していけば、
$$Y(s)=G_3(s)Y_2(s)=G_3(s)G_2(s)Y_1(s)=G_3(s)G_2(s)G_1(s)X(s)\tag{4}$$
となります。
つまり、
$$\frac{Y(s)}{X(s)}=G_1(s)G_2(s)G_3(s)\tag{5}$$
となります。
以上より、伝達関数が連続していれば、それらすべての積が、システムの合成された伝達関数になります。
制御理論は、こうした伝達関数について、制御信号の流れが、
直列:掛け算や割り算
並列:足し算や引き算
で示し、代数演算を行うものです。
抽象的な話でなかなか理解が難しいと思うので、次節のブロック線図の項目へと読み進めてください。
ブロック線図による制御系の表現
伝達関数は、様々な基本関数や微分・積分で示される入出力関係を、ラプラス変換によって四則演算に変換し、比率として示したものです。
そして、この伝達関数は「ブロック線図」として図示できます。この節では、ブロック線図によって示される$s$領域の四則演算、および等価変換による簡単化について説明していきます。
掛け算・割り算を表現する「ブロック」
ブロック線図は、入力~出力の経路において、どのような伝達関数が作用するかを図示したものです。
もっとも簡単な伝達関数である、
$$G(s)=\frac{Y(s)}{X(s)}\tag{6}$$
に対応するブロック線図を、図1に示します。
ブロック線図のブロックは掛け算や割り算を示しており、ブロックに入った信号波、$G(s)$倍されて出力されます。
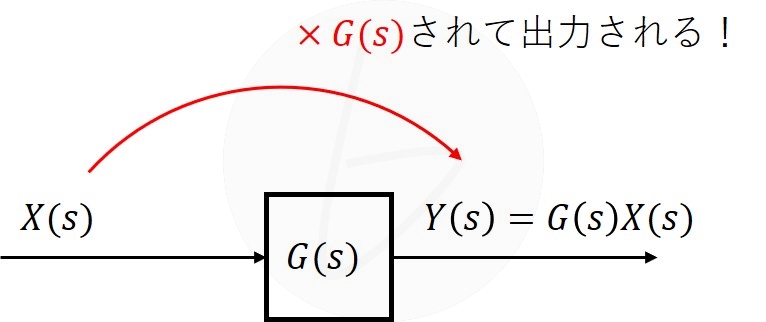
図1 ブロック線図の基本
これにより、先ほど式(3)、式(4)で示した伝達関数は、ブロック線図において図3のように示されます。
$$\begin{cases}
Y_1\left(s\right)=G_1\left(s\right)X\left(s\right)\\
Y_2(s)=G_2(s)Y_1(s)\\
Y(s)=G_3(s)Y_2(s)
\end{cases}\tag{再掲3}$$
$$Y(s)=G_3(s)Y_2(s)=G_3(s)G_2(s)Y_1(s)=G_3(s)G_2(s)G_1(s)X(s)\tag{再掲4}$$
は下図のような理解ができます。
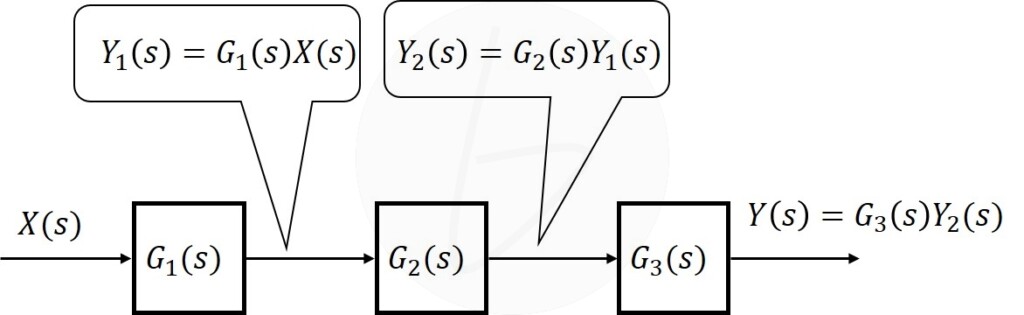
図2 連続したブロック線図(伝達関数の掛け算・割り算表現)
(a)3つのブロックで表現 (b)1つのブロックにまとめる
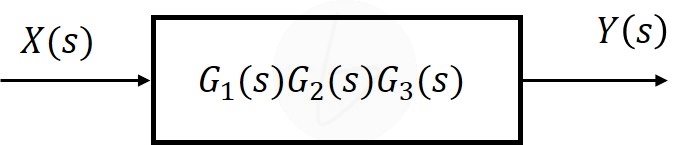
図3 ブロック線図の簡単化
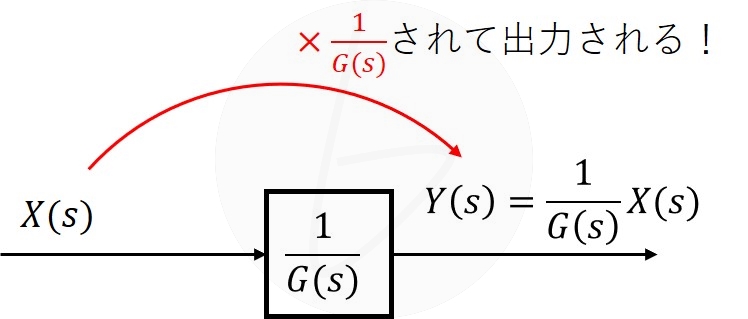
参考に、ブロックの要素を$\frac{1}{G\left(s\right)}$にすれば、割り算を表現できます。
足し算・引き算を表現する「加え合わせ点」と「引出し点」
ブロック線図には、図2.2.4に示すような「加え合わせ点」があり、足し算、引き算も表現できます。
.jpg) (a)加算の場合 |
.jpg) (b)減算の場合 |
図2.2.4 伝達関数の加え合わせ点
引出し点では、信号が分岐します。信号が分岐して、並列に流れ、最終的に加え合わせ点で合流するような表現が多用されます。

図2.2.5 伝達関数の引出し点
ブロック線図の例
例えば、
Gs=YsXs=G1sG2s+G3s#2.2.1
というような伝達関数をブロック線図で示す場合、図2.2.6のようになります。
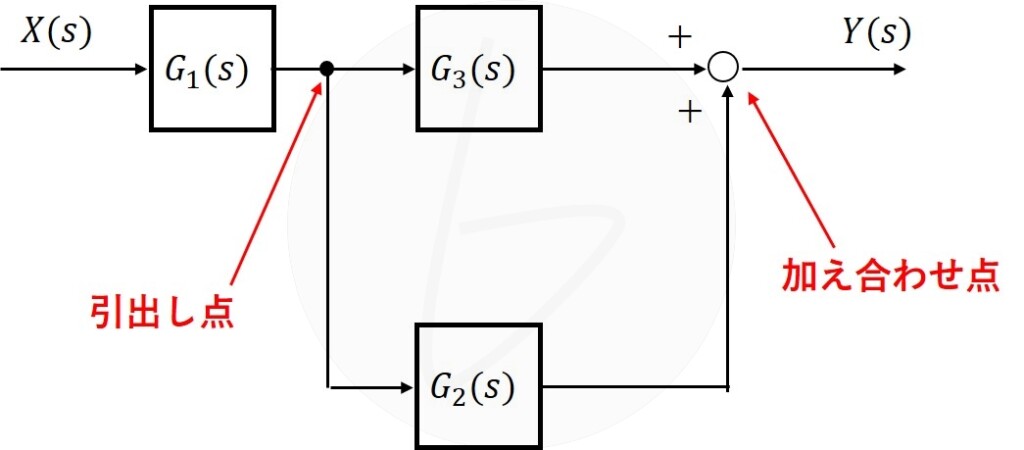
図2.2.6 伝達関数の例
以上、ブロック線図では、ブロックそのものが掛け算、割り算を示し、加え合わせ点、引出し点が足し算、引き算を表現します。
これでブロック線図では四則演算がすべて表現できるので、あらゆる伝達関数はブロック線図で表現できることがわかりました。
まとめ
ここまで、伝達関数とブロック線図について説明してきました。
ブロック線図は、等価変換の話が出てきます。
ブロック線図の等価変換を見れば、よりイメージがつかみやすくなるでしょう。
また、制御の本質は、出力を目標値と一致されることにあり、これはまさにフィードバック制御になります。
フィードバック制御の身近な例とともに、フィードバック制御系の伝達関数・ブロック線図のことも紹介しているので、以下の記事も参考にしてみてください。
→フィードバック制御の身近な例と伝達関数・ブロック線図について
ラプラス変換による具体的な解法も含めて、わかりやすいように説明しました。
●紙の本:3,850円(税込)
電験2種 二次試験 機械・制御で出題される自動制御を完答することを目的に作成した参考書。
機械・制御において、自動制御で満点を狙い、確実に合格したい場合には、この参考書がおすすめです。




