みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、同期発電機のベクトル図から、
- 同期発電機の無負荷誘導起電力
- 同期発電機の内部相差角(負荷角)
について導出を行います。
▼おすすめ記事▼
同期発電機の無負荷誘導起電力と内部相差角(負荷角)の公式
無負荷誘導起電力$E_0$と内部相差角(負荷角)$\delta$は同時に導出できるので関連付けて理解しておきましょう。
無負荷誘導起電力の公式
同期発電機の無負荷誘導起電力は、
$$E_0=\sqrt{V^2+{Z_0}^2I^2+2VI(r_acos\theta+x_ssin\theta)} \tag{1}$$
となります。
ただし、
- $V$:端子電圧
- $I$:電流
- $Z_0=\sqrt{r_a^2+x^2}$:同期インピーダンス
- $r_a$:電機子抵抗
- $x_s$:同期リアクタンス
となります。
無負荷誘導起電力は、同期発電機の巻線部分に発生している起電力のことであり、無負荷端子電圧と同じです。
内部相差角(負荷角)の公式
同期発電機の内部相差角(負荷角)は、
$$\delta=tan^{-1} \left(\frac{x_sIcos\theta-r_aIsin\theta}{V+r_aIcos\theta+x_sIsin\theta}\right) \tag{2}$$
となります。
ただし、
- $V$:端子電圧
- $I$:負荷電流
- $r_a$:電機子抵抗
- $x_s$:同期リアクタンス
- $\theta$:力率角
となります。
内部相差角(負荷角)は、無負荷誘導起電力$\dot{E_0}$と端子電圧$\dot{V}$の位相差のことです。
一般的な位相の相対関係として、
端子電圧$\dot{V}$は無負荷誘導起電力$\dot{E_0}$に対して遅れ位相
逆に言えば、
無負荷誘導起電力(負荷角)\dot{E_0}は端子電圧$\dot{V}$に対して進み位相
になります。
また、$\delta=\frac{\pi}{2}$[rad]のとき、電気出力が最大になることも押さえておきましょう。
同期発電機の無負荷誘導起電力の導出
では、同期発電機の無負荷誘導起電力の式を導出します。
同期発電機の回路図とベクトル図
図1に、同期発電機の回路図を示します。
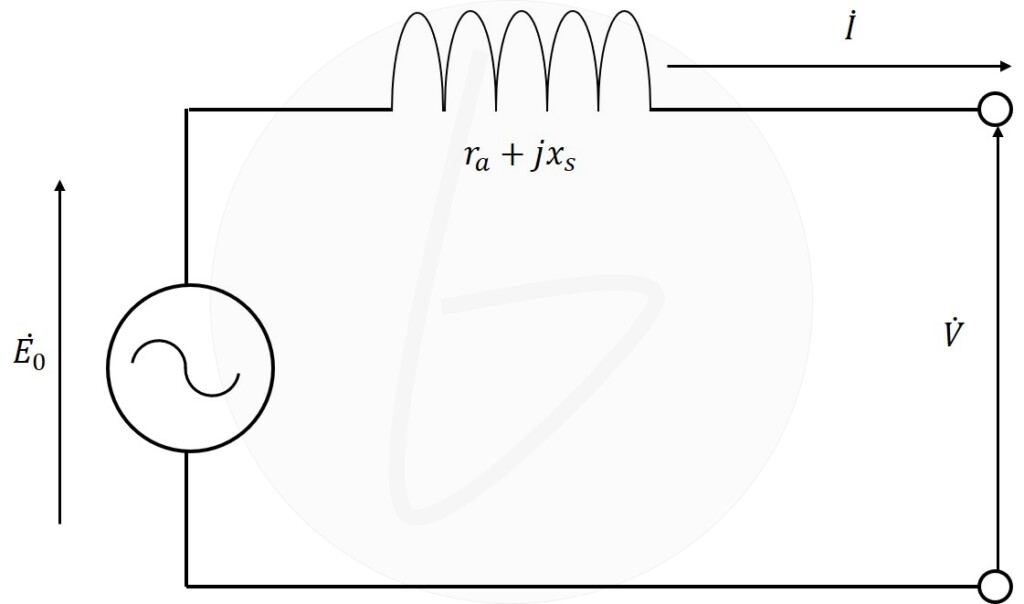
図1 同期発電機の等価回路
同期発電機の等価回路に従って、同期発電機のベクトル図を描くと、図2のようになります。
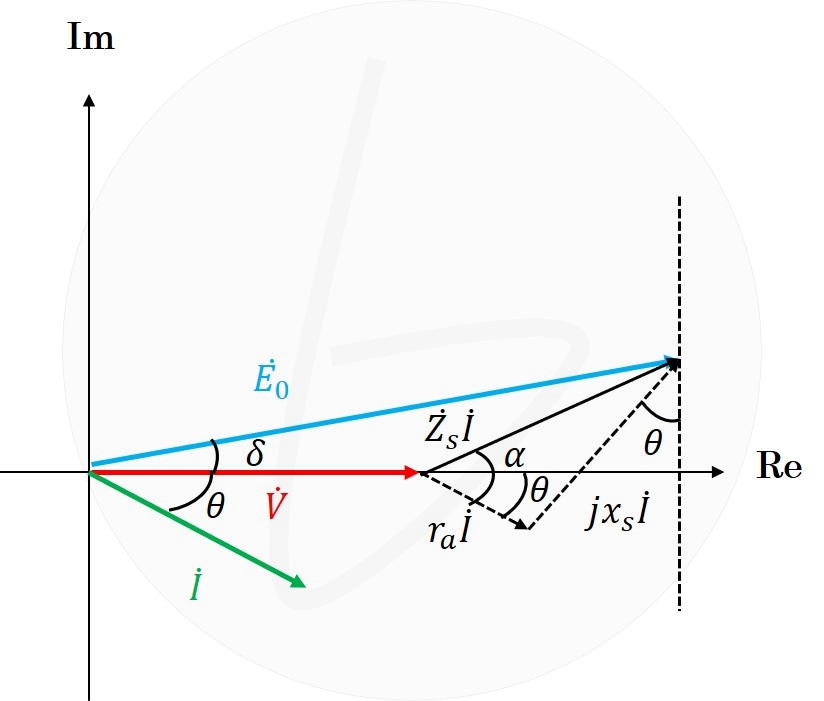
図2 同期発電機のベクトル図
実軸成分の計算
まずは、実軸成分について考えましょう。
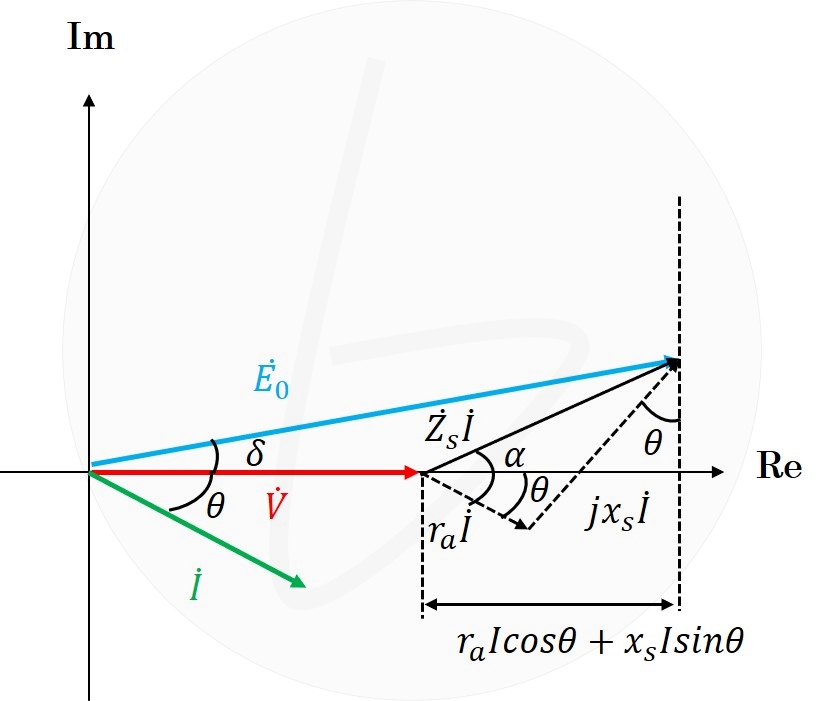
図3 同期発電機のベクトル図(実軸の計算)
図3に示すベクトル図より、実軸成分の式は、
$$V+r_aIcos\theta+x_sIsin\theta=E_0cos\delta \tag{3}$$
となります。
両辺を2乗して、右辺と左辺を入れ替えておきます。
$$(E_0cos\delta)^2=(V+r_aIcos\theta+x_sIsin\theta)^2 \tag{4}$$
虚軸成分の計算
次に、虚軸成分を見ていきます。
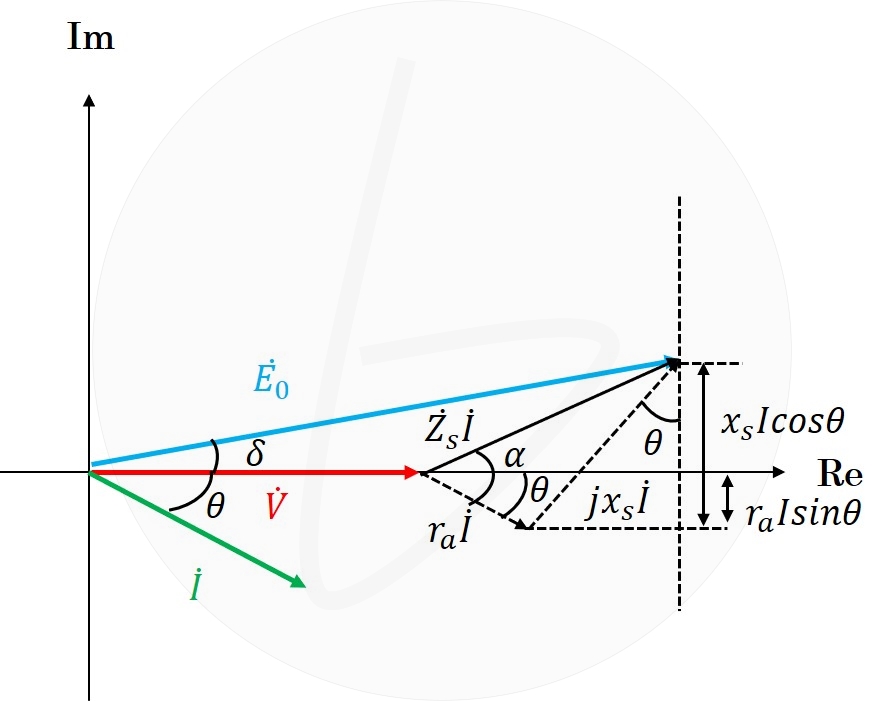
図4 同期発電機のベクトル図(虚軸の計算)
図4に示すベクトル図より、虚軸成分は、
$$x_sIcos\theta-r_aIsin\theta=E_0sin\delta \tag{5}$$
となります。
実軸と同様に、両辺を2乗して、右辺と左辺を入れ替えておきます。
$$(E_0sin\delta)^2=(x_sIcos\theta-r_aIsin\theta)^2 \tag{6}$$
同期発電機の無負荷誘導起電力
これで、式(4)と式(6)から、
実軸:$(E_0cos\delta)^2=(V+r_aIcos\theta+x_sIsin\theta)^2$
虚軸:$(E_0sin\delta)^2=(x_sIcos\theta-r_aIsin\theta)^2$
となりました。
和を計算すると、
$$(E_0cos\delta)^2+(E_0son\delta)^2=(V+r_aIcos\theta+x_sIsin\theta)^2+(x_sIcos\theta-r_aIsin\theta)^2 \tag{7}$$
$cos^2\delta+sin^2\delta=1$より、式(7)の左辺は$E_0^2$になるので、
$$\begin{align}
{E_0}^2 &=(V+r_aIcos\theta+x_sIsin\theta)^2+(x_sIcos\theta-r_aIsin\theta)^2 \\
&=V^2+{r_a}^2I^2cos^2\theta+{x_s}^2I^2sin^2\theta+2Vr_aIcos\theta+2r_ax_sI^2sin\theta cos\theta+2Vx_sIsin\theta\\
&+{x_s}^2I^2cos^2\theta-2r_ax_sI^2sin\theta cos\theta+{r_a}^2I^2sin^2\theta\\
&=V^2+{r_a}^2I^2+{x_s}^2I^2+2Vr_aIcos\theta+2Vx_sIsin\theta \tag{8}
\end{align}$$
${Z_0}^2={r_a}^2+{x_s}^2$より、
$$\begin{align}
{E_0}^2&=V^2+{Z_0}^2I^2+2Vr_aIcos\theta+2Vx_sIsin\theta\\
&=V^2+{Z_0}^2I^2+2VI(r_acos\theta+x_ssin\theta) \tag{9}
\end{align}$$
$$E_0=\sqrt{V^2+{Z_0}^2I^2+2VI(r_acos\theta+x_ssin\theta)} \tag{10}$$
となります。
これが、同期発電機の無負荷誘導起電力になります。
無負荷の際には電機子電流が流れず、同期インピーダンス$\dot{Z_s}$による電圧降下もないです。
そのため、無負荷誘導起電力は、同期発電機を無負荷にしたとき、出力端子に現れる電圧に等しいです。
内部相差角(負荷角)の導出
途中、式(3)及び式(5)までは無負荷誘導起電力$E_0$の導出と同じです。
実軸に関する式(3)より、
$$cos\delta=\frac{V+r_aIcos\theta+x_sIsin\theta}{E_0} \tag{11}$$
であり、虚軸に関する式(5)より、
$$sin\delta=\frac{x_sIcos\theta-r_aIsin\theta}{E_0} \tag{12}$$
となります。
ここで、$tan\delta=\frac{sin\delta}{cos\delta}$より、
$$tan\delta=\frac{\frac{x_sIcos\theta-r_aIsin\theta}{E_0}}{\frac{V+r_aIcos\theta+x_sIsin\theta}{E_0}} \tag{13}$$
すなわち、$E_0$が約分できて、
$$tan\delta=\frac{x_sIcos\theta-r_aIsin\theta}{V+r_aIcos\theta+x_sIsin\theta} \tag{14}$$
となります。
内部相差角(負荷角)$\delta$は、
$$\delta=tan^{-1} \left(\frac{x_sIcos\theta-r_aIsin\theta}{V+r_aIcos\theta+x_sIsin\theta}\right) \tag{15}$$
となります。
まとめ
以上で、
■同期発電機の無負荷誘導起電力
$$E_0=\sqrt{V^2+{Z_0}^2I^2+2VI(r_acos\theta+x_ssin\theta)}$$
■同期発電機の内部相差角(負荷角)
$$\delta=tan^{-1} \left(\frac{x_sIcos\theta-r_aIsin\theta}{V+r_aIcos\theta+x_sIsin\theta}\right)$$
の導出ができました。
同期発電機のベクトル図が分かれば、実軸と虚軸の計算をするだけで求められるので、導出も含めてマスターしておきましょう。