配電系統の電力損失を低減することはエネルギー資源の効率的な活用に有用である。次の問に答えよ。
(1)柱上変圧器を重負荷地点近傍に設置することは、電力損失を低減する方策の一つである。これ以外の配電系統の電力損失低減策を三つ述べよ。
(2)柱上変圧器を重負荷地点近傍に設置することによる電力損失低減効果について、a)平等負荷分布(各地点での負荷電流が同じ)及びb)不平等負荷分布における電力損失を求めることにより、b)がa)より小さくなることを示したい。
a)図1に示すように、平等負荷分布である単相2線式の低圧配電系統において、電線こう長$L\left[{\rm m}\right]$、A点から$x\left[{\rm m}\right]$だけ離れた地点の線路電流$I_x\left[{\rm A}\right]$を求めたうえで、低圧配電線の全区間の電力損失を$I_s$、$L$、$r$を用いて求めよ。ただし、変圧器二次側の送電線電流$I_s\left[{\rm A}\right]$、電線単位長抵抗$r\left[{\rm Ω/m}\right]$とし、配電線路の線路特性は均一として、電源電圧は一定であるものとする。
b)図2に示すように、末端へ行くほど直線的に減少する不平等負荷分布である単相2線式の低圧配電系統において、A’点から$x’\left[{\rm m}\right]$だけ離れた地点の負荷電流密度$i_x’\left[{\rm A/m}\right]$及び線路電流$I_x’\left[{\rm A}\right]$を、A’点の負荷電流密度$i_0’\left[{\rm A/m}\right]$を用いて求めたうえで、低圧配電線の全区間の電力損失を$I_s$、$L$、$r$を用いて求めよ。ただし、電流分布以外の条件はa)と同様とする。
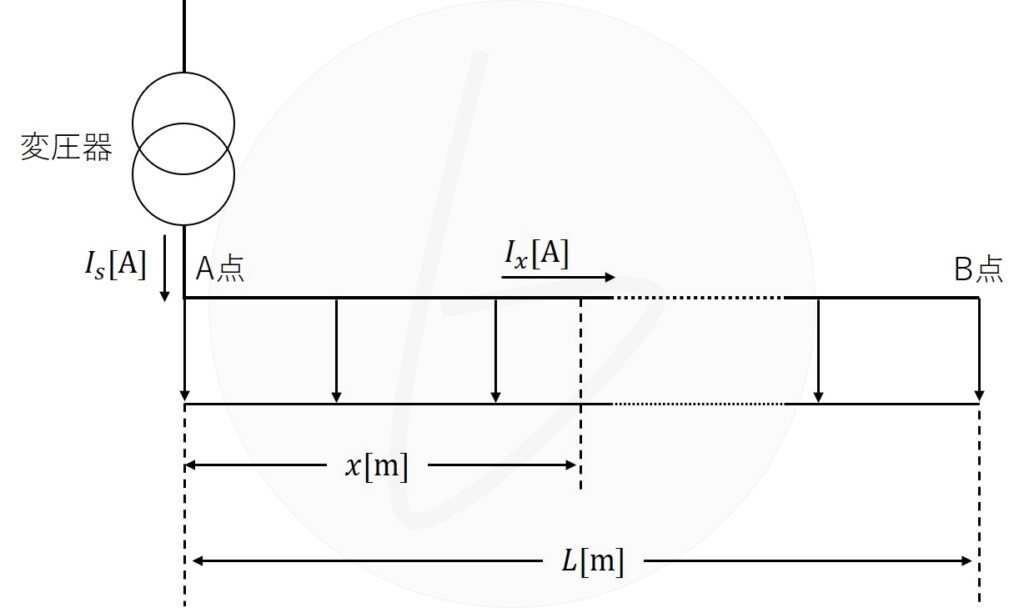
図1 平等負荷分布
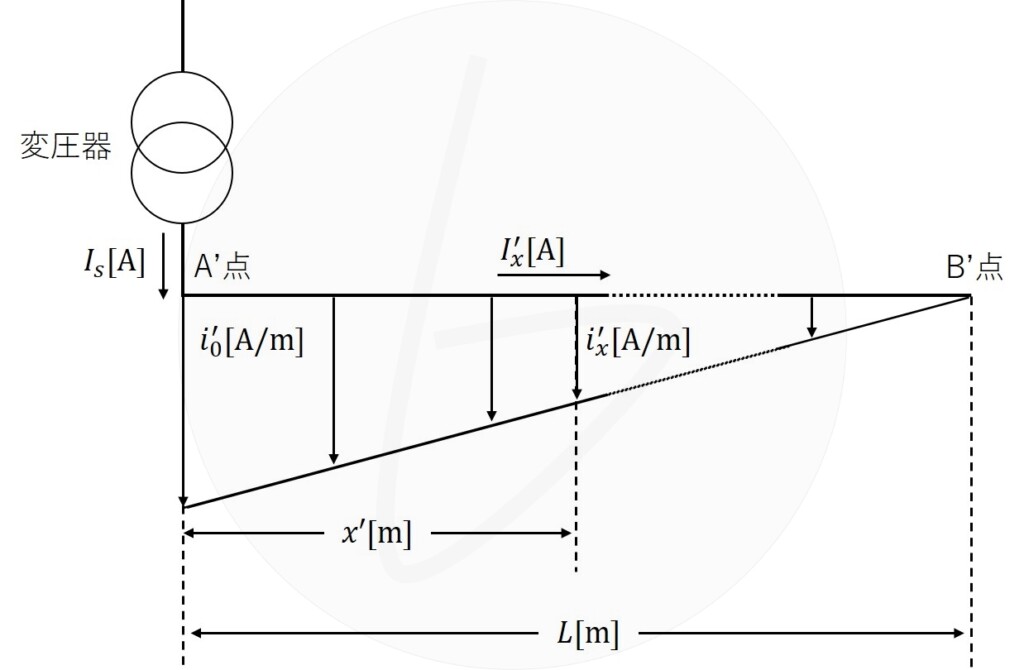
図2 不平等負荷分布
解答・解説
小問(1):電力損失低減策
- 電線を太線化する。
- 回線数を増やす。
- 電圧階級を格上げする。
電線路における電力損失は、$RI^2$です。
そのため、電力損失低減のためには、抵抗Rを小さくするか、電流Iを小さくするかになります。
線路の太線化や回線数の増加は、抵抗$R$が小さくなります。
電圧階級の格上げは、同じ電力を送電する場合においても、$\sqrt{3}VI$より、$V$が大きくなれば$I$が小さくなります。
そのほか、標準回答にあるような力率改善についても、無効電力を減らすことで、電圧と電流の位相差を$0$に近づけ、より小さい電流で同じ有効電力を送電することにつながります。
小問(2):平等負荷及び不平等負荷時の電力損失の計算
a)平等負荷時
平等負荷なので、変圧器から$x\left[{\rm m}\right]$離れた点の負荷電流は、
$$\frac{I_s}{L}\tag{1}$$
である。
地点$x\left[{\rm m}\right]$における線路電流は、地点$x\left[{\rm m}\right]$からB地点までの負荷電流の総和なので、
$$\begin{align}
I_x&=\int_x^L \frac{I_s}{L}dx\\
&=\frac{I_s}{L}\left[x\right]_x^L\\
&=I_s\left(1-\frac{x}{L}\right)\tag{2}
\end{align}$$
となる。
$x\left[{\rm m}\right]$の地点における微小長さ$dx$で生じる電力損失$dW_{1x}$は
$$\begin{align}
dW_{1x}&=rI_x^2dx\\
&=r\left\{I_s\left(1-\frac{x}{L}\right)\right\}^2dx\tag{3}
\end{align}$$
であるから、これを$0$~$L$で積分して、
$$\begin{align}
W_{1x}&=\int_{0}^{L}{dW_{1x}}\\
&=\int_{0}^{L}{r\left\{I_s\left(1-\frac{x}{L}\right)\right\}^2}dx\\
&=rI_s^2\int_{0}^{L}\left(1-2\frac{x}{L}+\left(\frac{x}{L}\right)^2\right)dx\\
&=rI_s^2\left[x-\frac{x^2}{L}+\frac{x^3}{3L^2}\right]_0^L\\
&=rI_s^2\left(L-L+\frac{1}{3}L\right)\\
&=\frac{1}{3}LrI_s^2\tag{4}
\end{align}$$
となる。
ここで、単相2線式なので、2線分の電力損失として2倍する必要があり、
$$W_{2x}=\frac{2}{3}LrI_s^2\tag{5}$$
となる。
(答)線路電流:$I_x=I_s\left(1-\frac{x}{L}\right)$、電力損失:$\frac{2}{3}LrI_s^2$
2倍するのは忘れやすいので注意してください。もしも三相3線であれば3倍です。
b)不平等負荷時
$x=0\left[{\rm m}\right]$において負荷電流密度は$i_0’\left[{\rm A}\right]$、$x=L\left[{\rm m}\right]$において負荷電流密度は$0\left[{\rm A}\right]$であるので、$i_x’$は、
$$i_x’=\frac{i_0’}{L}\left(L-x’\right)\tag{6}$$
となる。
地点$x\left[{\rm m}\right]$における線路電流$I_x’$は、地点$x’\left[{\rm m}\right]$からB地点までの負荷電流の総和なので、$i_x’$を$x’,$~$L$で積分して、
$$\begin{align}
I_x’&=\int_{x’}^{L} i_x’dx’\\
&=\int_{x’}^{L} \frac{i_0’}{L}\left(L-x’\right)dx’\\
&=\frac{i_0′}{L}\left[Lx’-\frac{x’^2}{2}\right]_{x’}^{L}\\
&=\frac{i_0′}{L}\left\{L\left(L-x’\right)-\frac{1}{2}\left(L^2-x’^2\right)\right\}\\
&=\frac{i_0’}{2L}\left(L^2-2Lx’+x’2\right)\\
&=\frac{i_0’}{2L}\left(L-x’\right)^2\tag{7}
\end{align}$$
となる。
$x’\left[{\rm m}\right]$の地点における微小長さ$dx’$で生じる電力損失$dW_{1x’}$は
$$\begin{align}
dW_{1x’}&=rI_x^2dx’\\
&=r\left\{\frac{i_0’}{2L}\left(L-x’\right)^2\right\}^2dx’\tag{8}
\end{align}$$
であるから、これを$0$~$L$で積分して、
$$\begin{align}
W_{1x’}&=\int_0^L r\left\{\frac{i_0’}{2L}\left(L-x’\right)^2\right\}^2dx’\\
&=r\frac{i_0’^2}{4L^2}\left[\frac{1}{5}\left(L-x’\right)^5・\left(-1\right)\right]_0^L\\
&=\frac{ri_0’^2}{20}L^3\tag{9}
\end{align}$$
となり、単相2線式なので2倍して、電力損失は、
$$\begin{align}
W_{2x’}&=2W_{1x’}\\
&=\frac{ri_0’^2}{10}L^3\tag{10}
\end{align}$$
となる。
なお、$I_s$は$I_x’$の$x’=0$の値であるので、
$$\begin{align}
I_s&=I_x’|_{x’=0}\\
&=\frac{i_0’}{2}L\tag{11}
\end{align}$$
$$i_0’=\frac{2}{L}I_s\tag{12}$$
なので、式(9)に代入してi_0’を消去すれば、
$$\begin{align}
W_{2x’}&=\frac{r’}{10}L^3\left(\frac{2}{L}I_s\right)^2\\
&=\frac{2}{5}r’LI_s^2\tag{13}
\end{align}$$
となる。
(答)負荷電流密度:$i_x’=\frac{i_0’}{L}\left(L-x’\right)$、線路電流:$I_x’=\frac{i_0’}{2L}\left(L-x’\right)^2$、電力損失:$\frac{2}{5}LrI_s^2$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。





