みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
この記事では、平成30年度 電験2種 2次試験 電力・管理 問3の過去問解説をします。
電力円線図(送電円・受電円)の問題で、難易度は高めです。
電験2種を受験する際に、電力円線図について対策している方はそこまで多くないと思いますので、この問題を通して、電力円線図が何なのかを理解しておけばOKと思います。
参考に、公開されている過去問(平成21年度まで)を見ても、再び電験2種で電力円線図が出題される可能性は低いと思います。
しかし、絶対出題されないわけではないので、本問のような代表的な良問1問の解き方をマスターしておけば、試験当日になんとかできるでしょう。
平成30年度 電験2種 2次試験 電力・管理 問3 問題文
電力円線図と無効電力損失に関して、次の問に答えよ。ただし、計算には全て単位法を用いること。
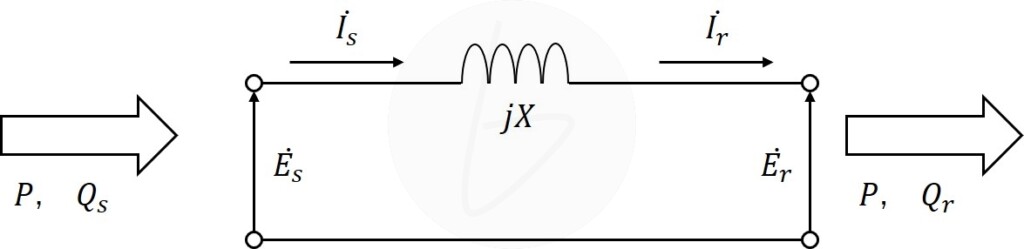
(1)短距離の高圧送電線は、対地容量と線路抵抗を無視すると図のような等価回路で表現できる。送受電端の電圧の大きさがともに$1.0{\rm p.u.}$に保たれるとして、送電電力$P$、送電端無効電力$Q_s$、受電端無効電力$Q_r$はそれぞれどのように表されるか。送受電端電圧間の位相差$\delta$(受電端を基準とする)と送電線リアクタンス$X$を用いて表せ。ただし、無効電力は遅れを正とする。
(2)上記の場合に、送電端複素電力$\dot{S_s}=P+jQ_s$及び受電端複素電力$\dot{S_r}=P+jQ_r$が複素平面上で円を描くことを示せ。
(3)上で求めた二円はそれぞれ送電円、受電円と呼ばれており、一般に複素平面上に表された複素送電電力の線図を電力円線図と呼ぶ。送電線の亘長が2倍になり、$X$が2倍になっても引き続き同一の有効電力を送電する場合、$\delta$が大きく開くことを送電円を用いて説明せよ。
(4)(3)に記したように$X$を2倍にした送電線でも同一の有効電力を送電するとき、無効電力損失が$X$を2倍にする前と比べてどうなるかを送電円、受電円を用いて説明せよ。
(5)周波数$50{\rm Hz}$、作用インダクタンス$1.3{\rm mH/km}$をもつ$10{\rm km}$一回線の送電線で$300{\rm MW}$を送電する場合について送電円、受電円を描き、$sin\delta$と無効電力損失$Q_s-Q_r$を算出せよ。単位法は基準電圧$66{\rm kV}$、基準容量$1 000{\rm MV・A}$とし、$\pi=3.1416$とする。
解答・解説
小問(1)送電電力・送電端無効電力・受電端無効電力の計算
頻繁に登場する送電線を流れる電力の計算です。類題として、令和元年度 問2、令和4年度 問3があります。

問題図では、送電端の電流$\dot{I_s}$と受電端の電流$\dot{I_r}$が別々に描かれていますが、電流の流出経路がないので、
$$\dot{I}=\dot{I_s}=\dot{I_r}$$
となります。
※もし、仮に対地静電容量を考慮し、コンデンサが接続されたT形等価回路やπ型等価回路であれば、$\dot{I_s}$と$\dot{I_r}$は異なります。
送電線のベクトル図より、
$$\dot{E_s}=\dot{E_r}+jX\dot{I}\tag{1}$$
であるから、送電線を流れる電流は、
$$\dot{I}=\frac{\dot{E_s}-\dot{E_r}}{jX}\tag{2}$$
となる。
送電端の皮相電力$\dot{S_s}$は、
$$\begin{align}
\dot{S_s}&=\dot{E_s} \dot{I}^*\\
&=\dot{E_s}\left(\frac{\dot{E_s}-\dot{E_r}}{jX}\right)^*\\
&=\dot{E_s}\left(\frac{\dot{E_s}^*-\dot{E_r}*}{-jX}\right)\\
&=\frac{\dot{E_s} \dot{E_s}^*-\dot{E_s} \dot{E_r}^*}{-jX}\\
&=\frac{E_s^2-\dot{E_s} \dot{E_r}^*}{-jX}\tag{3}
\end{align}$$
ここで、
$$\begin{cases}
\dot{E_r}=E_r\\
\dot{E_s}=Escos\delta+jsin\delta
\end{cases}\tag{4}$$
であるから、
$$\begin{align}
\dot{S_s}&=\frac{E_s^2-E_rE_s\left(cos\delta+jsin\delta\right)}{-jX}\\
&=\frac{E_rE_s}{X}sin\delta+j\frac{E_s\left(E_s-E_rcos\delta\right)}{X}\tag{5}
\end{align}$$
よって、送電端の有効電力$P_S$と無効電力$Q_s$は、
$$\begin{cases}
P_s=Re\left[\dot{S_s}\right]=\frac{E_rE_s}{X}sin\delta\\
Q_s=Im\left[\dot{S_s}\right]=\frac{E_s\left(E_s-E_rcos\delta\right)}{X}
\end{cases}\tag{6}$$
となる。
次に受電端の皮相電力$\dot{S_r}$は、
$$\begin{align}
\dot{S_r}&=\dot{E_r}\dot{I}^*\\
&=\dot{E_r}\left(\frac{\dot{E_s}-\dot{E_r}}{jX}\right)^*\\
&=\dot{E_r}\left(\frac{\dot{E_s^*}-\dot{E_r^*}}{-jX}\right)\\
&=\frac{\dot{E_r}\dot{E_s^*}-\dot{E_r}\dot{E_r^*}}{-jX}\\
&=\frac{E_rE_s\left(cos\delta-jsin\delta\right)-E_r^2}{-jX}\\
&=\frac{E_rE_s}{X}sin\delta+j\frac{E_r\left(E_scos\delta-E_r\right)}{X}\tag{7}
\end{align}$$
よって、受電端の有効電力$P_r$と無効電力$Q_r$は、
$$\begin{cases}
P_r=Re\left[\dot{S_r}\right]=\frac{E_rE_s}{X}sin\delta\\
Q_r=Im\left[\dot{S_r}\right]=\frac{E_r\left(E_scos\delta-E_r\right)}{X}
\end{cases}\tag{8}$$
となる。
以上より、$E_s=E_r=1\left[{\rm p.u.}\right]$を代入して、
$$\begin{cases}
P=P_s=P_r=\frac{E_rE_s}{X}sin\delta=\frac{sin\delta}{X}\\
Q_s=\frac{E_s\left(E_s-E_rcos\delta\right)}{X}=\frac{1-cos\delta}{X}\\
Q_r=\frac{E_r\left(E_scos\delta-E_r\right)}{X}=\frac{cos\delta-1}{X}
\end{cases}\tag{9}$$
となる。
(答)送電電力$P=\frac{sin\delta}{X}$、送電端無効電力$Q_s=\frac{1-cos\delta}{X}$、受電端無効電力$Q_r=\frac{cos\delta-1}{X}$
参考に、送電線にあるインダクタ$X$が消費する遅れ無効電力$Q_L$を計算してみます。
まず、インダクタが消費する皮相電力$\dot{S_L}$は、
$$\begin{align}
\dot{S_L}&=\left(\dot{E_s}-\dot{E_r}\right)\dot{I^*}\\
&=\left(\dot{E_s}-\dot{E_r}\right)\left(\frac{\dot{E_s}-\dot{E_r}}{jX}\right)^*\\
&=\left(\dot{E_s}-\dot{E_r}\right)\left(\frac{\dot{E_s^*}-\dot{E_r^*}}{-jX}\right)\\
&=\frac{\dot{E_s}\dot{E_s^*}-\dot{E_s}\dot{E_r^*}-\dot{E_r}\dot{E_s^*}+\dot{E_r}\dot{E_r^*}}{-jX}\\
&=\frac{E_s^2+E_r^2-E_rE_s\left(cos\delta+jsin\delta\right)-E_rE_s\left(cos\delta-jsin\delta\right)}{-jX}\\
&=\frac{E_s^2+E_r^2-2E_rE_scos\delta}{-jX}\\
&=j\frac{E_s^2+E_r^2-2E_rE_scos\delta}{X}
\end{align}$$
よって、インダクタが消費する遅れ無効電力$Q_L$は、
$$\begin{align}
Q_L&=Im\left[\dot{S_L}\right]\\
&=\frac{E_s^2+E_r^2-2E_rE_scos\delta}{X}
\end{align}$$
となります。
では、送電端の無効電力と受電端の無効電力の差分を計算してみると、
$$\begin{align}
Q_s-Q_r&=\frac{E_s\left(E_s-E_rcos\delta\right)}{X}-\frac{E_r\left(E_scos\delta-E_r\right)}{X}\\
&=\frac{E_s^2+E_r^2-2E_rE_scos\delta}{X}
\end{align}$$
となって、$Q_L$と同じ値になることが確認できます。
また、インダクタの皮相電力$\dot{S_L}$において、$\dot{S_L}$が実部を持たないため、インダクタが有効電力を消費しないことがわかります。
小問(2)電力円線図の導出
送電円の導出
まずは送電端皮相電力について、
$$\begin{align}
\dot{S_s}&=\frac{E_rE_s}{X}sin\delta+j\frac{E_s\left(E_s-E_rcos\delta\right)}{X}\\
&=\frac{sin\delta}{X}+j\frac{1-cos\delta}{X}\tag{10}
\end{align}$$
であり、実部$x$、虚部$y$とおけば、
$$\begin{cases}
x=\frac{sin\delta}{X}\\
y=\frac{1-cos\delta}{X}
\end{cases}\tag{11}$$
であるから、
$$\begin{cases}
sin\delta=Xx\\
cos\delta=1-Xy
\end{cases}\tag{12}$$
となる。
$$sin^2 \delta+cos^2 \delta=1\tag{13}$$
であるから、
$$\left(Xx\right)^2+\left(1-Xy\right)^2=1\tag{14}$$
$$x^2+\left(y-\frac{1}{X}\right)^2=\frac{1}{X^2}\tag{15}$$
となる。
よって、中心($0$, $\frac{1}{X}$)、半径$\frac{1}{X}$の円になる。
受電円の導出
次に受電端皮相電力について、
$$\begin{cases}
x=\frac{sin\delta}{X}\\
y=\frac{cos\delta-1}{X}
\end{cases}\tag{16}$$
であるから、
$$\begin{cases}
sin\delta=Xx\\
cos\delta=1+Xy
\end{cases}\tag{17}$$
$$\left(Xx\right)^2+\left(1+Xy\right)^2=1\tag{18}$$
$$x^2+\left(y+\frac{1}{X}\right)^2=\frac{1}{X^2}\tag{19}$$
よって、中心($0$, $-\frac{1}{X}$)、半径$\frac{1}{X}$の円になる。
(答)送電端:中心($0$, $\frac{1}{X}$)、半径$\frac{1}{X}$の円、受電端:中心($0$, $-\frac{1}{X}$)、半径$\frac{1}{X}$の円
小問(3)送電線リアクタンスの増加と相差角の関係性の図解
電力円線図を描くと、解図1の通りになる。

解図1
送電円について、式(12)から$tan\delta$を計算すれば、
$$\begin{align}
tan\delta&=\frac{Xx}{1-Xy}\\
&=\frac{x}{\frac{1}{X}-y}\tag{20}
\end{align}$$
となる。
そのため、送電円においての$\delta$は、解図2の通りとなる。
ここでポイントですが、解図2において赤点で示している送電円上の座標は($x$, $y$)であり、送電円の中心の$y$座標が$\frac{1}{X}$であるため、式(20)で示している$tan\delta$の条件を満たしていることになります。
$\delta$について、安定限界となるのは$\frac{\pi}{2}$であり、電力系統が安定して送電を継続するには、$\delta≦\frac{\pi}{2}$である必要がある。
そのため、解図3に示す通り、送電円の上半分については不安定点となるので、ここでは下半分のみを考えることとする。

解図2

(a)電力円線図の$\delta$ |

(b)電力円線図の安定領域と不安定領域 |
解図3
長距離送電によって、$X$が$2X$になったときの電力円線図を解図4に示す。
解図4において送電円に着目すると、リアクタンスが大きくなり、送電円が小さくなれば、同じ有効電力を送電する場合の$\delta$の値が大きくなることがわかる。
式(11)及び式(16)から、$x$座標は有効電力$P$そのものを示していることを思い出してください。

解図4
小問(4)送電線のリアクタンス増加に伴う無効電力損失変動の図解
解図5に示す通り、送電円と受電円の動作点において、無効電力の差(虚軸の値の差)は、$X$が大きい時ほど離れるため、長距離送電となり$X$の値が大きくなるほど、無効電力損失は大きくなる。

解図5
送電円は式(11)から、
- $x$座標:送電端の有効電力
- $y$座標:送電端の無効電力
であり、受電円は式(16)から、
- $x$座標:受電端の有効電力
- $y$座標:受電端の無効電力
と定義されています。
また、小問(1)の結果から、送電線には損失がないため、送電端・受電端における有効電力$P$の値は同じです。そのため、送電円・受電円ともに、同じ$x$座標の値を比較することになります。
そして、同じ$x$座標における送電円・受電円の$y$座標の値がそれぞれ送電端の無効電力、受電端の無効電力を示しているので、この差が大きいほど、言い換えればグラフ上で距離が離れているほど、無効電力の損失が大きくなることを示しています。
解図5から明らかなように、リアクタンスが大きくなれば同じ有効電力$P$($x$座標)を送電する場合の無効電力損失(送電円・受電円の距離)が大きくなることがわかります。
小問(5)相差角と無効電力損失の具体的計算
送電線のリアクタンス$X\left[{\rm Ω}\right]$は、(題意より$\pi=3.1416$であることに注意)
$$\begin{align}
X&=2\pi×50×1.3×10^{-3}×10\\
&=4.08408\left[{\rm Ω}\right]\tag{21}
\end{align}$$
単位法の基準容量$S_{BASE}=1000\left[{\rm MV・A}\right]$、基準電圧$V_{BASE}=66\left[{\rm kV}\right]$なので、基準電流$I_{BASE}$は、
$$\begin{align}
I_{BASE}&=\frac{S_{BASE}}{3×\frac{V_{BASE}}{\sqrt{3}}}\\
&=\frac{1000×10^6}{3×\frac{66×10^3}{\sqrt{3}}}\\
&=8747.47474746\left[{\rm A}\right]\tag{22}
\end{align}$$
よって、基準インピーダンス$Z_{BASE}$は、
$$\begin{align}
Z_{BASE}&=\frac{\frac{V_{BASE}}{\sqrt{3}}}{I_{BASE}}\\
&=\frac{\frac{66×10^3}{\sqrt{3}}}{8747.47474746}\\
&=4.35625556699\left[{\rm Ω}\right]\tag{23}
\end{align}$$
よって、線路リアクタンス$X$を単位法$\left[{\rm p.u.}\right]$に直すと、
$$\begin{align}
X=\frac{4.08408}{4.35625556699}\\
&=0.93752075313\left[{\rm p.u.}\right]\tag{24}
\end{align}$$
となる。
送電円を示す関数は、
$$x^2+\left(y-\frac{1}{0.93752075313}\right)^2=\frac{1}{0.93752075313^2}\tag{25}$$
であるから、
$$x^2+\left(y-1.06664305473\right)^2=1.06664305473^2\tag{26}$$
となり、中心($0$, $1.07$)、半径$1.07$の円となる。
同様に、受電円を示す関数は、
$$x^2+\left(y+\frac{1}{0.93752075313}\right)^2=\frac{1}{0.93752075313^2}\tag{27}$$
であるから、
$$x^2+\left(y+1.06664305473\right)^2=1.06664305473^2\tag{28}$$
となり、中心($0$, $-1.07$)、半径$1.07$の円となる。
送電する有効電力は$P=300\left[{\rm MW}\right]$であり、単位法に直せば$P=0.3\left[{\rm p.u.}\right]$である。
送電円において$x=0.3$となる$y$の値は、
$$0.3^2+\left(y-1.06664305473\right)^2=1.06664305473^2\tag{29}$$
$$y=\begin{cases}
0.04305749104\\
2.09022861842
\end{cases}\tag{30}$$
であり、安定性の観点から送電円の下半分を見るため$y≦1.07$だから、
$$\begin{align}
Q_s&=y\\
&=0.04305749104\tag{31}
\end{align}$$
となる。
同様に、受電円において$x=0.3$となる$y$の値は、
$$0.3^2+\left(y+1.06664305473\right)^2=1.06664305473^2\tag{32}$$
$$y=\begin{cases}
-0.04305749104\\
-2.09022861842
\end{cases}\tag{33}$$
であり、安定性の観点から送電円の上半分を見るため$y≧-1.07$だから、
$$\begin{align}
Q_r&=y\\
&=-0.04305749104\tag{34}
\end{align}$$
となる。
電力円線図で示すと、解図6の通りになる。

解図6
以上より、$sin\delta$は、解図において赤で塗った三角形で計算できて、
$$\begin{align}
sin\delta&=\frac{P}{\frac{1}{X}}\\
&=\frac{0.3}{1.06664305473}\\
&=0.28125622594\tag{35}
\end{align}$$
となる。
無効電力損失は、
$$\begin{align}
Q_s-Q_r&=0.04305749104-\left(-0.04305749104\right)\\
&=0.08611498208\tag{36}
\end{align}$$
となる。
(答)$sin\delta=0.281$、無効電力損失$0.0861\left[{\rm p.u.}\right]$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。





