みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
この記事では、平成29年度 電験2種 2次試験 電力・管理 問3の過去問解説をします。
この問題は、単位法を用いて短絡容量や電圧変動を計算する基本的な問題です。
一見ややこしそうに見えますが、順に解いていけば必ず解ける問題になっているので、知識の確認の意味も含めて解いてみてください。
平成29年度 電験2種 二次試験 電力・管理 問3 問題文
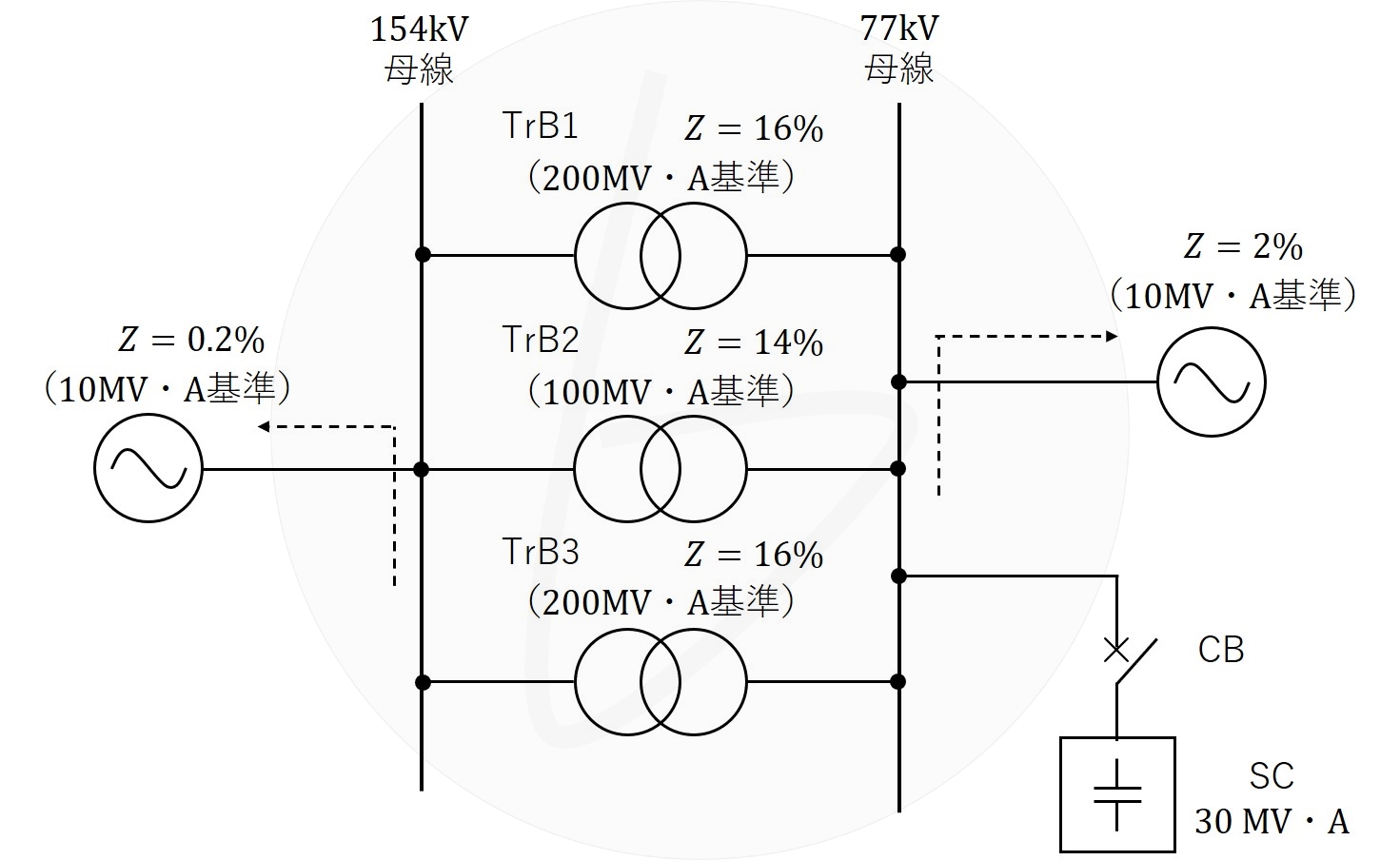
図のような一次側が$154{\rm kV}$、二次側が$77{\rm kV}$の変圧器3台で連系された変電所がある。この変電所の$77{\rm kV}$側母線に接続された$30{\rm MV・A}$の電力用コンデンサを投入したとき、次の問に答えよ。なお、各変圧器のインピーダンスはリアクタンスのみとし、その値は自己容量基準で図に示すとおりである。
(1)$77{\rm kV}$母線の短絡容量$P_s\left[{\rm MV・A}\right]$を求めよ。なお、単位法における基準容量は$100{\rm MV・A}$とする。
(2)電力用コンデンサを投入したときの$77{\rm kV}$側母線の基準電圧に対する電圧変動率$\Delta V_{77}\left[\%\right]$を求めよ。
(3)電力用コンデンサを投入したときの$154{\rm kV}$側母線の基準電圧に対する電圧変動率$\Delta V_{154}\left[\%\right]$を求めよ。
解答・解説
小問(1)
送電線各部のパーセントインピーダンスを$100{\rm MV・A}$基準にすると、解図1の通りになる。

解図1
$77{\rm kV}$母線から電源側を見たときのパーセントインピーダンスは、赤矢印の方向で、
$$\frac{1}{\frac{1}{8}+\frac{1}{14}+\frac{1}{8}}+2=5.11111111119\left[\%\right]\tag{1}$$
青矢印の方向で、$20\%$である。
これらの並列接続なので、
$$\frac{1}{\frac{1}{5.11111111119}+\frac{1}{20}}=4.07079646022\left[\%\right]\tag{2}$$
短絡比は、パーセントインピーダンス($\left[{\rm p.u.}\right]$値)の逆数なので、
$$\frac{100}{4.07079646022}=24.565217391\tag{3}$$
よって、短絡容量は基準容量の短絡比倍になるので、
$$24.565217391×100\left[{\rm MV・A}\right]=2456.5217391\left[{\rm MV・A}\right]\tag{4}$$
となる。
(答)$2.46×10^3\left[{\rm MV・A}\right]$
小問(2)
$77{\rm kV}$母線から電源側を見たときのインピーダンスを$Z$とすると、小問4より
$$Z=4.07079646022\left[\%\right]\tag{5}$$
である。
コンデンサ容量は$77{\rm kV}$($=1{\rm p.u.}$)$30{\rm MV・A}$($=0.3{\rm p.u.}$)であり電流は$0.3{\rm p.u.}$流れる。
電流経路は解図2の通り。

解図2
この時の電圧変動は、
$$0.3×\frac{4.07079646022}{100}=0.01221238938\left[{\rm p.u.}\right]\tag{6}$$
となる。
母線電圧$1\left[{\rm p.u.}\right]$を基準に電圧変動率を求めると、
$$\frac{1.22123893806}{1}×100=1.221238938\left[\%\right]\tag{7}$$
となる。
(答)$1.22\left[\%\right]$
試験センターの標準回答は、一度${\rm V}$などの単位に直してから計算しています。
試験当日は、慣れた計算法で解いてください。
試験対策という意味では、単位法に苦手意識を持つ方が多いようです。
そこで、この問題は単位法で電圧変動率を計算してみて、単位法そのものに慣れる練習をしておくのもいいでしょう。
(3)
コンデンサに流入する電流Iは、解図3のように$I_1$、$I_2$の経路に分かれて供給される。

解図3
ここで、$I=0.3\left[{\rm p.u.}\right]$を供給する割合は、電流$I_1$、$I_2$のそれぞれの電流経路におけるインピーダンスの逆比で決定するので、電流経路におけるインピーダンス(%値)を計算する。
まず、電流$I_1$の経路のインピーダンスZ_1は、
$$\begin{align}
Z_1&=2+3.11111111119\\
&=5.11111111119\left[\%\right]\tag{8}
\end{align}$$
電流$I_2$の経路のインピーダンス$Z_2$は、
$$Z_2=20\left[\%\right]\tag{9}$$
よって、
$$\begin{align}
I_1&=\frac{Z_2}{Z_1+Z_2}I\\
&=\frac{20}{20+5.11111111119}×0.3\\
&=0.23893805304\left[{\rm p.u.}\right]\tag{10}
\end{align}$$
になる。
この電流$I_1$が流れることで、解図3に示す通り電源と$154{\rm kV}$母線の間のリアクタンスによって電圧降下が発生するので、コンデンサを接続すると、
$$\begin{align}
0.02×I_1&=0.02×0.23893805304\\
&=0.00477876106\left[{\rm p.u.}\right]\tag{11}
\end{align}$$
だけ電圧が低下する。
基準電圧が$1\left[{\rm p.u.}\right]$なので、電圧変動率は、
$$\frac{0.00477876106}{1}×100=0.477876106\left[\%\right]\tag{12}$$
となる。
(答)$0.478\left[\%\right]$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






