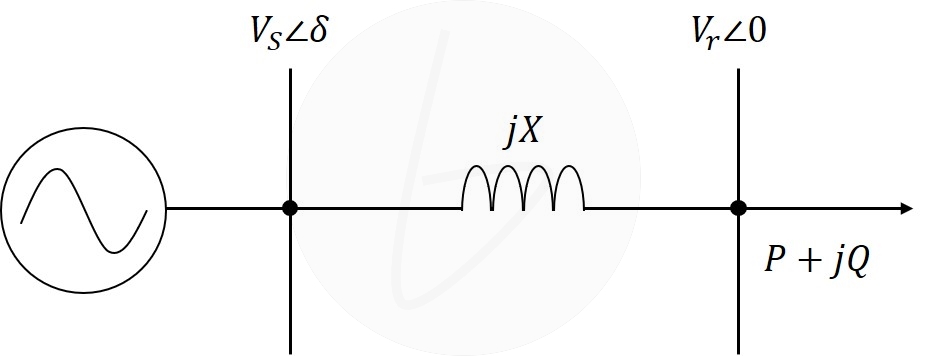
図に示すように、発電機より直列リアクタンス$X$をもつ送電線を介して負荷に有効電力$P$、無効電力$Q$を供給している場合を考える。ここに送電端電圧を$V_S\angle\delta$、受電端(負荷端)電圧を$V_r\angle0$とする。また、無効電力の符号は遅れ無効電力を正とする。
(1)負荷の有効電力$P$及び無効電力$Q$を、$V_S$、$V_r$、$\delta$及び$X$で表す式を導出せよ。
(2)送電端電圧の大きさ$V_S$を$1{\rm p.u.}$、送電線から負荷に供給する有効電力$P$を$0.5{\rm p.u.}$、無効電力$Q$を$0{\rm p.u.}$とするとき、受電端電圧の大きさ$V_r$及び$\delta$($0°≦\delta<45°$)を求めたい。ここに送電線のリアクタンス$X$は0.5p.u.とする。
a)有効電力に関する式から$V_r$を、$\delta$を用いて表せ。
b)無効電力に関する式から$V_r$を、$\delta$を用いて表せ。
c) a)及びb)の結果から$\delta$及び$V_r$の値を求めよ。
ただし、$sin\ 2x=2sin\ x\ cos\ x$、$cos\ 2x=2cos^2x-1$を用いてもよい。
解答・解説
小問(1)
送配電線の有効電力の話が出てきたときは、すぐに下図のベクトル図を思い出してください。
導出過程はワンパターンですし、電験2種では定番の問題なので、確実に慣れておくことも重要です。

なお、基準位相については問題ごとに異なる場合があるので、その都度確認してください。
例えば、令和4年度 問3のように通常とは異なる位相の定義で計算する場合もあります。しかし、それでも回路図に沿ってベクトル図を描けば解けるので、基本を理解しておけばワンパターンな回答で対処できます。
送電端電圧$\dot{V_s}$と受電端電圧$\dot{V_r}$の関係から、
$$\dot{V_s}=\dot{V_r}+jX\dot{I}\tag{1}$$
である。式変形すると、
$$\dot{I}=\frac{\dot{V_s}-\dot{V_r}}{jX}\tag{2}$$
となる。
次に皮相電力について、
$$\begin{align}
\dot{S}&=P+jQ\\
&=\dot{V}\dot{I}^*\\
&=\dot{V_r}\left(\frac{\dot{V_s}-\dot{V_r}}{jX}\right)^*\\
&=\dot{V_r}\left(\frac{\dot{V_s}^*-\dot{V_r}^*}{-jX}\right)\tag{3}
\end{align}$$
となる。
ここで、
$$\begin{cases}
\dot{V_s}=V_s\left(cos\delta+jsin\delta\right)\\
\dot{V_r}=V_r
\end{cases}\tag{4}$$
であるから、共役複素数は、
$$\begin{cases}
\dot{V_s}^*=V_s\left(cos\delta-jsin\delta\right)\\
\dot{V_r}^*=Vr
\end{cases}\tag{5}$$
以上より、
$$\begin{align}
\dot{S}&=V_r\frac{V_s\left(cos\delta-jsin\delta\right)-V_r}{-jX}\\
&=\frac{V_sV_r}{X}sin\delta+j\frac{V_rV_scos\delta-V_r^2}{X}\tag{6}
\end{align}$$
となる。
有効電力$P$、無効電力$Q$について、
$$\begin{cases}
P=Re\left[\dot{S}\right]=\frac{V_sV_r}{X}sin\delta\\
Q=Im\left[\dot{S}\right]=\frac{V_rV_scos\delta-V_r^2}{X}
\end{cases}\tag{7}$$
となる。
(答)$P=\frac{V_sV_r}{X}sin\delta$, $Q=\frac{V_rV_scos\delta-V_r^2}{X}$
小問(2)
a)
$V_s=1\left[{\rm p.u.}\right]$、$P=0.5\left[{\rm p.u.}\right]$、$X=0.5\left[{\rm p.u.}\right]$であるから、式(7)の$P$より、
$$0.5=\frac{1×V_r}{0.5}sin\delta\tag{8}$$
$$V_r=\frac{0.25}{sin\delta}\tag{9}$$
(答)$V_r=\frac{0.25}{sin\delta}$
b)
$Q=0\left[{\rm p.u.}\right]$であるから、式(7)の$Q$より、
$$0=\frac{V_r×1×cos\delta-V_r^2}{0.5}\tag{10}$$
$$Vr=cos\delta\tag{11}$$
(答)$V_r=cos\delta$
c)
小問(2)a), c)の結果から、V_rを消去して、
$$cos\delta=\frac{0.25}{sin\delta}\tag{12}$$
である。
式(12)を整理していくと、
$$2sin\delta cos\delta=0.5\tag{13}$$
$$sin2\delta=0.5\tag{14}$$
$$2\delta=\frac{\pi}{6}\tag{15}$$
$$\delta=\frac{\pi}{12}\tag{16}$$
となる。
また、
$$cos2\delta=2cos^2\delta-1\tag{17}$$
より、
$$cos\frac{\pi}{6}=2cos^2\delta-1\tag{18}$$
$$cos\delta=±0.96592582628\tag{19}$$
よって、小問(2)b)、及び$V_r>0$より、
$$\begin{align}
V_r&=cos\delta\\
&=0.96592582628\tag{20}
\end{align}$$
となる。
(答)$\delta=\frac{\pi}{12}$, $V_r=cos\delta=0.966$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






