この記事では、令和4年度 電験2種 二次試験 電力・管理 問3の過去問解説をします。
送電線により受電する負荷母線の電圧を維持するために必要な調相設備の容量(コンデンサの容量)を求める問題です。
問題の内容としては、電験2種 二次試験レベルとしては標準的ですが、問題設定として、受電端電圧が送電端電圧より進相になっています。
この点において、相差角$\theta_d$が負になるので、注意が必要です。
令和4年度 電験2種 二次試験 電力・管理 問3
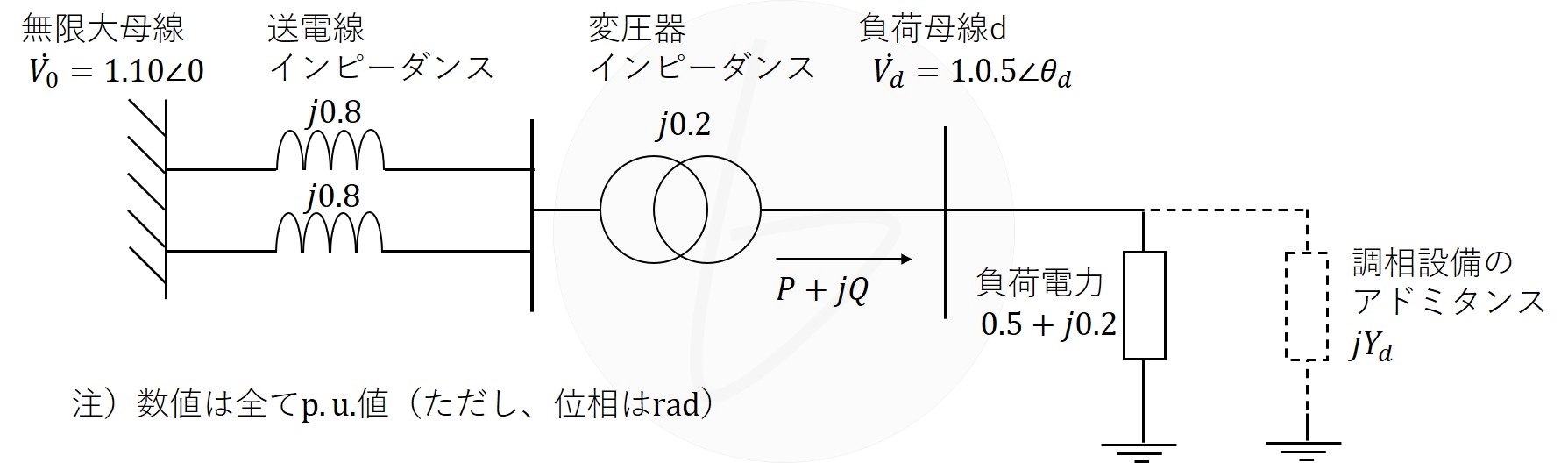
送電線により受電する下図の負荷母線dの受電電圧$V_d$を$1.05{\rm p.u.}$に維持するために必要な調相設備(コンデンサあるいはリアクトル)のサセプタンス$Y_d$を、単位法を用いて、以下の手順で求める。それぞれの問に答えよ。なお、遅れの無効電力を正とする。
(1)負荷母線dに到達する有効電力$P$に関する数式を用いて、$sin\theta_d$の値を求めよ。
(2)負荷母線dに到達する遅れ無効電力$Q$を$cos\theta_d$の関数で表せ。
(3)上記小問(2)の解を用いて必要調相設備サセプタンス$Y_d$を$cos\theta_d$の関数で表せ。
(4)上記の各小問の解を用いて必要調相設備サセプタンス$Y_d$を求めよ。ただし、$\left|\theta_d\right|<\frac{\pi}{2}$とする。
解答・解説
標準回答には記載がありませんが、複素電力を求める式を導出しておきます。
問題設定として、送電端電圧$\dot{V_0}=1.10\angle0$、受電端電圧$\dot{V_d}=1.05\angle\theta_d$となっており、受電端側が進相になっているので符号が面倒ですが、解いていきます。
$$\dot{V_0}-\dot{V_d}=jX\dot{I}$$
$$\begin{align}
\dot{I}&=\frac{\dot{V_0}-\dot{V_d}}{jX}\\
&=\frac{V_0-V_d\left(cos\theta_d+jsin\theta_d\right)}{jX}\\
&=\frac{jV_0-V_d\left(jcos\theta_d-sin\theta_d\right)}{-X}\\
&=-\frac{V_dsin\theta_d}{X}-j\frac{V_0-V_dcos\theta_d}{X}
\end{align}$$
$$\begin{align}
\dot{S}&=\dot{V_d}\dot{I^*}\\
&=V_d\left(cos\theta_d+jsin\theta_d\right)・-\frac{V_dsin\theta_d}{X}+j\frac{V_0-V_dcos\theta_d}{X}\\
&=V_d\left(-\frac{V_d}{X}cos\theta_dsin\theta_d+j\frac{V_0cos\theta_d-V_dcos^2\theta_d}{X}\right.\\
&\left.-j\frac{V_d}{X}sin^2\theta_d-\frac{V_0sin\theta_d-V_dcos\theta_dsin\theta_d}{X}\right)\\
&=-\frac{V_0V_d}{X}sin\theta_d+j\frac{V_d\left(V_0cos\theta_d-V_d\right)}{X}
\end{align}$$
となり、
$$\begin{cases}
P=-\frac{V_0V_d}{X}sin\theta_d\\
Q=\frac{V_d\left(V_0cos\theta_d-V_d\right)}{X}
\end{cases}$$
となります。
有効電力$P$に-符号があることが気になると思いますが、先にも書きましたが、相差角$\theta_d$の定義の方向が、通常考える場合と逆になっているためです。
一般的に相差角$\theta_d$は、電力潮流が送電端→受電端なので、送電端が進相になるように定義します。
今回の問題では相差角$\theta_d$が受電端が進相になるように定義されているので、$\theta_d>0$のときの有効電力の流れは受電端→送電端になります。
そのため、送電端→受電端に送電する場合、$\theta_d<0$となるので、$sin\theta_d<0$となり、もともとのマイナス符号と打ち消しあって、$P>0$となります。
(実際、小問(1)の計算結果は$sin\theta_d<0$となっています。)
本問のベクトル図(受電端電圧が送電端電圧よりも進相)が下図の左の図です。
そして右の図は一般的な図(受電端電圧が送電端よりも遅相)になります。
送電端電圧$\dot{V_0}$、受電端電圧$\dot{V_d}$の位相関係を見ればわかりやすいと思います。
 受電端電圧が送電端電圧よりも進相の時 |
 受電端電圧が送電端電圧より遅相の時 |
小問(1)
有効電力の潮流は、問題に示されているとおり受電端電圧が進相となる向きに$\theta_d$をとると、単位法表記によって、
$$P=-\frac{V_0V_d}{X}sin\theta_d\tag{1}$$
である。
ここで、$X$は、受電端から見た電源側(本問の場合には無限大母線側)のリアクタンスである。またマイナス符号に注意する。
受電端から見た無限大母線側のリアクタンスは、送電線が2回線であることを考慮して、
$$\begin{align}
X&=\frac{0.8}{2}+0.2\\
&=0.6\left[{\rm p.u.}\right]\tag{2}
\end{align}$$
よって、式(1)に、
$$\begin{cases}
P=0.5\\
V_0=1.10\\
V_d=1.05\\
X=0.6\\
\end{cases}\tag{3}$$
を代入して、
$$0.5=-\frac{1.10×1.05}{0.6}×sin\theta_d\tag{4}$$
$$sin\theta_d=-0.25974025973\tag{5}$$
となる。
(答)$sin\theta_d=-0.260$
小問(2)
無効電力の潮流は、
$$Q=\frac{V_d\left(V_0cos\theta_d-V_d\right)}{X}\tag{6}$$
であるから、
$$\begin{align}
Q&=\frac{1.05×\left(1.10cos\theta_d-1.05\right)}{0.6}\\
&=1.925cos\theta_d-1.8375\tag{7}
\end{align}$$
となる。
(答)$Q=1.93cos\theta_d-1.84$
小問(3)
電力系統における受電点の電圧は、下図に示すように、電源から流入する無効電力と受電点で必要とする無効電力の釣り合いによって、受電端電圧が決まります。
本問は、調相設備によって遅れ無効電力を補償することで、受電点の電圧を調整する問題です。

受電端電圧の無効電力は、負荷に必要な無効電力と、調相設備の無効電力の和で決まる。
ここで、調相設備はアドミタンスが進み$jY_d$で定義されているので、コンデンサ、つまり進み無効電力を基準にしていることがわかる。
そのため、調相設備を設置した後に受電端が必要とする無効電力は、遅れ無効電力を正として、
$$\begin{align}
Q&=0.2-Y_d×V_d^2\\
&=0.2-1.1025Y_d\tag{8}
\end{align}$$
よって、
$$1.925cos\theta_d-1.8375=0.2-1.1025Y_d\tag{9}$$
$$Y_d=-1.74603174603cos\theta_d+1.84807256235\tag{10}$$
となる。
(答)$Y_d=-1.75cos\theta_d+1.85$
小問(4)
小問(1)より、$sin\theta_d=-0.25974025973$であるので、
$$\begin{align}
cos\theta_d&=\sqrt{1-sin^2 \theta_d}\\
&=\sqrt{1-\left(-0.25974025973\right)^2}\\
&=0.96567851662\tag{11}
\end{align}$$
となる。
式(10)に代入すれば、
$$\begin{align}
Y_d&=-1.74603174603cos\theta_d+1.84807256235\\
&=-1.74603174603×0.96567851662+1.84807256235\\
&=0.16196721588\tag{12}
\end{align}$$
となる。
(答)$Y_d=0.162$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






