みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
この記事では、令和元年度 電験2種 2次試験 電力・管理 問5の過去問解説をします。
電力系統における無効電力の変化による電圧変動を計算する問題で、難易度としては少し難しめといった感じのレベルです。
一番躓きやすいのが小問(1)b)で、ここさえクリアできれば、それ以外は普通の単位法の計算でしょう。
では、過去問解説をしていきます!
令和元年度 電験2種 2次試験 電力・管理 問5
電力系統における無効電力の変化による電圧変動に関し、次の問に答えよ。なお、各要素と単位は次のとおりとする。
有効電力$P$:$\left[{\rm W}\right]$、無効電力$Q$:$\left[{\rm var}\right]$、送電端電圧$V_S$及び受電端電圧$V_r$:$\left[{\rm V}\right]$、抵抗$r$及びリアクタンス$x$:$\left[{\rm Ω}\right]$
(1)図1は、電源から負荷(遅れ力率)に電力$P+jQ$を送電している状態を示している。次のa)及びb)について答えよ。
a)受電端電圧$V_r$を基準として、1相分の電圧、電流の関係をベクトル図で表せ。ただし、受電端電圧$V_r$及び送電端電圧$V_S$は線間電圧とする。
b)負荷の有効電力$P$、抵抗$r$及びリアクタンス$x$は一定とし、$V_S$と$V_r$の位相差は近似的に零であるとみなした場合、無効電力の変化$\Delta Q$と、それによる受電端電圧の変化$\Delta v$とは、①式の関係があることを証明せよ。ただし、送電端電圧$V_S$は一定とし、受電端電圧$V_r$の変化は小さく、また、$r<<x$とする。
$$\Delta v\propto -x・\Delta Q$$
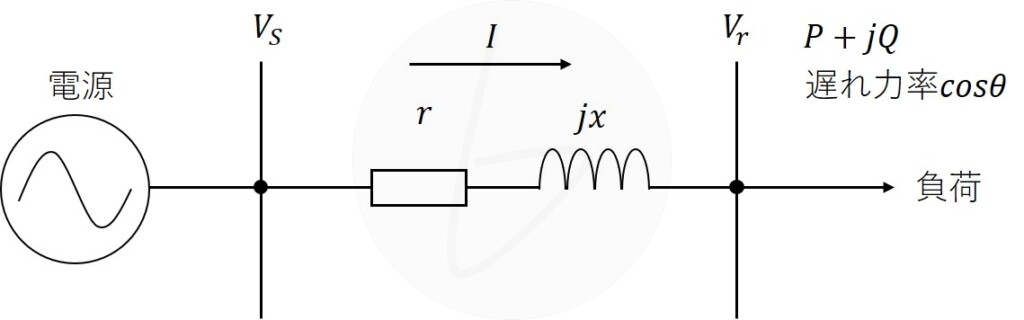
図1
(2)図2は、電源1(商用電源)に電源2(分散電源)が接続された電力系統を示している。$22{\rm kV}$母線に分路リアクトル(ShR)を投入したとき、$22{\rm kV}$母線の電圧変動率を$2\%$以下にするためには、投入する容量$Q_R$は最大何${\rm Mvar}$とすべきか。$1{\rm Mvar}$未満は四捨五入して答えよ。ただし、①式が成立するものとし、$22{\rm kV}$母線の電圧$V_{22}$の送電端電圧$V_S$に対する電圧変化を$v$とすると、$22{\rm kV}$母線の電圧変動率$\%v_{22}$は次式で表されるものとする。
$$\%v_{22}\left[\%\right]=\frac{v}{V_{22}}×100\left[\%\right]$$
また、系統各部のリアクタンスは$10{\rm MV・A}$基準の値とし、電源電圧は変化しないものとする。
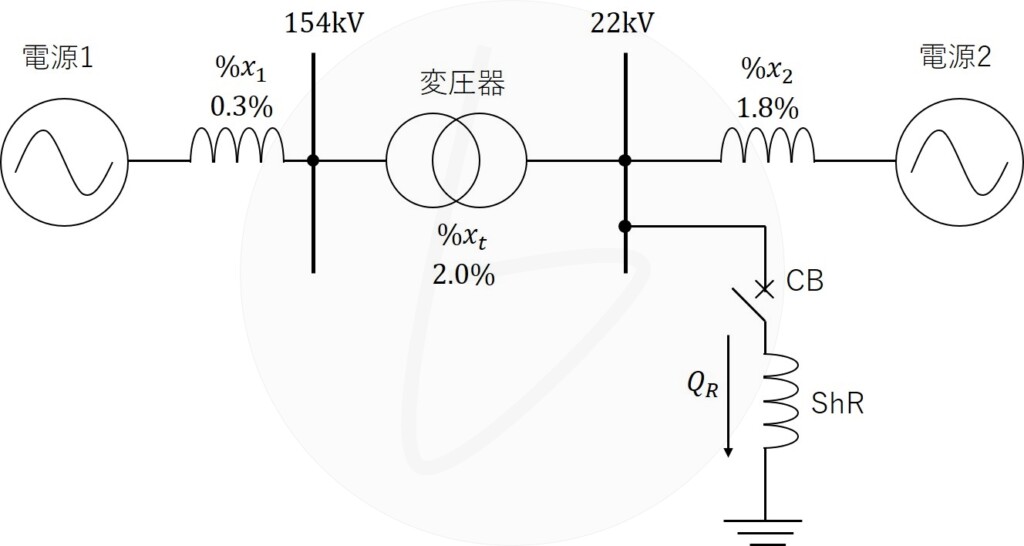
図2
解答・解説
小問(1)
a)ベクトル図の作成
解図1の通りになる。

解図1
(答)解図1の通り。
b)無効電力変化による電圧変動の近似式の導出
解図1のベクトル図より、
$$\frac{\dot{V_s}}{\sqrt{3}}=\frac{\dot{V_r}}{\sqrt{3}}+\left(rcos\theta+Xsin\theta\right)I+j\left(xcos\theta-rsin\theta\right)I\tag{1}$$
である。
ここで、$\dot{V_s}$と$\dot{V_r}$の位相差が非常に小さいため、虚部を無視できて、
$$\frac{V_s}{\sqrt{3}}=\frac{V_r}{\sqrt{3}}+\left(rcos\theta+xsin\theta\right)I\tag{2}$$
$$V_s=V_r+\sqrt{3}\left(rcos\theta+xsin\theta\right)I\tag{3}$$
となる。
ここで、有効電力$P$と無効電力$Q$について、
$$\begin{cases}
P=3VIcos\theta\\
Q=3VIsin\theta
\end{cases}\tag{4}$$
であるから、式(3)に代入して、
$$V_s=V_r+\frac{rP+xQ}{V_r}\tag{5}$$
さらに、$r<<x$より、
$$V_s=V_r+\frac{xQ}{V_r}\tag{6}$$
整理して、
$$V_r=V_s-\frac{xQ}{V_r}\tag{7}$$
となる。ここで、式(7)において$V_s$の微小変化(増加)させ$V_r+\Delta V_r$としたとき、$Q$も微小変化して$Q+\Delta Q$になる。
これより、
$$\begin{align}
V_r+\Delta V_r&=V_s-\frac{x\left(Q+\Delta Q\right)}{V_r}\\
&=V_s-\frac{xQ}{V_r}-\frac{x\Delta Q}{V_r}\tag{8}
\end{align}$$
となる。
式(8)と式(7)より、微小変化分を取り出せば(※補足参照)、
$$\Delta V_r=-\frac{x\Delta Q}{V_r}\tag{9}$$
となり、$V_r$はほぼ一定であるので、$\Delta V$と$x・\Delta Q$は比例する。
以上より、式①が成り立つことを示せた。
式(7)と式(8)から、式(9)に変形するところがわかりにくいと思うので補足です。
下図に示すように、式(7)を使えば、式(8)の基準値に相当する部分が打ち消され、微小変化分だけが残るという計算をしています。

小問(2)母線電圧変動率を抑制する分路リアクトルの容量計算
小問(1)の結果と、問題文で提示された電圧変動率の式より
$$\%v_{22}=\frac{\left|-XQ_R\right|}{V_{22}}×100\tag{10}$$
ここで、$22{\rm kV}$母線から見た電源側のリアクタンスは、
$$\begin{align}
X=\frac{1}{\frac{1}{2+0.3}+\frac{1}{1.8}}\\
&=1.00975609757\left[\%\right]\\
&=0.0100975609757\left[{\rm p.u.}\right]\tag{11}
\end{align}$$
である。
よって、
$$2≧\frac{0.0100975609757Q_R}{1}×100\tag{12}$$
$$Q_R≦1.9806763296\left[{\rm p.u.}\right]\tag{13}$$
となる。この$Q_R$は$10{\rm MVA}$を基準にした単位法表現であり、単位を${\rm MVar}$に直して、
$$\begin{align}
Q_R&=1.9806763296×10\\
&=19.806763296\left[{\rm MVar}\right]\tag{14}
\end{align}$$
$1{\rm MVar}$未満は四捨五入して。
$$Q_R=20\left[{\rm MVar}\right]\tag{15}$$
となる。
(答)$Q_R=20\left[{\rm MVar}\right]$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






