みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
この記事では、
- フィードバック制御の目的
- フィードバック制御の伝達関数の計算公式
について説明しています。
制御理論は抽象的でわかりにくい分野と思われがちですが、身近なフィードバック制御はたくさんありますし、我々自身も日常的にフィードバック制御をしています。
身近な例とともに、フィードバック制御系を説明していきます。
概要:フィードバック制御の要点
フィードバック制御の目的は、、ブロック線図における偏差を0にすることである。
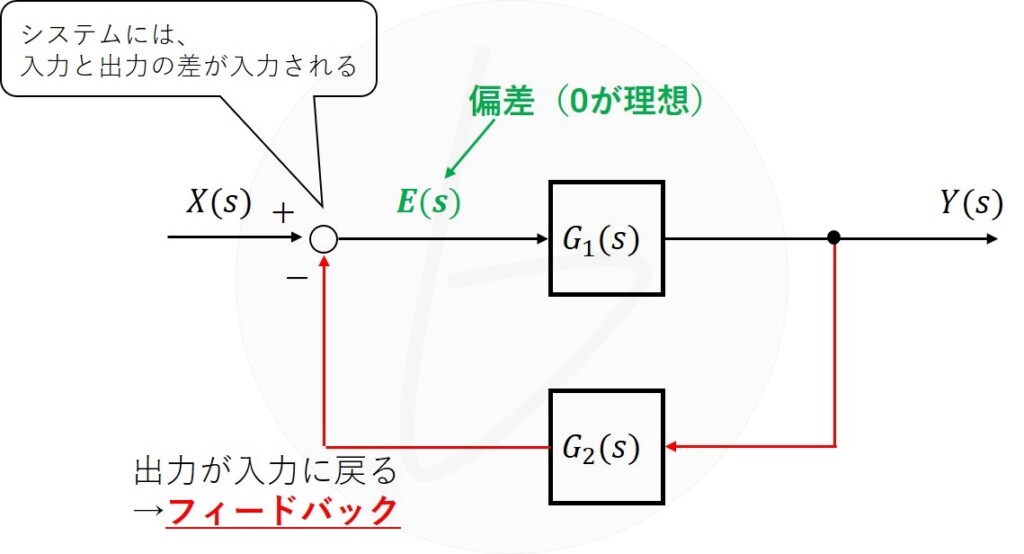
フィードバック制御系のブロック線図は、下図のように、
- $G_1\left(s\right)$:前向き伝達関数
- $G_1\left(s\right)G_2\left(s\right)$:一巡伝達関数
となる。
これらを用いて、フィードバック制御系の伝達関数の公式は、
$$G\left(s\right)=\frac{{\rm 前向き伝達関数}}{1+{\rm 一巡伝達関数}}$$
となる。
フィードバック制御の身近な例と目的
フィードバック制御とは、目標値と出力の差(偏差)を0にすることも目的に行う制御のことを言います。
お風呂の自動湯沸かし機能におけるフィードバック制御の例
日常で考えてみれば、お風呂の自動湯沸かし機能が典型例です。
図2.3.1のように、設定した温度(ここでは40℃)に対して、左図のように湯温が低ければ加熱し、右図のように湯温が高ければ温度を下げる制御(加水や自然放熱による冷却)を行うことで、常に快適な温度を維持しています。
この時の偏差とは、
- お湯の設定温度
- お風呂の実際の温度
の差になります。
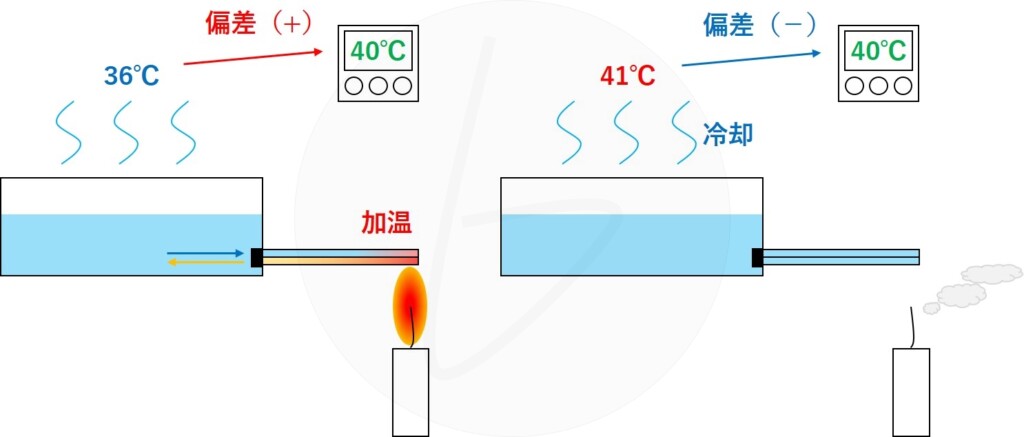
図1 身近なフィードバック制御の例(湯沸かし)
車の運転のフィードバック制御の例
フィードバック制御については、機械だけが行うものではありません。
私たちも、日常生活において、当たり前のようにフィードバック制御を行っているといえます。
例えば車を運転するときを考えてみましょう。
高速道路を走っているとき、制限速度になるまで、アクセルを踏んで加速します。
制限速度に到達したらアクセルを少し緩めます。
その後は上り坂や下り坂など、あらゆる走行状況に応じて制限速度一定で走れるようにアクセルの踏み具合を微調整します。
これがまさに目標値(制限速度)と出力(車速)の偏差を0にしようとするフィードバック制御です。
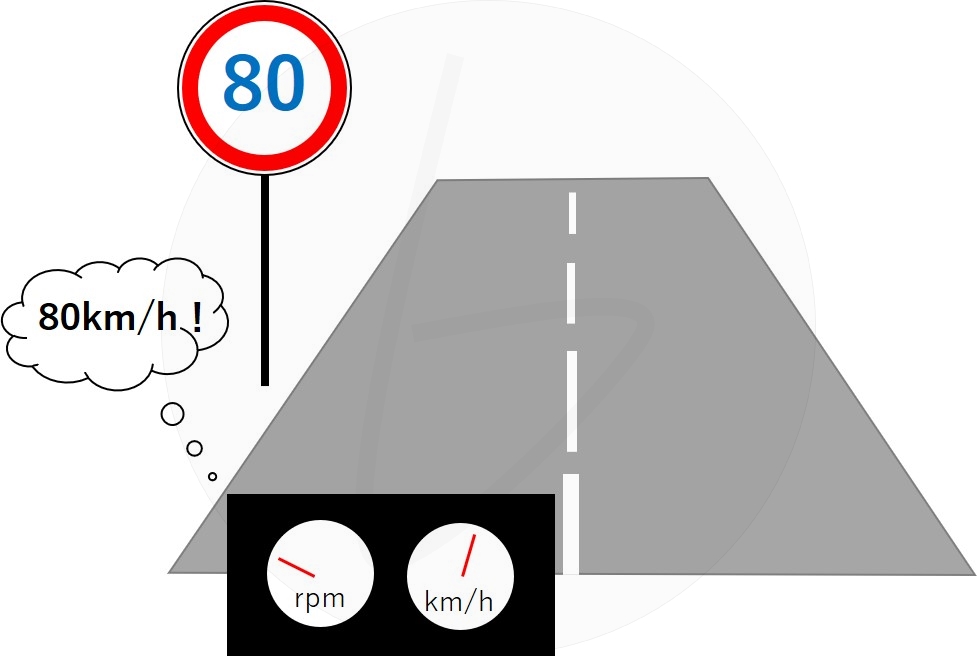
図2 フィードバック制御のイメージ
身近なフィードバック制御
以上のように、フィードバック制御とは、日常のシステムの中に組み込まれているほか、皆さんも日常の生活で無意識のうちに行っている行動です。
自動制御では、こうしたフィードバック動作を、ブロック線図で考え、伝達関数にすることで、システムの応答、具体的には、
- どれぐらいの速度で応答できるか
- オーバーシュートはどの程度か
- どの程度の精度(偏差)なら許容できるか
といったことや、「そもそも暴走しないか?」といったことを考えていくことがメインとなる分野です。
フィードバック制御系のブロック線図
フィードバック制御のポイントは、出力と目標値を比較したうえで制御量を決めることです。
つまり、出力と目標値を比較するために、出力信号が入力側に戻らなければなりません。
ブロック線図で示される、一般的なフィードバック制御を図3に示します。
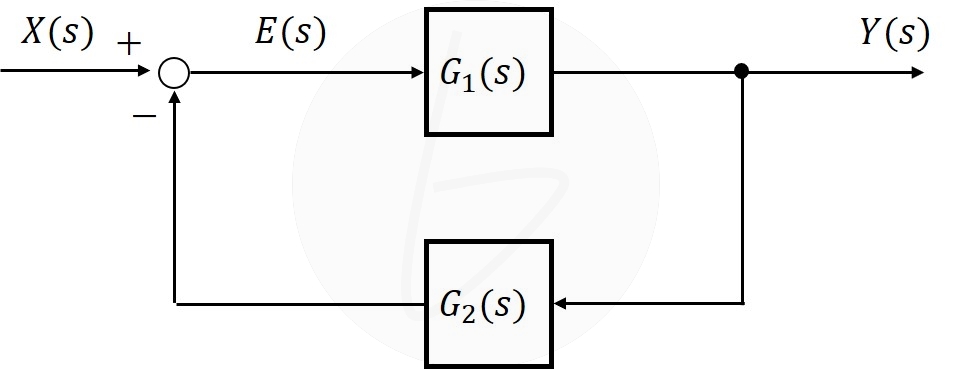
図3 フィードバック制御系のブロック線図
図3をフィードバック制御系の目的に沿って補足を加えると、図4になります。
図4では、出力$Y\left(s\right)$が入力側に戻され(フィードバックされ)、目標値との差$E\left(s\right)$が計算されています。
一般化のために、$Y\left(s\right)$のフィードバック経路に要素$G_2\left(s\right)$を配置していますが、$G_2\left(s\right)=1$と考えれば、システムの入力は$X\left(s\right)-Y\left(s\right)$となるのでイメージしやすいでしょう。
これによって、システムの偏差$E\left(s\right)=0$、すなわち出力$Y\left(s\right)={\rm 目標値}X\left(s\right)$となるような制御が行われることになります。

図4 一般的なフィードバック制御のブロック図
フィードバック制御系の伝達関数の公式の導出
フィードバック系の伝達関数の公式を導出していきます。
この公式は、自動制御では頻出なので、すぐに使えるようにしておくといいです。
再掲にはなりますが、図5に、フィードバック制御系の基本構成を示します。

図5 フィードバック制御系の伝達関数
図5の伝達関数において、
$$\begin{cases}
Y\left(s\right)=G_1\left(s\right)E\left(s\right)\\
E\left(s\right)=X\left(s\right)-G_2\left(s\right)Y\left(s\right)
\end{cases}\tag{1}$$
となります。
以上より、
$$Y\left(s\right)=G_1\left(s\right)\left(X\left(s\right)-G_2\left(s\right)Y\left(s\right)\right)\tag{2}$$
$$\left(1+G_1\left(s\right)G_2\left(s\right)\right)Y\left(s\right)=G_1\left(s\right)X\left(s\right)\tag{3}$$
最終的に、フィードバック制御系の伝達関数$G\left(s\right)$は、
$$G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{G_1\left(s\right)}{1+G_1\left(s\right)G_2\left(s\right)}\tag{4}$$
となります。
ここで、
- $G_1\left(s\right)$:前向き伝達関数
- $G_1\left(s\right)G_2\left(s\right)$:一巡伝達関数
と呼びます。
前向き伝達関数、一巡伝達関数について図示すると、図6のようになります。
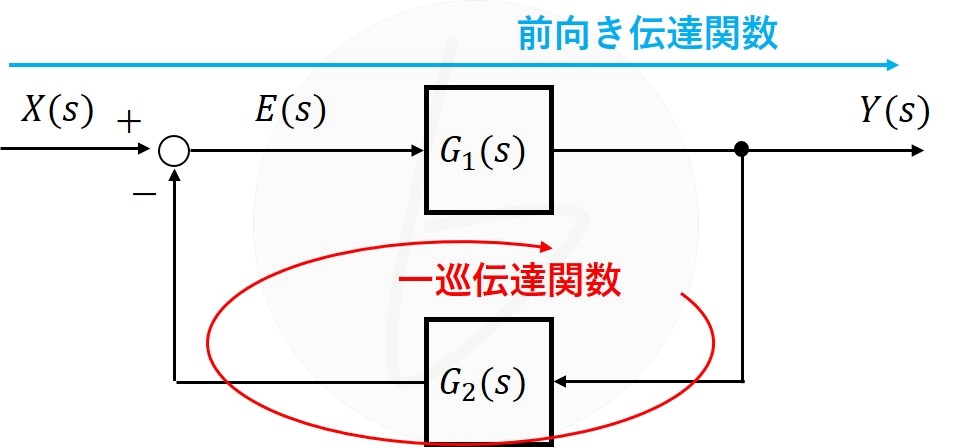
図6 前向き伝達関数と一巡伝達関数
最終的に、フィードバック制御系の伝達関数の公式として、
$$G\left(s\right)=\frac{{\rm 前向き伝達関数}}{1+{\rm 一巡伝達関数}}\tag{5}$$
となります。
フィードバック制御系は、自動制御の基本形であるため、上記の公式は多用します。
もちろん、ブロック線図を追っていけばすぐに求めることができる公式ではありますが、回答するときの時間短縮になります。
電気主任技術者試験に限らず、一般的な話として、式(5)の公式は、既知のものとして使用して問題ないです。
回答時間の短縮になるので、ブロック線図の簡単化などと含めて、使いどころを見極めた上で活用していくと便利です。
まとめ
ここまで、
- フィードバック制御の目的
- フィードバック制御系の伝達積関数の計算公式
について説明してきました。
フィードバック制御は、目標値と出力の差を0にすることが目的です。
フィードバック制御は湯沸かしや車の運転、他の家電(エアコンとかもそう)で、身近に行われています。
そして、湯温や速度、部屋の温度が目標値に一致するから、快適な生活を行えるようになっているわけです。
フィードバック制御系の目的が理解できれば、計算公式として、
$$G\left(s\right)=\frac{{\rm 前向き伝達関数}}{1+{\rm 一巡伝達関数}}$$
を覚えておけば問題ないでしょう。
なお、フィードバック制御は、偏差を0にすることを目的にする制御ですが、必ずしも偏差が0になるとは限りません。
無限に長い時間が経過しても残る偏差を定常偏差といいます。
フィードバック制御の例と合わせて、フィードバック制御系の定常偏差と定常偏差を0にする方法についても確認しておいてください。
以上、フィードバック制御の身近な例と、伝達関数の公式の導出について、参考になれば幸いです。
●紙の本:3,850円(税込)
電験2種 二次試験 機械・制御で出題される自動制御を完答することを目的に作成した参考書。
機械・制御において、自動制御で満点を狙い、確実に合格したい場合には、この参考書がおすすめです。




