みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
この記事では、平成30年度 電験2種 2次試験 電力・管理 問5の過去問解説をします。
高調波に関する問題で、基本的な内容が確認できる問題になっています。
第$n$次高調波に対して、
- インダクタは$jnX_L$
- コンデンサは$\frac{1}{n}X_C$
とすることを知っていれば、分流の計算で求めることができます。
平成30年度 電験2種 2次試験 電力・管理 問5 問題文
図は系統電源に接続された自家用電気設備の単線結線図である。変圧器の2次側母線には高調波を発生する負荷設備と力率改善用の直列リアクトル付進相コンデンサ設備が設置されている。$X_T$, $X_L$, $X_C$は、それぞれ変圧器、直列リアクトル、進相コンデンサの基本波におけるリアクタンスの大きさ(${\rm Ω}$値)である。また、電流$I_H$, $I_S$, $I_C$は、それぞれ高調波発生負荷からの高調波電流、系統電源側に流出する高調波電流、進相コンデンサ設備に流入する高調波電流とする。このとき、次の問に答えよ。ただし、系統電源側のインピーダンス及び変圧器の抵抗分は無視するものとする。
(1)$n$次高調波電流源を電源とする高調波等価回路を描くとともに、$I_{Hn}$, $I_{Sn}$, $I_{Cn}$それぞれに対し、電流の方向を矢印で示せ。ただし、$n$次高調波電流源の電流を$I_{Hn}$、系統電源側に流出する$n$次高調波電流を$I_{Sn}$、進相コンデンサ設備に流入するn次高調波電流を$I_{Cn}$とする。
(2)(1)の$n$次高調波等価回路において、$n$次高調波電流源の電流$I_{Hn}$と各部のリアクタンスの大きさを用いて、進相コンデンサ設備に流入する$n$次高調波電流$I_{Cn}$を表す式を示せ。
(3)$I_{Cn}$を表す式において、回路で共振を起こす条件式を示せ。
(4)$I_{Cn}$を表す式において、進相コンデンサ設備に流入する$n$次高調波電流が、高調波発生源の電流よりも大きくならないようにするための条件を示せ。
$n=5$(第5高調波)の場合、直列リアクトルのリアクタンスの大きさは進相コンデンサのリアクタンスの大きさの何$\left[\%\right]$以上であることが必要か示せ。
(5)$6\%$直列リアクトル付進相コンデンサ設備の場合、高調波発生源に第3高調波が多く含まれていた場合、進相コンデンサの容量によっては共振状態となり、第3高調波電流が異常に増大する場合がある。このとき、進相コンデンサのリアクタンスの大きさ$X_C\left[{\rm Ω}\right]$と変圧器のリアクタンスの大きさ$X_T\left[{\rm Ω}\right]$の関係式を示せ。また、進相コンデンサ容量は変圧器容量の何$\left[\%\right]$か示せ。変圧器の容量を$P_T\left[{\rm kV・A}\right]$、変圧器のパーセントリアクタンス$\%X_T$を$7.5\%$(自己容量基準)、進相コンデンサ容量を$Q_C\left[{\rm kvar}\right]$として計算せよ。
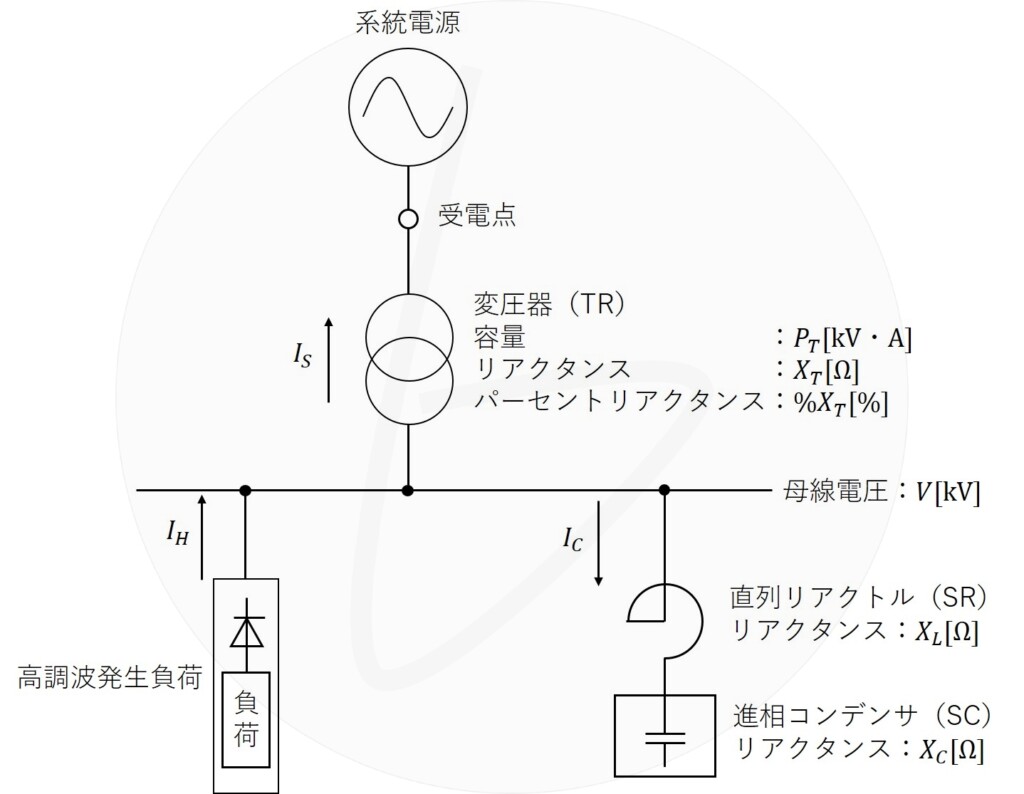
図 自家用電気設備と高調波電流
解答・解説
小問(1)第n次高調波に対する等価回路の導出
高調波の等価回路を考える際、基本周波数の電圧源は短絡、電流源は解放し、インダクタンスを$n$倍、キャパシタンスを$\frac{1}{n}$倍する。
以上より、解図1の通りになる。

解図1
解図1を整理すると、解図2の通りになる。

解図2
(答)解図2に示す通り。
小問(2)進相コンデンサに流入する第n次高調波電流の計算
解図2より、並列回路において電流$I_{Hn}$はインピーダンスの逆比で分流するので、
$$\begin{align}
I_{Cn}&=\frac{jnX_T}{jnX_T+\left(jnX_L-j\frac{X_C}{n}\right)}I_{Hn}\\
&=\frac{nX_T}{nX_T+\left(nX_L-\frac{X_C}{n}\right)}I_{Hn}\tag{1}
\end{align}$$
となる。
(答)$I_{Cn}=\frac{nX_T}{nX_T+\left(nX_L-\frac{X_C}{n}\right)}I_{Hn}$
小問(3)第n次高調波電流の共振条件
共振する条件は、式(1)において、分母=0なので、
$$nX_T+\left(nX_L-\frac{X_C}{n}\right)=0\tag{2}$$
(答)$nX_T+\left(nX_L-\frac{X_C}{n}\right)=0$
小問(4)直列リアクトルのリアクタンス計算
$n$次高調波電流が、高調波発生源の電流よりも大きくならない条件は、
$$\begin{align}
I_{Cn}&=\frac{nX_T}{nX_T+\left(nX_L-\frac{X_C}{n}\right)}I_{Hn}\\
&≦I_{Hn}\tag{3}
\end{align}$$
である。
整理すると、
$$nX_L-\frac{X_C}{n}≧0\tag{4}$$
となる。
第5高調波の場合、$n=5$であるから、
$$5X_L-\frac{X_C}{5}≧0\tag{5}$$
$$XL≧\frac{1}{5^2}X_C=0.04X_C\tag{6}$$
(答)高調波発生源の電流よりも大きくならない条件:$nX_L-\frac{X_C}{n}≧0$、第5高調波に必要となる直列リアクトルの大きさ:$4.00\%$以上
小問(5)第3高調波電流の共振条件
直列リアクトルが$6\%$の時、
$$X_L=0.06X_C\tag{7}$$
であり、式(1)に第3高調波なので$n=3$及び式(7)を代入すると、高調波電流は、
$$I_{Cn}=\frac{3X_T}{3X_T+\left(3×0.06X_C-\frac{X_C}{3}\right)}I_{Hn}\tag{8}$$
となる。
共振状態の時、分母=0なので、
$$3X_T+\left(3×0.06X_C-\frac{X_C}{3}\right)=0\tag{9}$$
$$X_C=\frac{9}{0.46}X_T\tag{10}$$
となる。
次に、変圧器容量$X_T\left[{\rm kV・A}\right]$と、進相コンデンサ容量$Q_C\left[{\rm kV・A}\right]$の比率を求める。
まず変圧器リアクタンス$X_T\left[{\rm Ω}\right]$について、
$$\begin{cases}
{\rm 基準容量:}&P_T\left[{\rm kV・A}\right]\\
{\rm 基準電圧:}&V\left[{\rm kV}\right]\\
{\rm 基準電流:}&I_{BASE}=\frac{P_T}{3×\frac{V}{\sqrt{3}}}=\frac{P_T}{\sqrt{3}V}\left[{\rm A}\right]\\
{\rm 基準インピーダンス:}&Z_{BASE}=\frac{\frac{V}{\sqrt{3}}×10^3}{\frac{P_T}{\sqrt{3}V}}=\frac{V^2×10^3}{P_T}\left[{\rm Ω}\right]
\end{cases}\tag{11}$$
であるので、
$$\%X_T=\frac{X_T}{Z_{BASE}}×100\tag{12}$$
$$\begin{align}
X_T&=\frac{\%X_T}{Z_{BASE}}100\\
&=\frac{\%X_T}{100}・\frac{V^2×10^3}{P_T}\\
&=\frac{\%X_TV^2}{P_T}×10\tag{13}
\end{align}$$
これより、進相コンデンサのリアクタンス$X_C\left[{\rm Ω}\right]$は、式(10)より
$$X_C=\frac{9}{0.46}\frac{\%X_TV^2}{P_T}×10\tag{14}$$
となる。
進相コンデンサに、電圧$\frac{V}{\sqrt{3}}\left[{\rm kV}\right]$を印加したときに流れる電流$I_C$は、
$$\begin{align}
I_C&=\frac{\frac{V}{\sqrt{3}}×10^3}{X_C}\\
&=\frac{\frac{V}{\sqrt{3}}×10^3}{\frac{9}{0.46}\frac{\%X_TV^2}{P_T}×10}\\
&=\frac{0.46P_T×10^2}{9\sqrt{3}・\%X_TV}\tag{15}
\end{align}$$
となる。
進相コンデンサの容量$Q_C\left[{\rm kV・A}\right]$は、
$$\begin{align}
Q_C&=\frac{3\frac{V×10^3}{\sqrt{3}}I_C}{1000}\\
&=3\frac{V}{\sqrt{3}}\frac{0.46P_T×10^2}{9\sqrt{3}・\%X_TV}\\
&=3\frac{V}{\sqrt{3}}×\frac{0.46P_T×10^2}{9\sqrt{3}・7.5×V}\\
&=0.68152146406P_T\tag{16}
\end{align}$$
よって、$68.2\left[\%\right]$となる。
(答)$X_C=\frac{9}{0.46}X_T$, $68.2\left[\%\right]$
本問は、問題設定として、コンデンサの容量Q_Cが何を基準にする容量なのかあいまいです。
結果的には、母線電圧V[kV]基準の進相コンデンサ容量を求める問題でしたが、もしも進相コンデンサとして運転中の容量となれば、直列リアクトルの電圧降下を考える必要があり、結果が変わります。
問題文の状況設定が説明不足な感じで、「母線電圧$V\left[{\rm kV}\right]$基準の進相コンデンサ容量$Q_C\left[{\rm kV・A}\right]$を求めよ」としている方が、親切に思います。
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






