みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、制御理論の基礎となる、伝達関数とブロック線図です。
古典制御を学ぶ上で、制御システムをブロック線図で表し、信号の流れを読み取ることは重要です。
現代制御理論にもつながってくる部分なので、確実に理解しておきましょう。
ブロック線図の等価変更の重要事項
ブロック線図は
- ブロック
- 引出し点
- 加え合わせ点
で構成され、等価変換によって簡単な表現に書き変えることができる。
 |
 |
| 加え合わせ点を要素の後に移動 | |
 |
 |
| 加え合わせ点を要素の前に移動 | |
 |
 |
| 引出し点を要素の後に移動 | |
 |
 |
| 引出し点を要素の後に移動 | |
復習:ブロック線図の基本
伝達関数は、様々な基本関数や微分・積分で示される入出力関係を、ラプラス変換によって四則演算に変換し、比率として示したものです。
また、伝達関数はブロック線図として信号の流れを図示できます。
以前、伝達関数とブロック線図については基本事項を説明しましたが、ここでもう一度復習しておきましょう。
掛け算・割り算を表現する「ブロック」
入力信号$x\left(t\right)$、出力信号$y\left(t\right)$をラプラス変換したものをそれぞれ$X\left(s\right)$、$Y\left(s\right)$、その伝達関数を$G\left(s\right)$とすれば、入力$X\left(s\right)$を伝達関数$G\left(s\right)$倍すれば出力$Y\left(s\right)$となるため、
$$Y\left(s\right)=G\left(s\right)X\left(s\right) \tag{1}$$
となります。
この掛け算(あるいは割り算)を表現するものがブロックであり、図1に示すような表現ができるようになります。
ブロックに入力された信号$X\left(s\right)$は、ブロックを通過すると、そのブロックの伝達関数$G\left(s\right)$され、出力$Y\left(s\right)$とまります。
まさに、式(1)そのものを表していることになります。
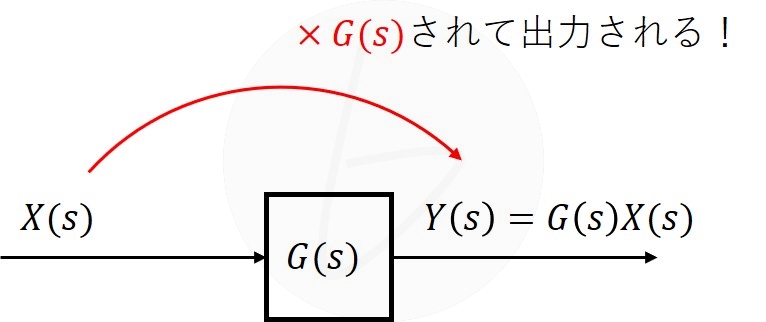
図2 掛け算を表現するブロック線図
なお、図3に示す通り、逆数にすれば割り算も表現できます。
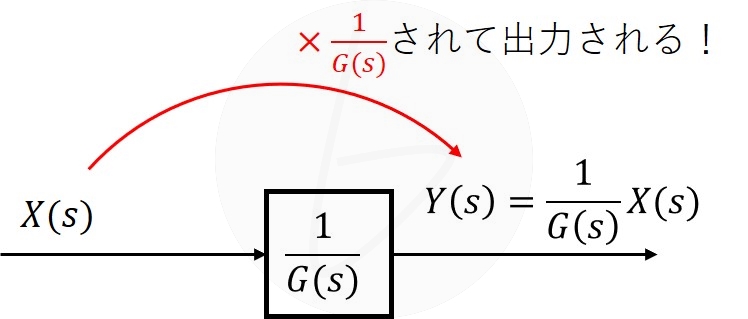
図3 割り算を表現するブロック線図
以上のように、ブロック線図のブロックは掛け算や割り算を示しており、ブロックに入った信号波、$G(s)$倍されて出力されます。
足し算・引き算を表現する「加え合わせ点」と「引出し点」
ブロック線図には、図4に示すような「加え合わせ点」があり、足し算、引き算も表現できます。
引出し点では、信号が分岐します。信号が分岐して、並列に流れ、最終的に加え合わせ点で合流するような表現が多用されます。
.jpg) (a)加え合わせ点(加算の場合) |
.jpg) (b)加え合わせ点(減算の場合) |
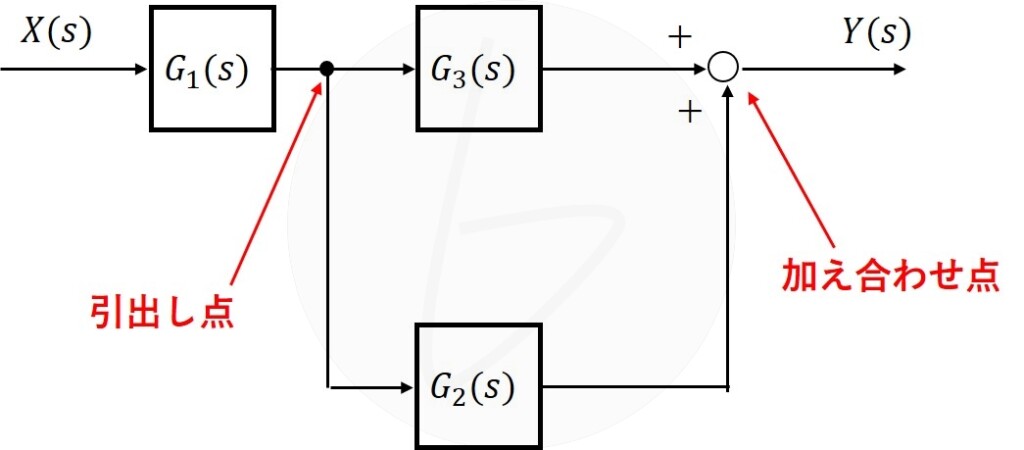 (c)引出し点(信号分岐) |
|
図4 伝達関数の加え合わせ点
ブロック線図の等価変換
ブロック線図は、一見ややこしい構造であっても、等価変換により簡単化することができます。
等価変換については基本となる4パターンを紹介します。
加え合わせ点を要素の後に移動する
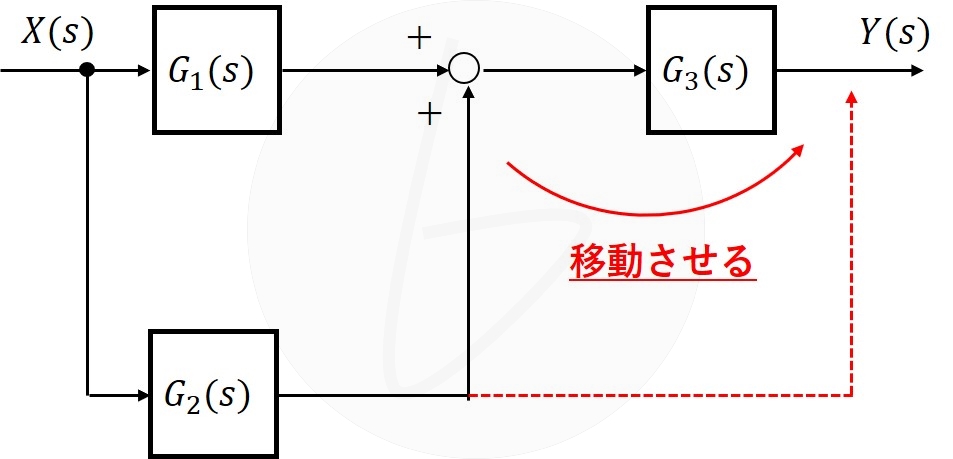
加え合わせ点を$G_3\left(s\right)$の後ろに移動させることを考えます。
図5の赤の点線のように変換したい場合、加え合わせる前に$G_3\left(s\right)$を掛け算すれば、同じ結果を得られます。
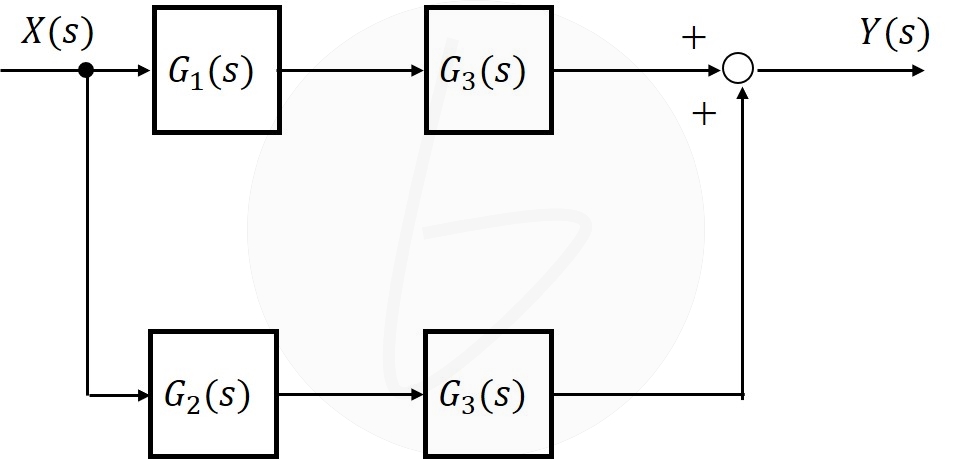
等価変換の結果、図6のようになります。

図5 加え合わせ点を要素の後への移動(移動前)

図6 加え合わせ点を要素の後への移動(移動後)
加え合わせ点を要素の前に移動する
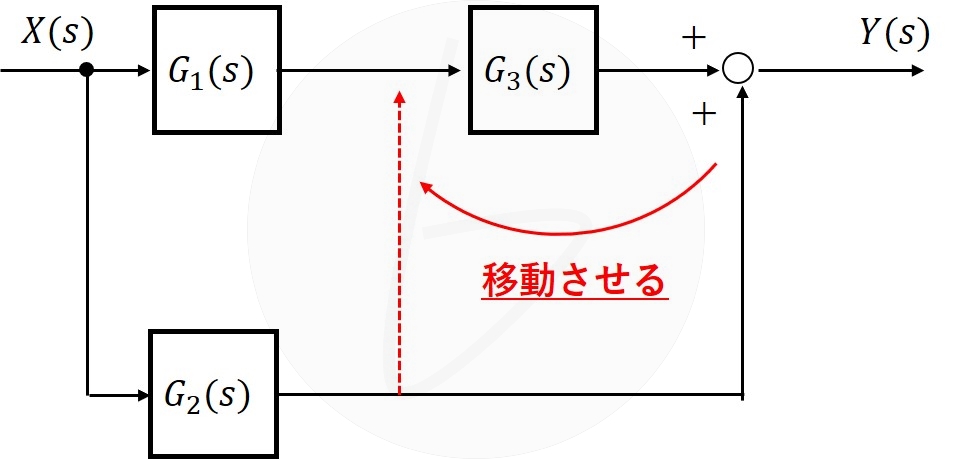
加え合わせ点を、$G_3\left(s\right)$の前に移動させる場合を考えます。
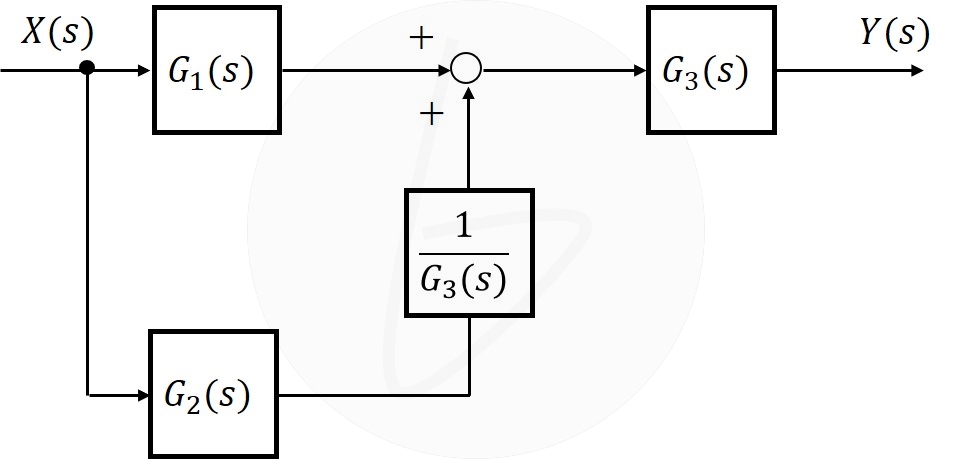
図7の赤の点線のように変換したい場合、加え合わせる前に$\frac{1}{G_3\left(s\right)}$を掛け算すれば、同じ結果を得られます。等価変換の結果、図8のようになります。

図7 加え合わせ点を要素の前への移動(移動前)

図8 加え合わせ点を要素の前への移動(移動後)
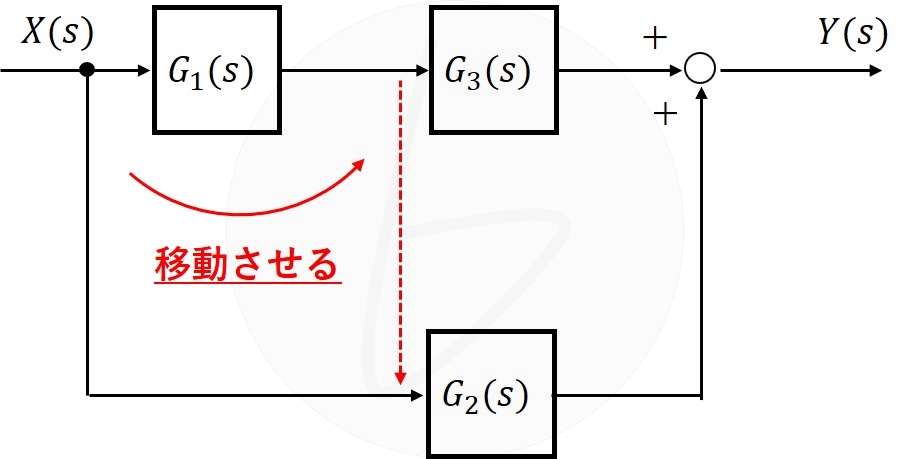
引出し点を要素の後に移動する
引出し点を、$G_1\left(s\right)$の後に移動させる場合を考えます。
図9の赤の点線のように変換したい場合、引き出した後に$\frac{1}{G_1\left(s\right)}$を掛け算すれば、同じ結果を得られます。
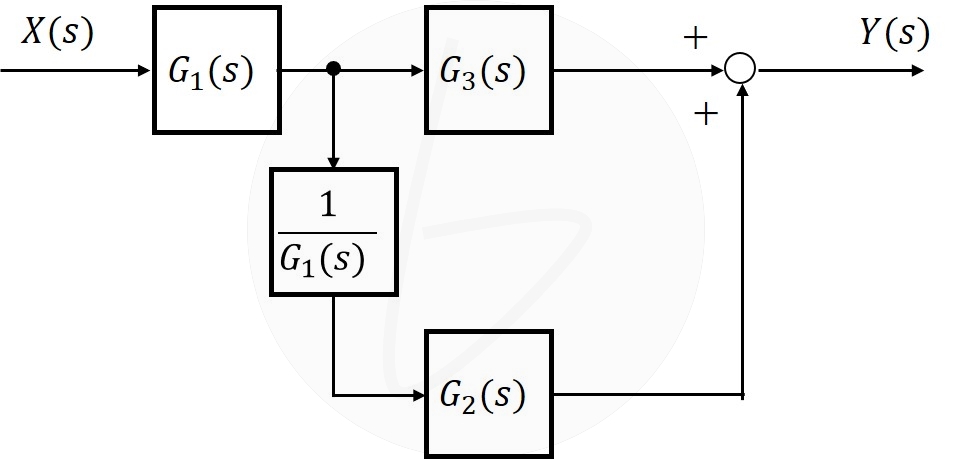
等価変換の結果、図10のようになります。

図9 引出し点を要素の後に移動(移動前)

図10 引出し点を要素の後に移動(移動後)
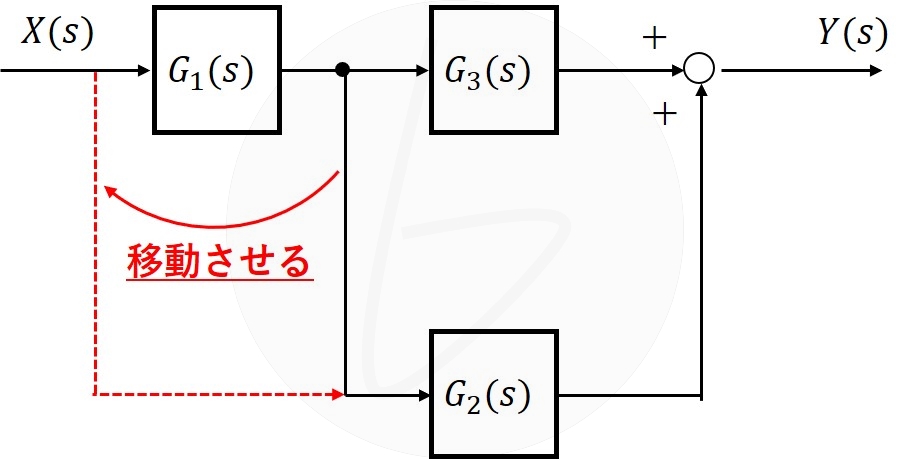
引出し点を要素の前に移動する
引出し点を、$G_1\left(s\right)$の前に移動させる場合を考えます。
図11の赤の点線のように変換したい場合、加え合わせる前に$G_1\left(s\right)$を掛け算すれば、同じ結果を得られます。
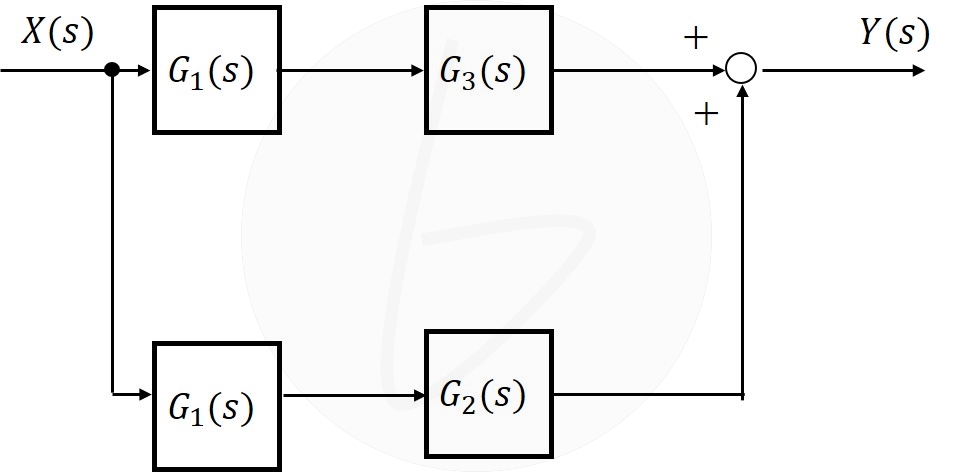
等価変換の結果、図12のようになります。

図11 引出し点を要素の前に移動(移動前)

図12 引出し点を要素の前に移動(移動後)
まとめ
ここまで、ブロック線図の等価変換について説明してきました。
ブロック線図は制御系の信号の流れを理解するのに重要ですし、等価変換も、より簡単なブロック線図に書き変えるために使用したりします。
また、現代制御理論でも、状態方程式の導出において、ブロック線図の等価変換に近いイメージを使います。
確実に理解しておきましょう。
伝達関数について再度確認したい方は、伝達関数とブロック線図の基本について解説した記事があるので、参考にしてください。
その他、制御の本質であるフィードバック制御系について、
- 身近なフィードバック制御の例
- フィードバック制御系の伝達関数の公式
を解説した、フィードバック制御系の解説記事もよく読まれています。
●紙の本:3,850円(税込)
電験2種 二次試験 機械・制御で出題される自動制御を完答することを目的に作成した参考書。
機械・制御において、自動制御で満点を狙い、確実に合格したい場合には、この参考書がおすすめです。





