この記事では、令和4年度 電験2種 二次試験 電力・管理 問1の過去問解説をしています。
調整池式の水力発電所の計算問題で、自然流量と貯水によって発電できる、、ピーク負荷とオフピーク負荷の発電量を計算する問題です。
若干問題設定がややこしいですが、確実に得点源になる問題なので、正確に題意をつかみましょう。
令和4年度 電験2種 二次試験 電力・管理 問1
調整池式の水力発電所の運用に関して、次の問に答えよ。
有効貯水量$180×{10}^3{\rm m^3}$の調整池を有する有効落差$60{\rm m}$の水力発電所がある。自然流量が$20{\rm m^3/s}$であるとき、図に示す負荷曲線で運転した場合のピーク負荷時の出力$\left[{\rm kW}\right]$及びオフピーク負荷時の出力$\left[{\rm kW}\right]$を求めよ。ただし、年間を通して毎日同様の運転を繰り返すものとし、調整池は最大限活用し、オフピーク負荷時には越流させないこととする。
なお、水車と発電機の合成効率は、ピーク負荷時出力で$85\%$、オフピーク負荷時出力で$80\%$とする。
また、発電機の定格出力はピーク負荷を十分供給できるものとする。
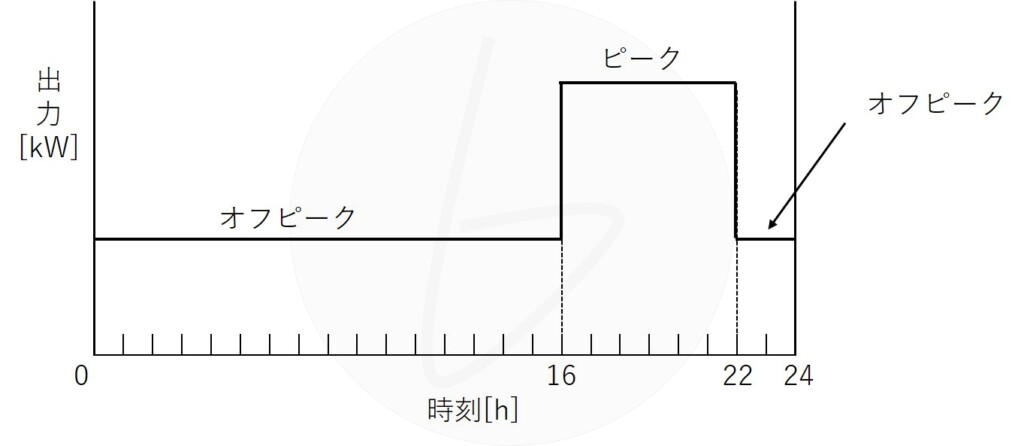
図 負荷曲線(運転パターン)
解答・解説
この問題の問題設定ですが、文章だけでは少しわかりにくいので確認しておきます。
問題設定としては、主に水車発電機に流入する水の流量を計算する問題となります。
ピーク負荷時には自然流量$20\left[{\rm m^3/s}\right]$に加え、貯水池$180×{10}^3\left[{\rm m^3}\right]$の水を6時間で放水します。
つまり、発電に使われるのは自然流量+放水量となります。
一方オフピーク負荷時には自然流量$20\left[{\rm m^3/s}\right]$の自然流量から、18時間で貯水池に水をためるための水を按分します。つまり、発電に使われるのは自然流量-貯水量となります。
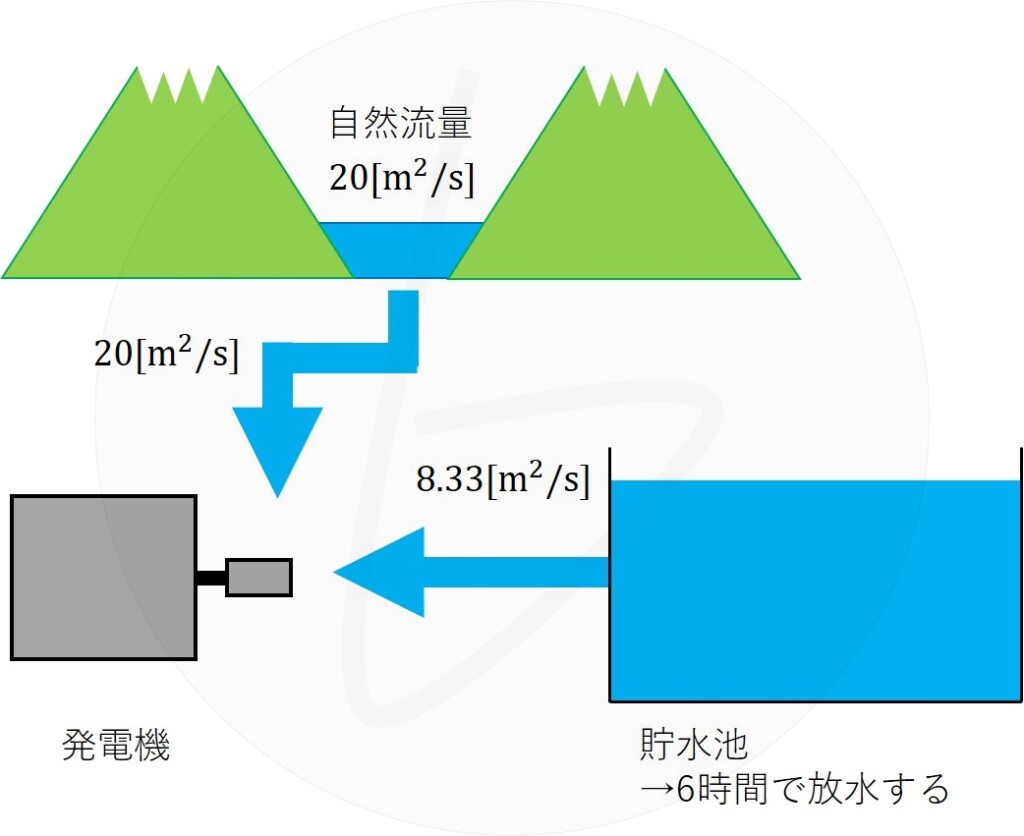
(a)ピーク時(自然流量+放水量)
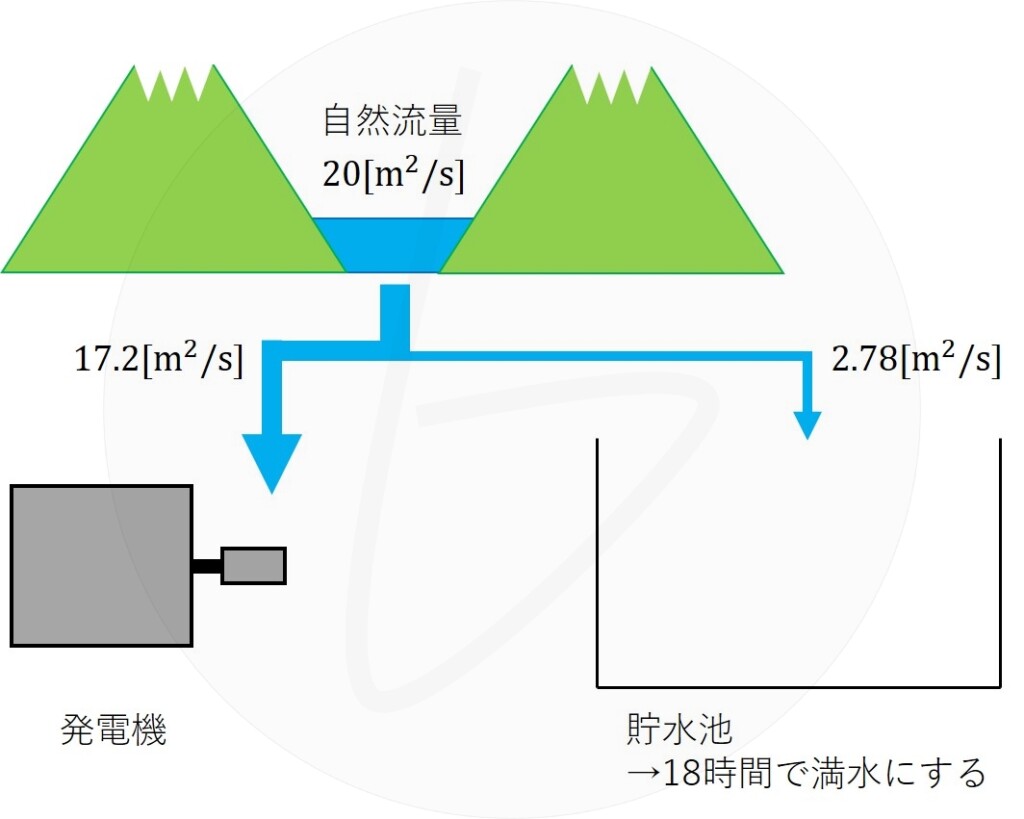
(b)オフピーク時(自然流量-貯水量)
ピーク時の流量計算
ピーク時には、16時の時点で貯水池が満水になっており、それらの水を22時までの6時間で放出する。
この時の流量は、
$$\frac{180×10^3}{6×3600}=8.33333333333\left[{\rm m^3/s}\right]\tag{1}$$
となる。
式(1)で計算した貯水池からの流量に、自然流量$20\left[{\rm m^3/s}\right]$が加わるので、ピーク時に発電に使用される流量$Q_{peak}$は、
$$Q_{peak}=28.3333333333\left[{\rm m^3/s}\right]\tag{2}$$
となる。
したがって、ピーク時の発電量$P_{peak}$は、流量$Q_{peak}$、効率$85\left[\%\right]$であるので、
$$\begin{align}
P_{peak}&=0.85×9.8×1000×28.3333333333×60\\
&=14160999.9999\left[{\rm W}\right]\\
&=14161×10^3\left[{\rm W}\right]\\
&=1.42×10^4\left[{\rm kW}\right]\tag{3}
\end{align}$$
となる。
オフピーク時の流量計算
オフピークの時は、22時から翌日16時までの間に、貯水池を満水にする必要がある。この時に必要な流量は、
$$\frac{180×10^3}{18×3600}=2.77777777777\left[{\rm m^3/s}\right]\tag{4}$$
となる。自然流量$20\left[{\rm m^3/s}\right]$から式(4)で計算した値の差分が発電に使用されるので、オフピーク負荷時に発電に使用される水の流量$Q_{off}$は、
$$\begin{align}
Q_{off}&=20-Q_s\\
&=17.2222222223\left[{\rm m^3/s}\right]\tag{5}
\end{align}$$
となる。
以上より、オフピーク時の発電量$P_{off}$は、流量$Q_{off}$、効率$80\left[\%\right]$であるので、
$$\begin{align}
P_{off}&=0.8×9.8×1000×17.2222222223×60\\
&=8101333.33332\left[{\rm W}\right]\\
&=8101×10^3\left[{\rm W}\right]\\
&=8.10×10^3\left[{\rm kW}\right]\tag{6}
\end{align}$$
となる。
(答)ピーク負荷時の出力:$1.42×{10}^4\left[{\rm kW}\right]$、オフピーク負荷時の出力:$8.10×{10}^3\left[{\rm kW}\right]$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






