令和元年度電験2種電力・管理問3 電力系統の過渡安定性の論説

電力系統の過渡安定性に関して、次の問に答えよ。

（1）図1の1機無限大母線系統の過渡安定性について考える。発電機は、過渡リアクタンスを無視し、電圧$E_1\angle\delta$で表され、送電線路は、1回線あたりのリアクタンスが$X_t$の送電線が2回線併用されているものとする。また、発電機の機械的入力を$P_m$、無限大母線の電圧を$E_0\angle0$とする。
送電端の至近で1回線三相地絡事故が発生し、同回線の両端の遮断器を開放することで事故を除去した場合を想定したとき、事故発生前、事故継続中、事故除去後の電力相差角曲線（$P-\delta$曲線）は図2の通り表される。ここに、事故が除去された時の$\delta$を$\delta_a$とし、$\delta$はその後、$\delta_b$まで至ったものとするとき、図2の面積abcdと面積defgのそれぞれについて、発電機の加速エネルギー又は減速エネルギーのどちらを表すかを答えよ。

（2）事故除去が遅れ、$\delta_a$が大きくなった場合、過渡安定性を維持できる限界について、図2に示されている記号を用いて簡潔に説明せよ。

（3）図1の送電線路の中間点に開閉所を設置した図3の系統において、小問（1）と同じ事故が発生し、事故が発生した回線の両端の遮断器を開放することで事故を除去した場合を想定する。このとき、事故除去後の電力相差角曲線の電力の最大値は、開閉所の設置前の何倍になるかを答えよ。

（4）小問（3）の開閉所の設置により、過渡安定性が向上するか低下するかについて、加速エネルギーと減速エネルギーの変化に触れながら200字程度以内で説明せよ。

（5）図3の系統において、送電線路の中間点に当たる開閉所に無効電力を高速に補償する装置を設置し、事故除去後、位相角$\delta$が最大値に至るまでの間、遅れ無効電力を系統側に注入した場合、小問（3）のときと比べ、位相角$\delta$の最大値はどう変化するか。加速エネルギーと減速エネルギーの変化に触れながら200字程度以内で述べよ。

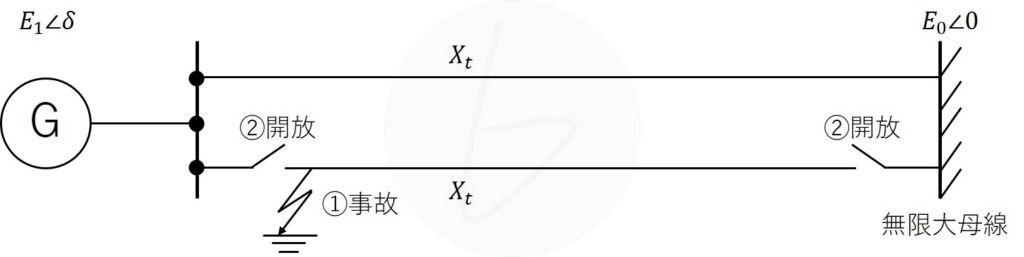
図1

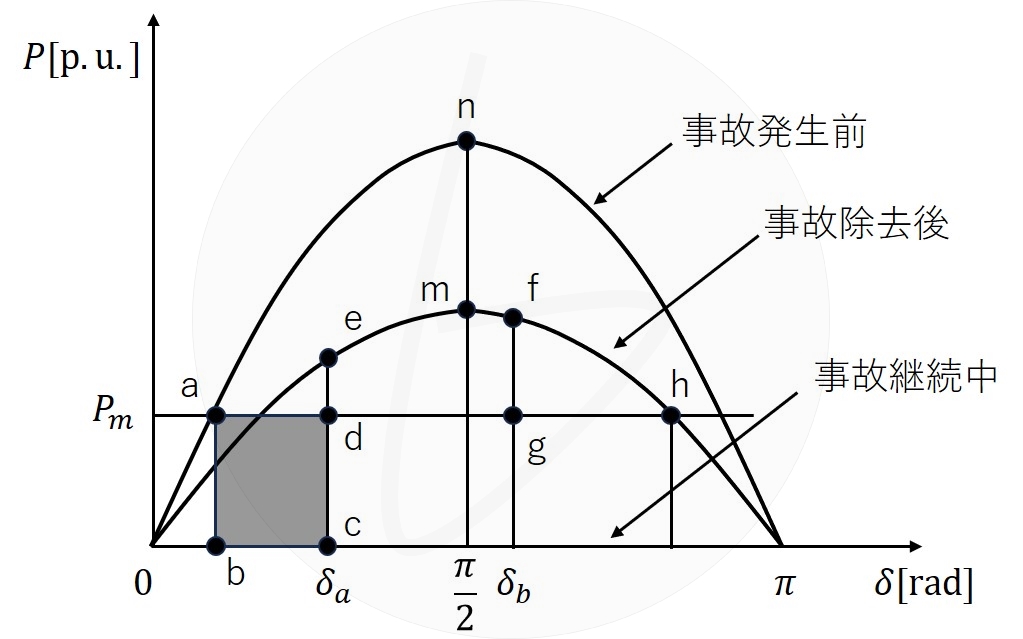
図2

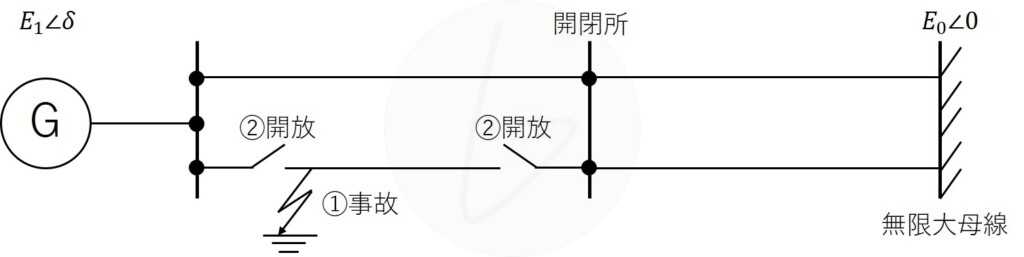
図3

試験センター標準解答

※解説は、小問（1）～（5）をまとめて行います。

小問（1）：発電機の加速エネルギーと減速エネルギー

面積abcd：加速エネルギー，面積defg：減速エネルギー

小問（2）：過渡安定性を維持できる限界

面積abcdと面積dehが等しくなる場合が過渡安定性を維持できる限界となる。

小問（3）：事故除去後の電力の最大値

電力相差角曲線の電力の最大値は，電源と無限大母線の間のリアクタンスに反比例する。開閉所設置前の事故除去後のリアクタンスは$X_t$ ，開閉所設置後の事故除去後のリアクタンスは$\frac{X_t}{2}+\frac{X_t}{2}÷2=\frac{3X_t}{4}$であるから，電力相差角曲線の電力の最大値は$\frac{4}{3}$倍となる。

（4）：過渡安定度の変化

加速エネルギーは開閉所設置前と変わらないが，事故除去後に位相角がある値に至るまでの減速エネルギーは開閉所設置前より増加することから，過渡安定性が向上する。

（5）：無効電力の高速補償と安定性

遅れの無効電力を系統側に注入することで，系統の電圧が上昇することから，事故除去後の電力相差角曲線がP軸の正方向に大きくなる。加速エネルギーは変わらないが，事故除去後に位相角がある値に至るまでの減速エネルギーは小問(3)のときより増加することから，位相角$\delta$の最大値は小さくなる。

電力系統の過渡安定度

送出電力と動揺方程式

同期発電機の送電電力$P_e$は、発電機端子電圧$E_0$、受電端電圧$E_1$、相差角$\delta$、送電線のリアクタンス$X$とすれば、

$$P_e=3\frac{E_0E_1}{X}sin\delta\tag{1}$$

で示されます。

また、動揺方程式は、発電機の角速度$\omega$、機械的入力$P_m$として、

$$M\frac{d\omega}{dt}=P_m-P_e\tag{2}$$

で示されます。

発電機の動揺

ここで機械的入力（タービンに流入する水蒸気のエネルギーなど）は常に一定値と仮定しましょう。

この場合、動揺方程式から、事故が生じた際に発電機の挙動は以下の3パターンになります。

(a)P_m=P_e：発電機回転数と系統周波数の一致（相差角は増加しない。）

(b)P_m>P_e：発電機が加速（余剰のP_m-P_eが発電機の運動エネルギーに変換される。）

(c)P_m<P_e：発電機減速（不足エネルギーP_e-P_mを発電機運動エネルギーから奪う。）

解図1　動揺方程式の意味

等面積法

以上の挙動を基にすれば、解図2の通り理解できます。

a→b	事故が発生し、送電電力$P_e$が瞬時に$0$になりb点に移動します。
b→c	事故が継続中、常に$P_e=0$が継続するので、解図1(b)の状況になり、再閉路するまで相差角が増大し続けます。この時、$P_m-P_e$、つまり、abcdで囲まれた面積のエネルギーで発電機は加速します。
c→e	再閉路されると、その時の相差角$\delta$に対応した電力を送電します。送電電力は$sin\delta$で決まり、また事故継続中に$\delta$は増大しているので、この時の送電電力はa点の送電電力より大きく、$P_m<P_e$となり、ちょうど解図1(c)に対応します。つまり発電機は徐々に減速し始めます。
e→f	発電機は徐々に減速し続け、やがて系統周波数と同じになり、相差角の増大が止まります。この時がf点に相当します。したがって、発電機は到達するとdefgで囲まれた面積のエネルギーを放出し、減速します。
f→●	f点ではまだ$P_m<P_e$の状況が継続するので発電機はさらに減速を続け、新たな平衡点である●に到達します。発電機は●近傍で軽微な加速・減速を繰り返しながら（動揺しながら）、最終的に●で一定になります。