みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、直流発電機の電圧変動率と、電圧変動率から無負荷誘導起電力を計算する方法について説明していきます。
電圧変動率や無負荷誘導起電力の概念自体は、変圧器や同期発電機の時と同じです。
直流発電機の場合、直流回路の計算であるため、電圧変動率の計算は、変圧器の電圧変動率や同期機の電圧変動率と比較して非常にシンプルです。
位相関係などの複雑な話を考えなくていいので、直感的に理解しやすいと思います。
直流発電機の電圧変動率
直流発電機が定格速度、定格定格電圧、定格電流で運転しているとき、負荷を切り離した際に生じる端子電圧の上昇分との比率について、定格電圧との比率を電圧変動率といい、
$$\epsilon=\frac{V_0-V_n}{V_n}×100\left[\%\right]$$
となる。
ただし、
- $V_0$:無負荷端子電圧
- $V_n$:定格電圧
である。
直流発電機の電圧変動率の回路動作での理解
直流発電機には電機子巻線抵抗$r_a$があり、ここに電流が流れると電圧降下が生じます。
仮に、誘導起電力として$V_0$が発生していても、定格電流$I_n$が流れていれば、電機子巻線抵抗によって$r_aI_n$の電圧降下が生じ、端子電圧$V_n$は、
$$V_n=V_0-r_aI_n\tag{1}$$
となります。
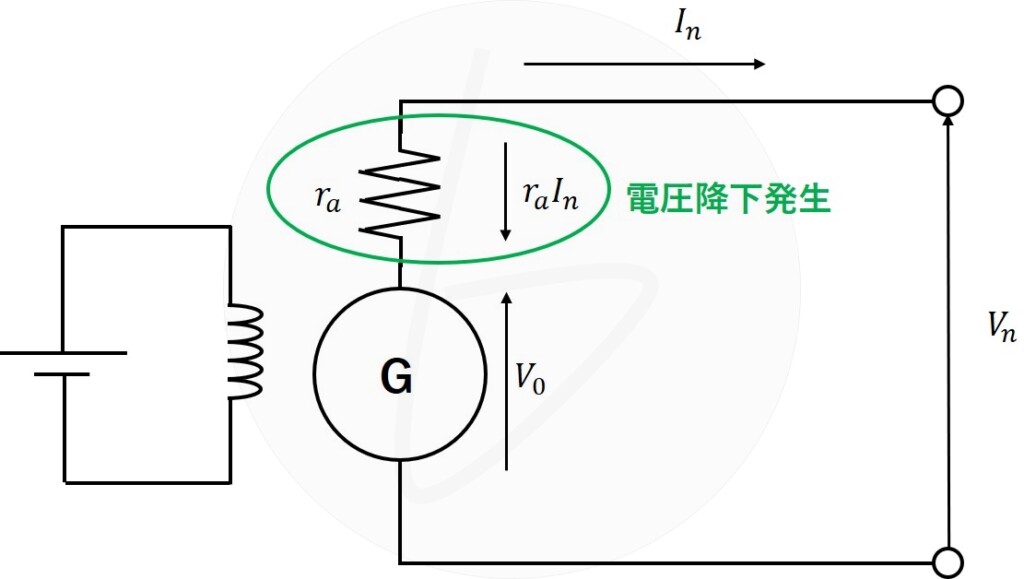
図1 負荷に電流を供給しているとき(巻線抵抗$r_a$で電圧降下が生じる)
そしてこの状況で負荷を切り離したとすれば、電流は$0\left[{\rm A}\right]$になります。
この時、電機子巻線抵抗における電圧降下も生じないため、誘導起電力$V_0$と端子電圧$V_n$は等しくなります。
つまり、負荷を切り離せば端子電圧が上昇します。

図2 負荷電流が$0\left[{\rm A}\right]$の時(巻線抵抗$r_a$で電圧降下が生じない)
この時の端子電圧の上昇量である$V_0-V_n$について、定格電圧$V_n$との比率を計算するのが電圧変動率$\epsilon$であり、
$$\epsilon=\frac{V_0-V_n}{V_n}×100\left[\%\right]\tag{2}$$
となります。
電圧変動率の分子はまさに$r_aI_n$のことであり、電圧変動率と定格電圧、定格電流が分かれば、電機子巻線抵抗$r_a$が計算できます。
このように、電圧変動率の提示によって、回路定数を計算する問題が多く出題されます。
直流発電機の電圧変動率と無負荷誘導起電力の例題
では、ここで例題を一つ挙げておきます。
問題文
図に示すような、定格電圧$V_n=200{\rm \left[V\right]}$、定格出力$P_n=2{\rm \left[kW\right]}$、電圧変動率$\epsilon=5\left[\%\right]$の直流他励発電機がある。
定格電流$I_n$、無負荷端子電圧(=無負荷誘導起電力$V_0$)及び電機子巻線抵抗$r_a$の値を求めよ。
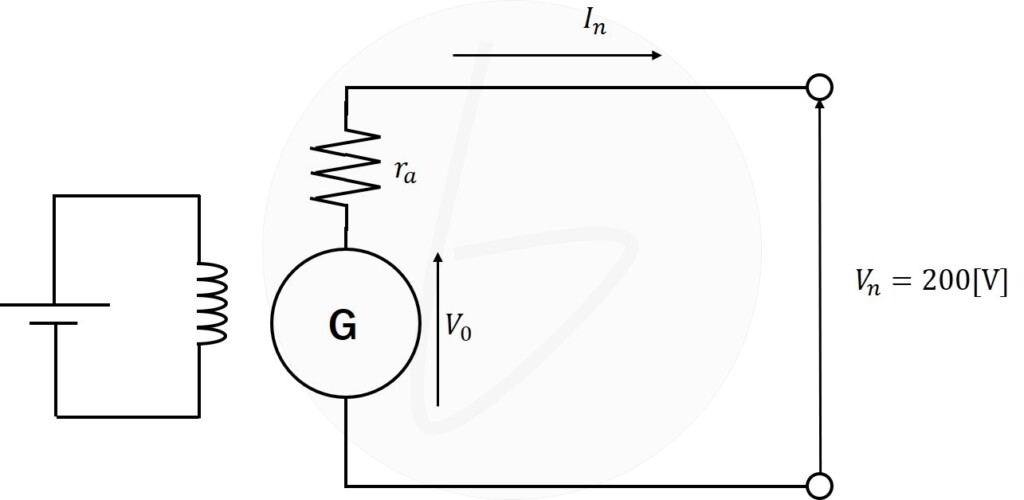
問題図
他励発電機とは、励磁電流を外部電源で運転している直流発電機です。
運転のために外部電源が必要になるので大掛かりになりますが、運転中の制御は行いやすいタイプの直流機になります。
そのため、本問においては励磁回路のことは一切考えずに解くことができます。
その他、分巻、直巻、複巻外分巻、複巻内分巻があるので、直流機の種類については以下の記事を参考にしてください。
解説
■定格電流$I_n$
まず、定格電流$I_n$を求める。
定格電圧$V_0=200{\rm \left[V\right]}$、定格出力$P_n=2{\rm \left[kW\right]}$より、定格電流$I_n$は、
$$I_n=P_nV_n=2000200=10{\rm \left[{\rm A}\right]}$$
となる。
■無負荷端子電圧(無負荷誘導起電力$V_0$)
直流発電機の無負荷端子電圧(=誘導起電力)$V_0$は、電圧変動率$\epsilon=5\left[\%\right]$、定格電圧$V_n=200{\rm \left[V\right]}$より、
$$5=\frac{V0-200}{200}×100$$
これを解いて、$V_0=210\left[{\rm V}\right]$となる。
■巻線抵抗$r_a$
ここで、求めた各値を回路図上で示すと、解図1になる。

解図1 例題における各種回路定数
解図1より、定格電流$I_n=10{\rm \left[{\rm A}\right]}$によって、$V_0-V_n=10{\rm \left[{\rm V}\right]}$の電圧降下が生じているので、電機子巻線抵抗$r_a$は、
$$r_a=\frac{V_0-V_n}{I_n}=\frac{210-200}{10}=1{\rm \left[{\rm Ω}\right]}$$
となる。
(答)$I_n=10{\rm \left[{\rm A}\right]}$、$V_0=210{\rm \left[{\rm V}\right]}$、$r_a=1.00{\rm \left[{\rm Ω}\right]}$
まとめ
ここまで、直流発電機の電圧変動率と、無負荷誘導起電力の計算方法について説明してきました。
電圧変動率の関係する問題では、直流発電機の等価回路における回路定数を計算する問題としてよく登場します。
回路定数が分かれば、直流機の並列運転時の負荷分担や、が計算できるので、併せて参考にしてください。
最近は、直流機は摩擦部(ブラシと整流子)が必要で、メンテナンスに費用が掛かるので、誘導機・同期機に置き換えられ、直流機そのもの自体がだんだん使われなくなってきています。
ただ、直流回路でありストレートに理解できるので、誘導機や同期機を理解するうえで助けになることもあります。
この記事の内容が理解できたら、変圧器の電圧変動率の計算など、ベクトル図や複素数が絡む計算にもチャレンジしてみてください。
以上、直流発電機の電圧変動率と、無負荷誘導起電力の計算方法について、参考になれば幸いです。