みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、変圧器の等価回路の紹介と、一次側換算、二次側換算について説明します。
特に電気主任技術者試験においては、変圧器の計算問題が頻繁に出題されています。
ひとまず結果だけを暗記してしまえば試験では何とかなりますが、ここでは電気回路的な原理に基づいて考えてみましょう。
なお、変圧器の等価回路は、誘導電動機の等価回路と同じものとなります。
変圧器の等価回路は、電気回路的に分断され、磁気回路として結合している1次側と2次側を、一つの電気回路で示すものです。
1次側と2次側の電圧は当然異なっているのですが、一つの回路、一つの電流の流れで示すことができる。
これは、単位法の考えが効いている部分なのですが、ここでは割愛しています。
単位法の概念としての詳細は、別途記事を作成します。
▼おすすめ記事▼

変圧器のT型等価回路とL型等価回路
比較的厳密なT型等価回路
変圧器は、コイルに交流電圧を印加し、交流電流を流します。
コイルに交流電流が流れると、右ねじの法則に従い、磁界が発生します。
※この磁界は電流が時間変化する交流なので、磁界も時間変化します。
その時間変化する磁界を鉄心を通して2次側に供給することで、2次側に電圧を誘起させるものです。
つまり、変圧器には2種類の回路が存在しており、
- 2次側に交流電圧を誘導する回路(無負荷誘導電圧を誘起する回路)
- 電流負荷電流を流すための磁界を発生させる回路
が考えられます。
下の回路図は、変圧器のT型等価回路と言われており、計算は面倒ですが厳密性の高い等価回路です。
- 1次巻線インピーダンスは、変圧器の1次側巻線の銅線の抵抗や巻線のインダクタンス
- 2次巻線インピーダンスは、1次側のそれと同じ
- 励磁回路は、励磁のための回路
になります。
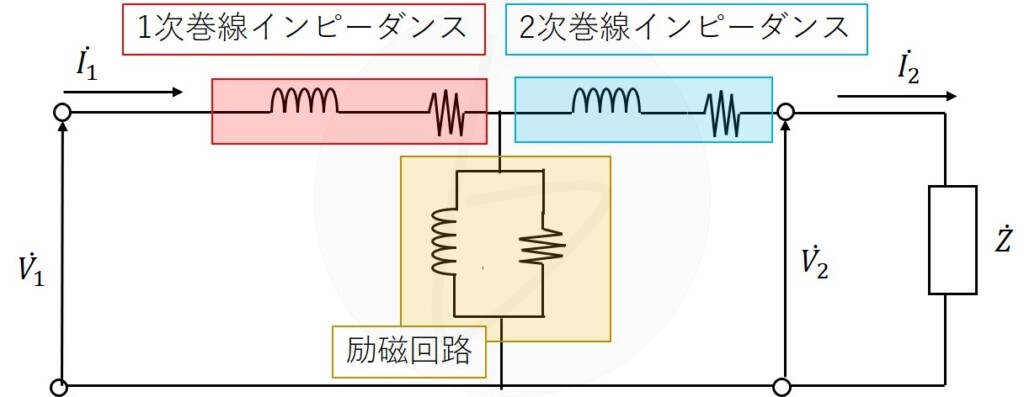
負荷Zがつながっていれば電流$I_2$が流れますが、2次側が開放されていれば、励磁回路に流れる励磁電流よって無負荷誘導起電力が現れます。
まさに、これが変圧器の動作そのものなのです。
これはすなわち、定格電圧≠無負荷誘導起電力を示しています。
定格電圧は、定格電流が流れているときに、無負荷誘導起電力から、2次側インピーダンスによる電圧降下をベクトル的に引いたものになります。
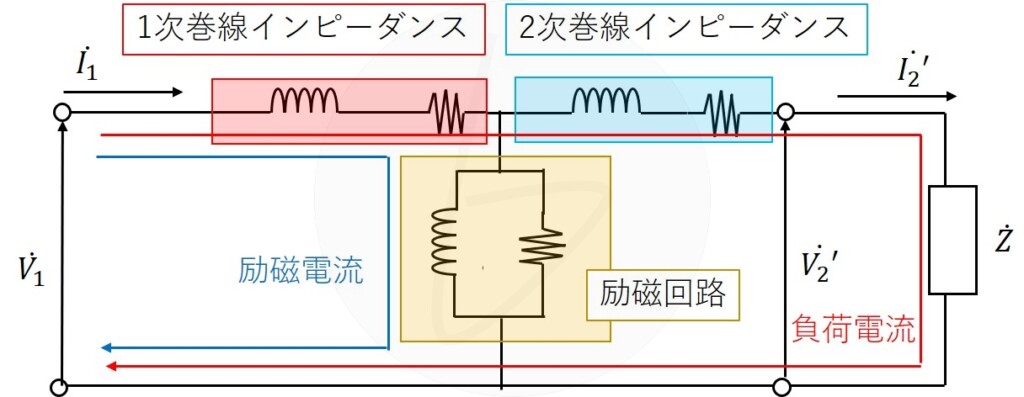
実用的なL型等価回路
変圧器の等価回路は以下の図のようになります。
励磁回路が、1次巻線よりも電源側に移動しています。
これにより、励磁回路と負荷電流の回路が完全に分断されるので、計算しやすくなります。
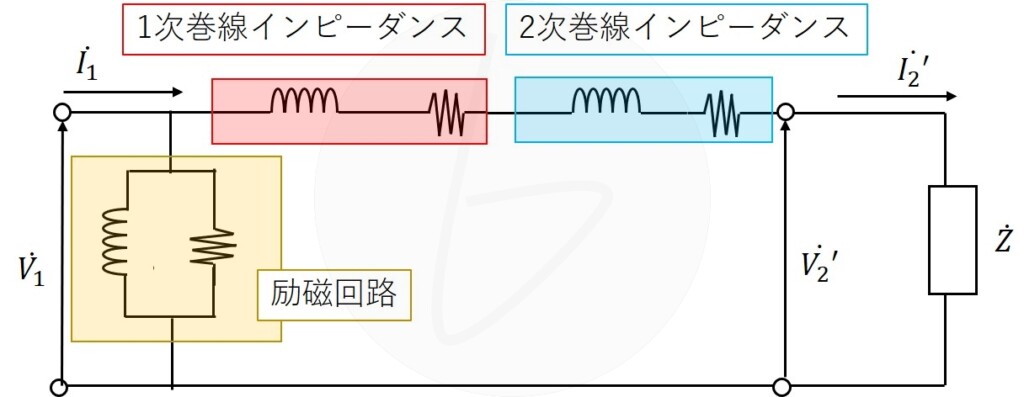
なお、L型等価回路は励磁回路の電流が非常に小さいことから、実用分においては特に問題とならない近似等価回路です。
電気主任技術者試験などでは、特に指定がない限りL型等価回路で計算できますし、問題によっては励磁電流については無視される場合もあります。
変圧器等価回路の1次側換算
さて、等価回路として1次側、2次側としてまとめるのであれば、電圧、電流が不整合になるので、何らかの補正が必要になります。
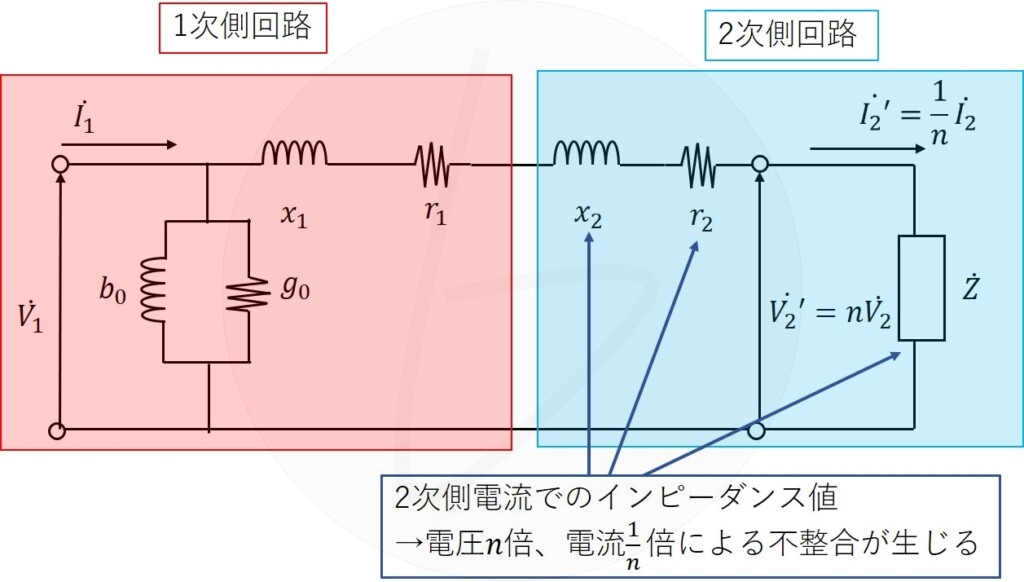
2次側のインピーダンスと電圧の関係は、オームの法則より、
$$V_2=Z_2 I_2$$
ですが、1次側に換算するため、
- $V_2=\frac{1}{n}V_1$
- $I_2=nI_1$
の関係があるので、
$$\frac{V_1}{n}=Z_2 nI_1$$
の関係になります。
これを整理すすと、
$$\frac{V_1}{I_1}=n^2 Z_2$$
となります。
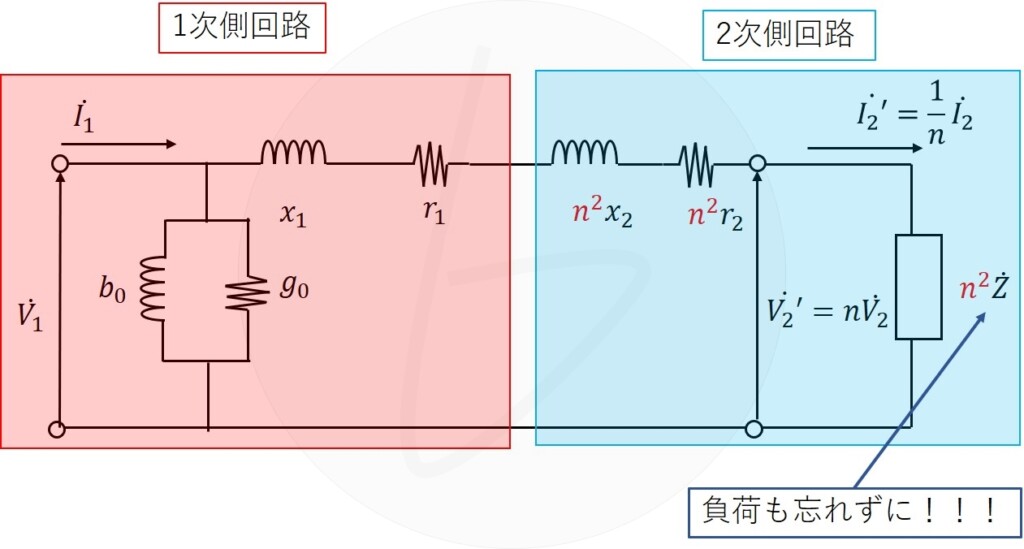
つまり、2次側のインピーダンスは、1次側からみると$n^2$倍されたように見えるので、変圧器の1次側に変換したL型等価回路は、以下のようになります。
ここまでできれば、あとは普通の電気回路の問題になります。
変圧器等価回路の2次側換算
変圧器のL型等価回路を2次側に換算してみましょう。
今度は、換算が必要になるのは、
- 1次側巻線インピーダンス
- 励磁回路
です。
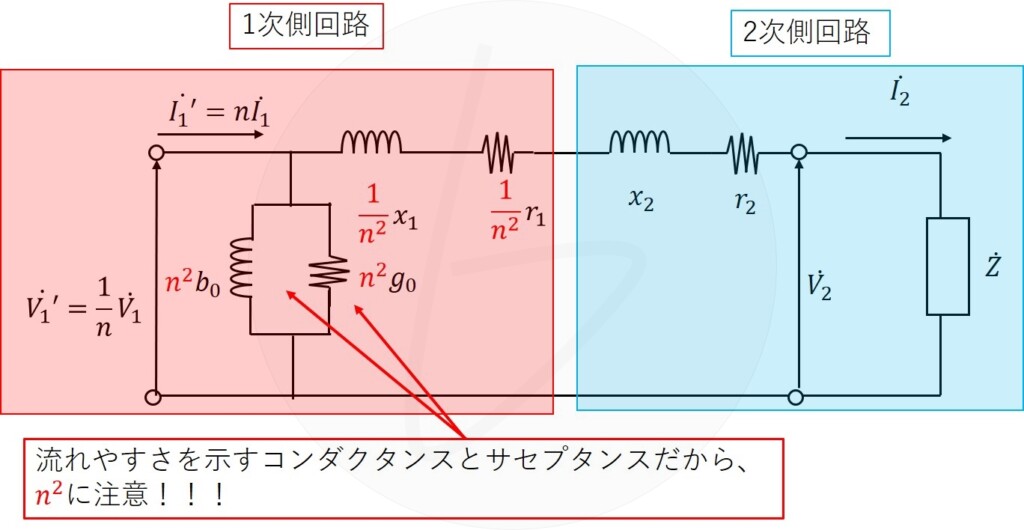
励磁回路は、通常の場合、流れやすさを示すコンダクタンスとサセプタンスで示されています。
インピーダンスとは逆の比率になるので気を付けてください。
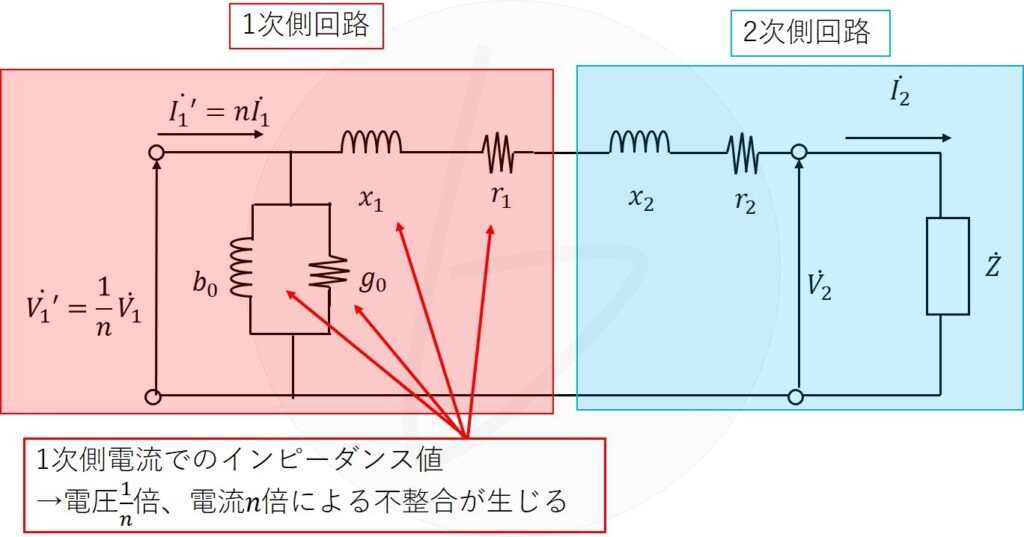
1次側回路はオームの法則より、
$$V_1=Z_1I_1$$
ですが、
- $V_1=nV_2$
- $I_1=\frac{1}{n}I_2$
より、
$$nV_2=Z_1\frac{I_2}{n}$$
となります。
しががって、
$$\frac{V_2}{I_2}=\frac{1}{n^2}Z_1$$
となるので、$\frac{1}{n^2}$が必要になります。
ここまでできれば、あとは電気回路のベクトル演算になります。
まとめ
ここまで、変圧器の等価回路において、一次側に換算する方法と二次側に換算する方法について紹介してきました。
変圧器を理解することは、誘導電動機を理解することにもなります。
換算という概念がなかなか分かりにくい部分ではありますが、電磁結合されている2つの回路を一つの回路として考えることができる便利な変換です。
また、より理解を深めるためには、単位法の概念も理解しておくといいでしょう。
以上、参考になれば幸いです。