みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、直流発電機の並行運転(並列運転)について説明します。
直流機の並行運転
循環電流を考慮する場合
直流発電機Aの負担する電流$I_a$、直流発電機Bの負担する電流$I_b$、直流発電機間の循環電流$I_{roop}$とすると、
$$\begin{cases}
I_a=\frac{r_b}{r_a+r_b}I+I_{roop}\\
I_b=\frac{r_a}{r_a+r_b}I-I_{roop}\\
I_{roop}=\frac{E_a-E_b}{r_a+r_b}
\end{cases} \tag{1}$$
となる。
ただし、
- $r_a$:直流発電機Aの電機子巻線抵抗
- $r_b$:直流発電機Bの電機子巻線抵抗
- $E_a$:直流発電機Aの誘導起電力
- $E_b$:直流発電機Bの誘導起電力
循環電流の方向は、直流発電機Aから直流発電機Bの方向に流れる向きを正としています。
詳しくは記事後半の導出でご確認ください。
循環電流を考慮しない場合
直流発電機Aの誘導起電力$E_a$と直流発電機Bの誘導起電力$E_b$において、$E_a=E_b$のとき、循環電流が流れず、
$$\begin{cases}
I_a=\frac{r_b}{r_a+r_b}I\\
I_b=\frac{r_a}{r_a+r_b}I
\end{cases} \tag{2}$$
となって、電機子巻線抵抗の逆比に従って負荷を分担する。
直流機の並行運転の導出
並行運転時の負荷分担の導出
直流発電機Aと直流発電機Bを並列に接続し、端子電圧$V$で負荷に電流$I$を供給している場合の回路図を図1に示します。
図1において、
- 直流発電機Aの負担する電流$I_a$
- 直流発電機Bの負担する電流$I_b$
を求めます。
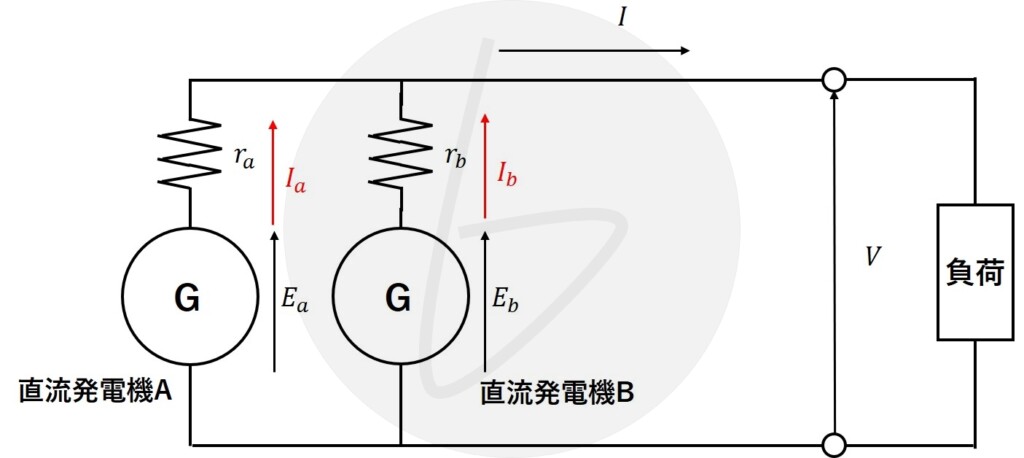
図1 直流発電機の並行運転
回路方程式より、
$$\begin{cases}
I=I_a+I_b\\
E_a=r_aI_a+V\\
E_b=r_bI_b+V
\end{cases} \tag{3}$$
となります。
この連立方程式から、$V$を消去するため、2つ目の式と3つ目の式の差を計算すれば、
$$E_a-E_b=r_aI_a-r_bI_b \tag{4}$$
となり、
$$I_b=\frac{r_a}{r_b}I_a-\frac{E_a-E_b}{r_b} \tag{5}$$
となります。
式()の一つ目の式に代入して、
$$I=I_a+\frac{r_a}{r_b}I_a-\frac{E_a-E_b}{r_b} \tag{6}$$
$$\frac{r_a+r_b}{r_b}I_a=I+\frac{E_a-E_b}{r_b} \tag{7}$$
$$I_a=\frac{r_b}{r_a+r_b}I+\frac{E_a-E_b}{r_a+r_b} \tag{8}$$
式()に代入して、
$$\begin{align}
I_b&=\frac{r_a}{r_b}\left( \frac{r_b}{r_a+r_b}I+\frac{E_a-E_b}{r_a+r_b}\right)-\frac{E_a-E_b}{r_b}\\
&=\frac{r_a}{r_a+r_b}I-\frac{E_a-E_b}{r_a+r_b} \tag{9}
\end{align}$$
となり、
$$\begin{cases}
I_a=\frac{r_b}{r_a+r_b}I+\frac{E_a-E_b}{r_a+r_b}\\
I_b=\frac{r_a}{r_a+r_b}I-\frac{E_a-E_b}{r_a+r_b}
\end{cases} \tag{10}$$
となります。
循環電流の導出
同期発電機の起電力$E_a$、$E_b$が異なる場合、図2に示す通り循環電流$I_{roop}$が流れます。
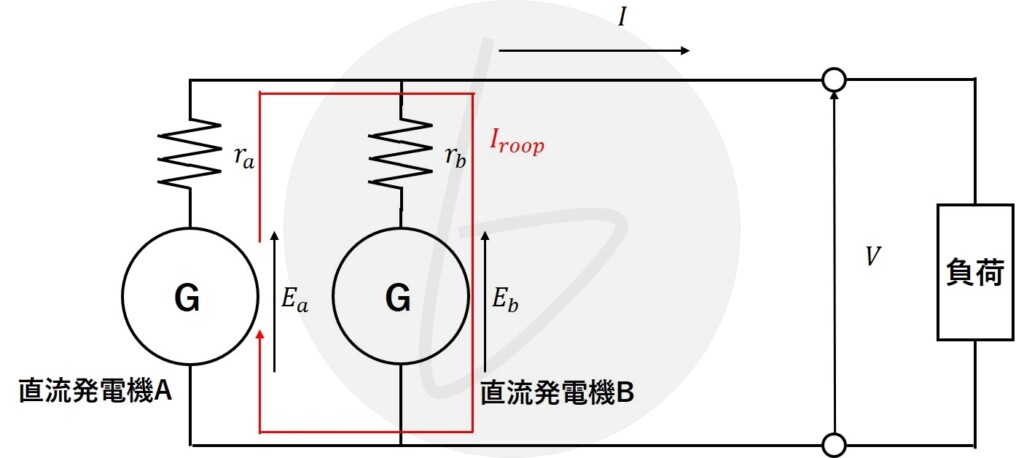
図2 直流発電機 並行運転時の循環電流
循環電流の経路において回路方程式を立式すれば、
$$E_a-E_b=I_{roop}(r_a+r_b) \tag{11}$$
であり、
$$I_{roop}=\frac{E_a-E_b}{r_a+r_b} \tag{12}$$
となります。
これより、式(10)は、
$$\begin{cases}
I_a=\frac{r_b}{r_a+r_b}I+I_{roop}\\
I_b=\frac{r_a}{r_a+r_b}I-I_{roop}\\
I_{roop}=\frac{E_a-E_b}{r_a+r_b}
\end{cases} \tag{13}$$
とも表記できます。
また、直流発電機Aの起電力$E_a$と直流発電機Bの起電力$E_b$において、
$E_=E_b$の関係があれば、$I_{roop}=0$となるので、直流発電機の負荷分担は、
$$\begin{cases}
I_a=\frac{r_b}{r_a+r_b}I\\
I_b=\frac{r_a}{r_a+r_b}I
\end{cases} \tag{14}$$
となって、単に電機子巻線抵抗の逆比に従って負荷電流を分担します。
まとめ
ここまで、直流発電機の並行運転(並列運転)について説明してきました。
直流回路の計算になるので、同期発電機の並行運転のようなややこしさはなく、計算も非常に単純です。
以上、直流発電機の並行運転(並列運転)について、参考になれば幸いです。