みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、変圧器の電圧変動率について説明します。
ベクトル図が登場するため、少しハードルが高いかもしれませんが、少しずつ読んでいってください。
前半では変圧器の回路図から、ベクトル図で電圧変動率を導出する流れになっています。
そのため、ベクトル図についての基本的な部分がご理解いただけてる場合、スムーズに読み進めることができるのではないかと思います。
▼おすすめ記事▼

電圧変動率とは?
電圧変動率$\epsilon$とは、
- 定格電圧:$V_{21}$
- 1次側電圧の2次側換算値:$V_{20}=\frac{V_1}{a}$
とすると、
$$\epsilon=\frac{V_{20}-V_{21}}{V_{21}}×100$$
となります。
これは、意味的には、
- 定格負荷が接続されているとき
- 負荷を切り離したとき
- 変圧器の端子に生じる電圧
と、定格電圧の比率ということです。
まず、定格状態の時には負荷電流$I_2$が流れているので、変圧器内部で電圧降下が生じています。
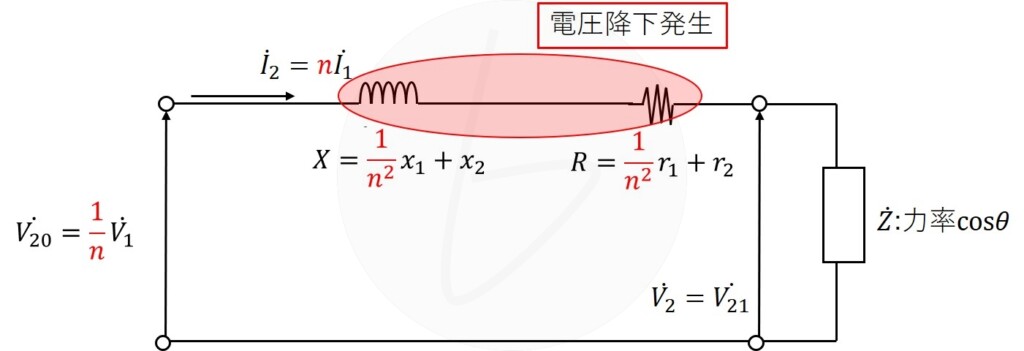
そして、無負荷になると負荷電流$I_2=0$になるので、変圧器内部での伝夏効果が生じません。
その結果、2次側端子に$V_{20}$がそのまま表れることになります。
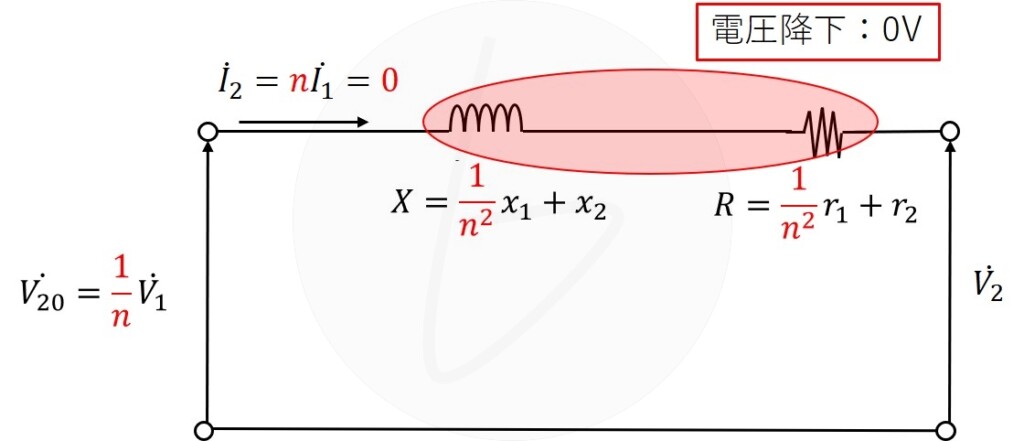
この無負荷時の電圧が、2次側定格電圧に対してどの程度の大きさであるかを示すものが、電圧変動率になります。
つまり、電圧変動率は
- 2次側巻線のインピーダンス値が大きい変圧器ほど
- 定格負荷電流の大きい変圧器ほど
電圧変動率も大きくなることがわかります。
試験問題などでは、単に電圧変動率を求めることや、電圧変動率を利用した計算を行うことが多いです。
なお、実際に電力系統で変圧器が使用される場合、電圧変動率は小さいほうが好まれる傾向にあるそうです。
電圧変動率のベクトル図からの導出
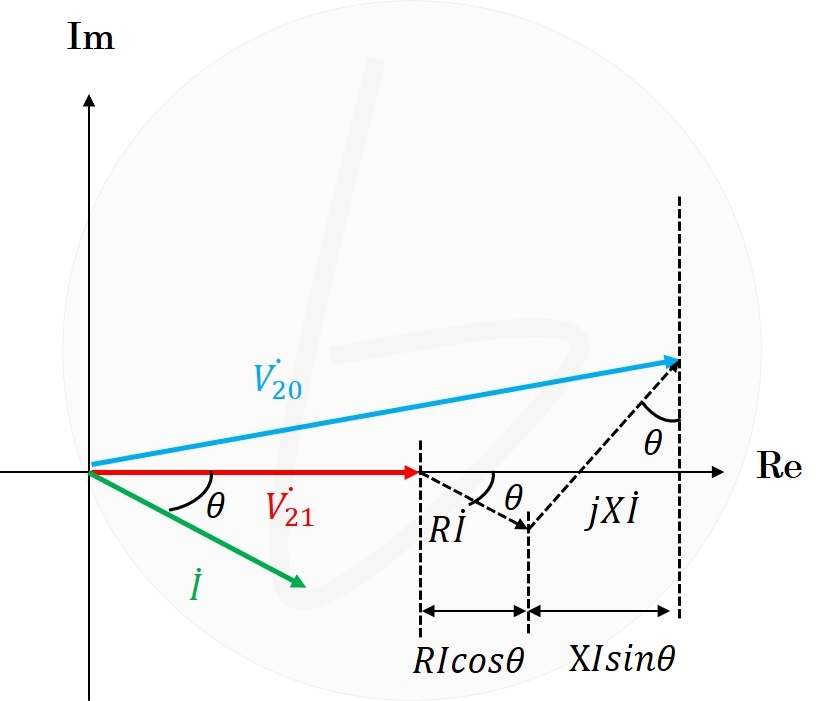
回路図より、定格電圧$V_{21}$と無負荷誘導起電力$V_{20}$、定格電流$I$の関係をベクトル図で表すと、下のようになります。
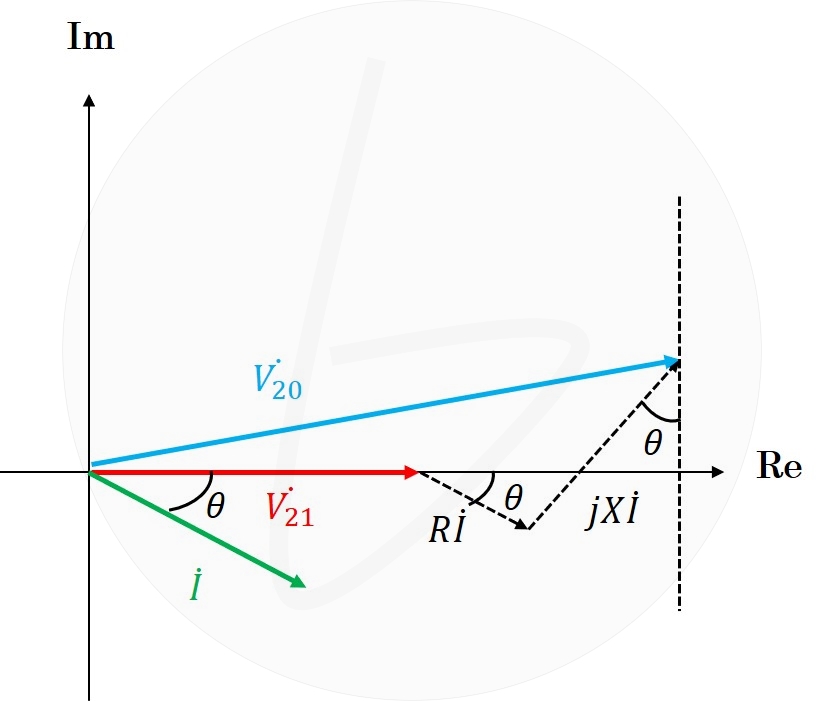
ここで等式を立てていきます。
まず、実軸成分に注目すると、下の図より、
$$V_{20}の実軸成分=V_{21}+RIcos\theta+XIsin\theta$$
が成り立ちます。
次に、虚軸成分に注目すると、
$$V_{20}の虚軸成分=RIcos\theta-XIsin\theta$$
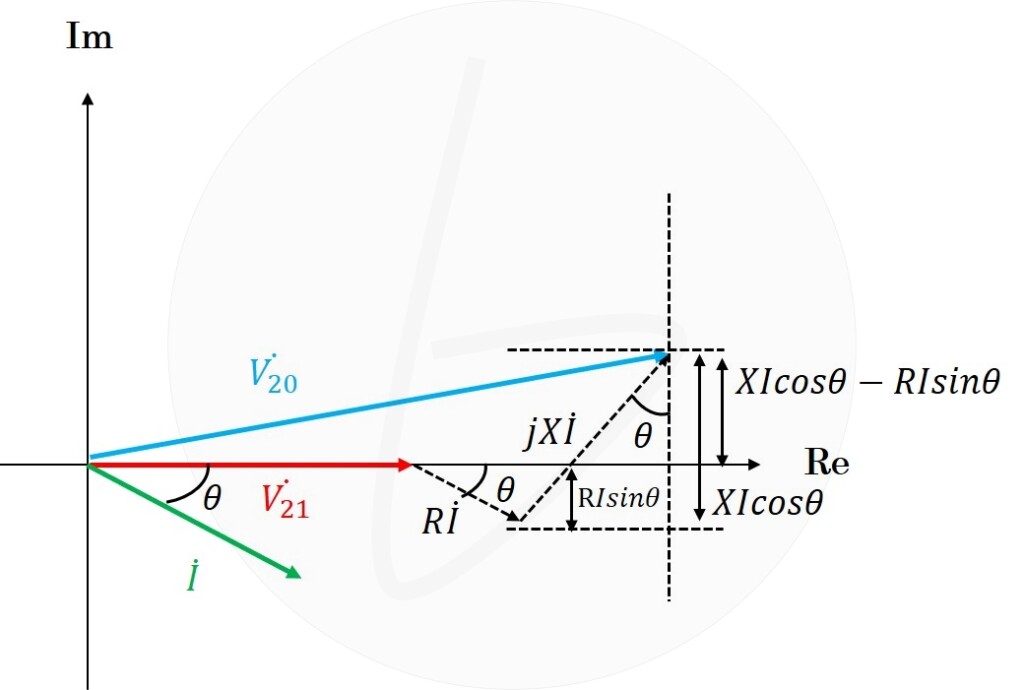
これより、三平方の定理から、
$${V_{20}}^2=(V_{21}+RIcos\theta+XIsin\theta)^2+(XIcos\theta-RIsin\theta)^2$$
となります。
両辺を${V_{21}}^2$で割ると、
$${(\frac{V_{20}}{V_{21}}})^2=(1+\frac{RI}{V_{21}}cos\theta+\frac{XI}{V_{21}}sin\theta)^2+(\frac{XI}{V_{21}}cos\theta-\frac{RI}{V_{21}}sin\theta)^2$$
ここで、パーセント抵抗を$p$[%], パーセントリアクタンスを$x$[%]とすると、
- $p=\frac{RI}{V_{21}}×100$
- $x=\frac{XI}{V_{21}}×100$
より、
$${(\frac{V_{20}}{V_{21}}})^2=(1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta)^2+(\frac{q}{100}cos\theta-\frac{p}{100}sin\theta)^2$$
$${(\frac{V_{20}}{V_{21}}})^2=(1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta)^2(1+(\frac{\frac{q}{100}cos\theta-\frac{p}{100}sin\theta}{1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta})^2)$$
$$\frac{V_{20}}{V_{21}}=(1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta)\sqrt{(1+(\frac{\frac{q}{100}cos\theta-\frac{p}{100}sin\theta}{1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta})^2)}$$
ここで、$\sqrt{1+x^2}≒1+\frac{1}{2}x^2$より、
$$\frac{V_{20}}{V_{21}}=(1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta)(1+\frac{1}{2}(\frac{\frac{q}{100}cos\theta-\frac{p}{100}sin\theta}{1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta})^2)$$
$$\frac{V_{20}-V_{21}}{V_{21}}=1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta+\frac{1}{2}\frac{(\frac{q}{100}cos\theta-\frac{p}{100}sin\theta)^2}{1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta}$$
$\frac{V_{20}-V_{21}}{V_21}=\frac{V_{20}}{V_{21}}-1$より、
$$\frac{V_{20}-V_{21}}{V_{21}}=\frac{p}{100}cos\theta+\frac{q}{100}sin\theta+\frac{1}{2}\frac{(\frac{q}{100}cos\theta-\frac{p}{100}sin\theta)^2}{1+\frac{p}{100}cos\theta+\frac{q}{100}sin\theta}$$
$$\frac{V_{20}-V_{21}}{V_{21}}≒\frac{p}{100}cos\theta+\frac{q}{100}sin\theta+\frac{1}{2}(\frac{q}{100}cos\theta-\frac{p}{100}sin\theta)^2$$
となります。
最終的に、
$$\epsilon=\frac{V_{20}-V_{21}}{V_{21}}×100$$
なので、
$$\epsilon=\frac{V_{20}-V_{21}}{V_{21}}×100=pcos\theta+qsin\theta+\frac{(qcos\theta-psin\theta)^2}{200}$$
となります。
一般的には、右辺第2項は小さいため無視できて、
$$\epsilon=\frac{V_{20}-V_{21}}{V_{21}}×100=pcos\theta+qsin\theta$$
で使われることが多いです。
まとめ
ここまで、変圧器の電圧変動率について説明してきました。
一見難しそうな計算ですが、電圧変動率の意味するところを理解してしまえば、あとはベクトル図から求まります。
特にベクトル図についても、三平方の定理で計算できるシンプルなものですから、sin,cosの取り方だけ間違えないようにすれば、スムーズに計算できるでしょう。
以上、変圧器の電圧変動率について、参考になれば幸いです。