みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は変圧器の並列運転についてです。
変圧器の並列運転は、
- 負荷電流の分担
- 循環電流
がポイントになります。
▼おすすめ記事▼

変圧器の負荷電流分担の計算方法の導出
負荷電流分担の基本的な式
前提条件として、
- 一次印加電圧:$V_1$[V]
- 2次側巻数:$N_A$, $N_B$
- 変圧器のインピーダンス:$Z_A$, $Z_B$
とします。
一次側の励磁回路を無視すると、変圧器の並列運転の等価回路は、以下の図になります。
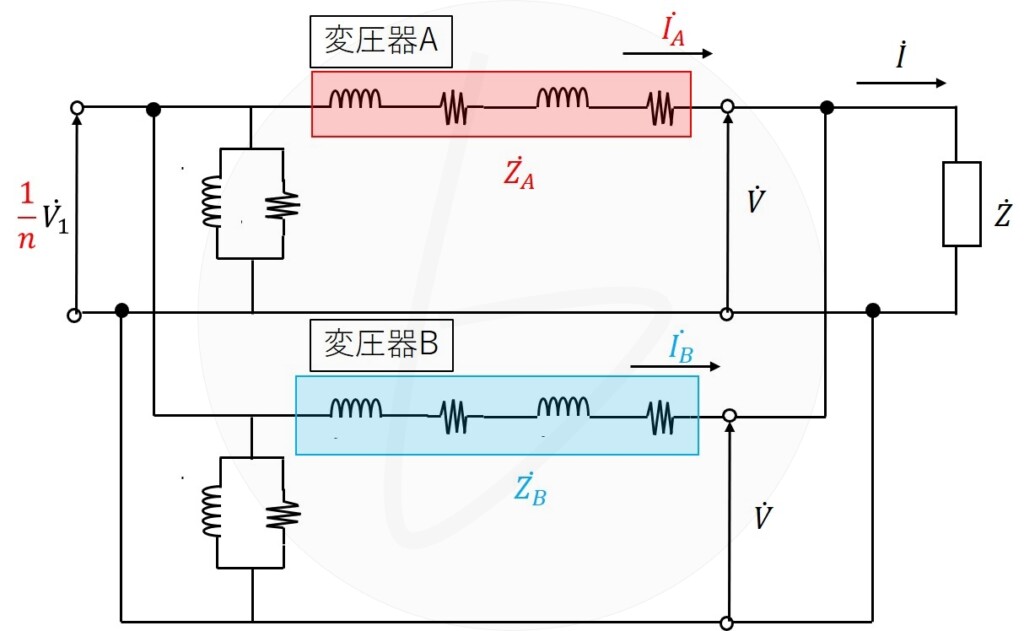
これをもう少し見やすくします。
具体的には、1次入力電圧を交流電圧源に置き換えます。
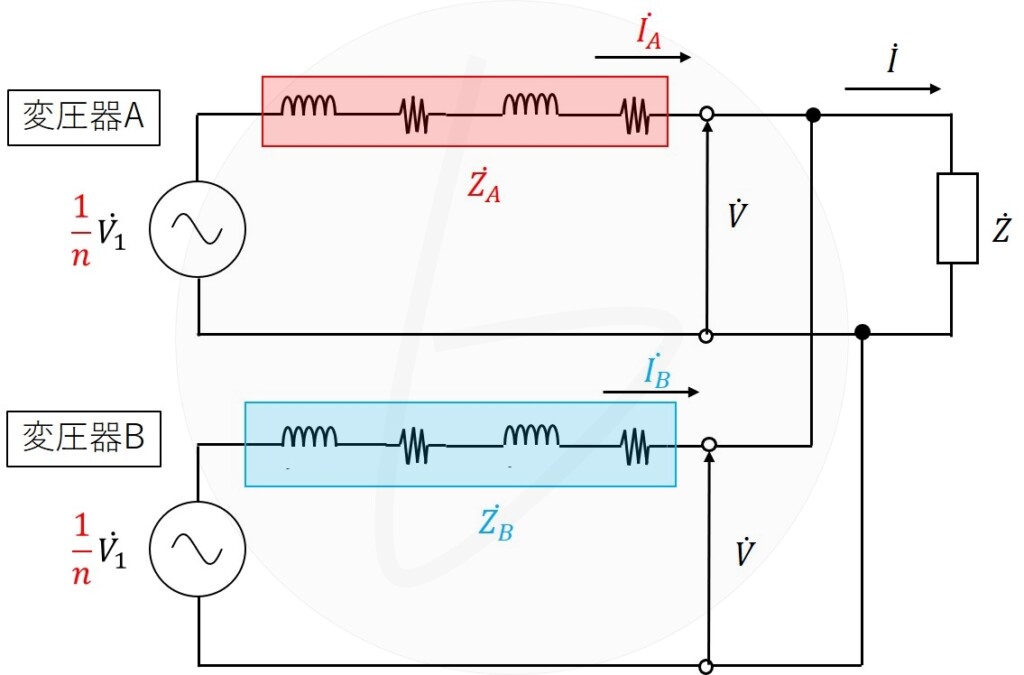
これで負荷電流の分担が計算できます。
2次側電圧を$V$で共通とすると、オームの法則より
$$\frac{1}{n}\dot{V_1}-\dot{V}=\dot{Z_A}\dot{I_A}$$
$$\frac{1}{n}\dot{V_1}-\dot{V}=\dot{Z_B}\dot{I_B}$$
これより、
$$\dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_B}}\dot{I_A}$$
となります。
またキルヒホッフの第1法則より、
$$\dot{I}=\dot{I_A}+\dot{I_B}$$
より、
$$\dot{I}=\dot{I_A}+\frac{\dot{Z_A}}{\dot{Z_B}}\dot{I_A}$$
より、
$$\dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}$$
$$\dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}$$
となります。
これが、変圧器の負荷分担において基本となる式です。
循環電流を考慮する場合
では、巻数比の異なる2つの変圧器が並列接続された場合を考えます。
起電力がことなる電源が2つつながることになるので、当然循環電流が流れます。
循環電流の経路は、下の回路図に示すとおりになります。
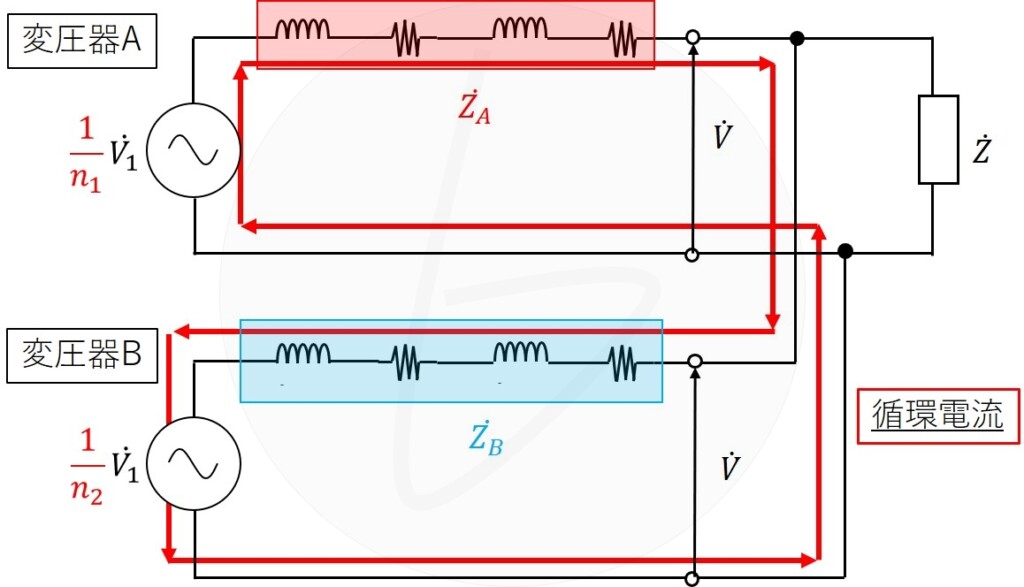
さて、これで循環電流が計算できます。
循環電流を$\dot{I_{roop}}$とおき、赤の矢印の電流経路を正にすると、オームの法則(キルヒホッフの第2法則と考えたほうが正確かも)から、
$$\frac{1}{n_1}\dot{V_1}=(\dot{Z_A}+\dot{Z_B})I_{roop}+\frac{1}{n_2}\dot{V_1}$$
となります。
これより、循環電流$I_{roop}$は、
$$\dot{I_{roop}}=\frac{\frac{1}{n_1}-\frac{1}{n_2}}{\dot{Z_A}+\dot{Z_B}}\dot{V_1}$$
となります。
さて、負荷電流の電流経路と合わせると、電流経路は下の回路図のようになります。
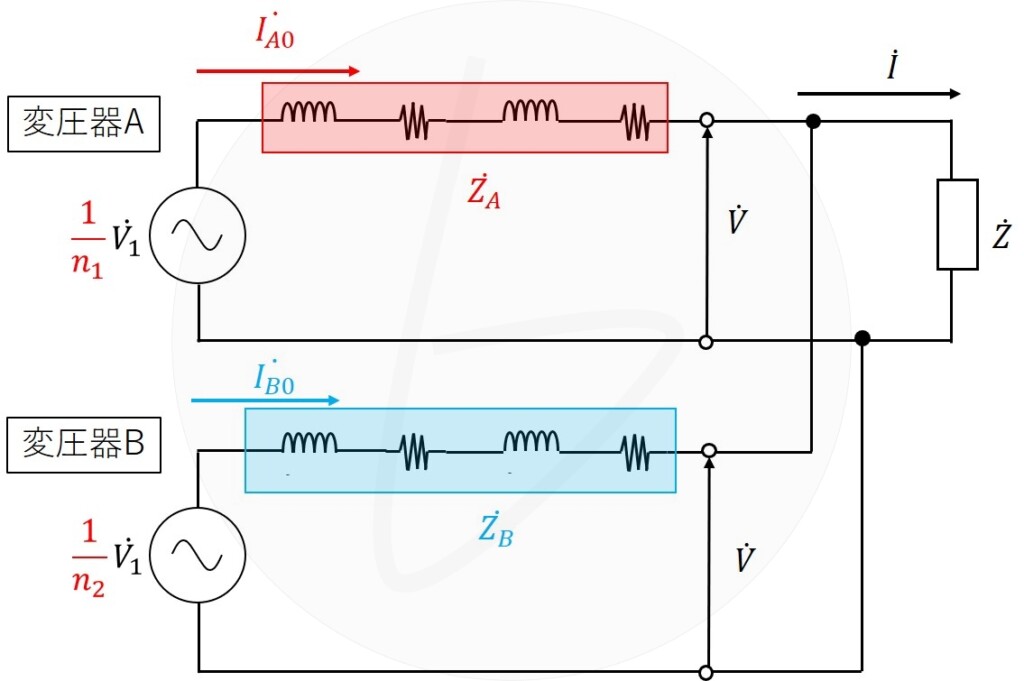
つまり、変圧器Aは負荷電流+循環電流、変圧器Bは負荷電流-循環電流となるので、
$$変圧器Aの負担=\dot{I_A}+\dot{I_{roop}}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}+\frac{\frac{1}{n_1}-\frac{1}{n_2}}{\dot{Z_A}+\dot{Z_B}}\dot{V_1}$$
$$変圧器Bの負担=\dot{I_A}-\dot{I_{roop}}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}-\frac{\frac{1}{n_1}-\frac{1}{n_2}}{\dot{Z_A}+\dot{Z_B}}\dot{V_1}$$
となります。
まとめ
ここまで、変圧器の並列運転について説明してきました。
一見ややこしそうに見える変圧器ですが、交流の起電力として考えてしまえば、あとは普通の交流回路の計算にまで落とし込めます。
循環電流についても、巻数比の違いからくる起電力の違いを考えれば、自然に導出ができるでしょう。
以上、変圧器の並列運転について、参考になれば幸いです。