みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、自動制御の二次遅れ系について説明していきます。
二次遅れ系の式
自動制御の分野で主要な項目になる、二次遅れ要素についてみていきます。
この二次遅れ要素には、共振という特徴的な性質があり、第1種および第2種 電気主任技術者試験 2次試験での出題頻度も非常に高いです。
二次遅れ要素の伝達関数は、式(1)で示されます。
$$G\left(s\right)=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2} \tag{1}$$
式(1)において、
- $\xi$:減衰係数
- $\omega_n$:固有角周波数
と呼びます。
式(1)は「式の構造」必ず覚えてください。
特に電験2次試験の試験問題で、伝達関数を導いた後、「減衰係数$\xi$、固有角周波数$\omega_n$を求めよ。」と問う問題、および関連問題が頻出です。
こうした問題は、知っていれば解けるサービス問題です。
二次遅れ系の極と応答波形の概要
伝達関数の、分母=0となる$s$の値のことを、伝達関数の極といいます。
伝達関数を逆ラプラス変換するとき、部分分数分解によって既知のラプラス変換の形まで変形しますが、この時、分母を因数分解していました。
ここで、
$$\begin{matrix}
\mathcal{L}\left[e^{-at}\right]=\frac{1}{s+a} & \rightarrow & 極s=-a
\end{matrix}\tag{2}$$
$$\begin{matrix}
\mathcal{L}\left[cos\ \omega t\right]=\frac{1}{s^2+\omega^2} & \rightarrow & 極s=±j\omega
\end{matrix}\tag{3}$$
$$\begin{matrix}
\mathcal{L}\left[sin\ \omega t\right]=\frac{\omega}{s^2+\omega^2} & \rightarrow & 極s=±j\omega
\end{matrix}\tag{4}$$
となるので、極が虚数解を持つかどうかで、三角関数の振動があるかないかを見分けることができます。
二次遅れ要素は、こうした振動の有無について、減衰係数\xiの値によって、
- 極が実数解となるか
- 極が重解となるか
- 極が虚数解となるか
の場合分けして、詳細を見ていきます。
極による応答波形の違い
インパルス応答
インパルス応答は、$X\left(s\right)$にインパルス的な信号が入り、0に戻る場合です。
ノイズみたいな外乱が瞬間的に入ったときに、どんな挙動を示しながら0に戻るかです。
この時、制御系はすぐに0位置に戻ってきてほしいのですが、減衰係数や固有角周波数から計算される$\xi$の値によって、以下のような応答波形になります。
ここで、
- 橙:$\xi<1$(不足減衰)
- 緑:$\xi=1$(臨界減衰)
- 赤:$\xi>1$(過減衰)
です。
臨界減衰の時、出力は最も早く0位置に戻ります。
$\xi$の値が小さく、$\xi<1$の時不足減衰となり、振動しながら0位置に戻ります。
逆に$\xi$の値が大きく、$\xi>1$の時は過減衰となり、振動はしませんが、なかなら0位置に戻ってきません。
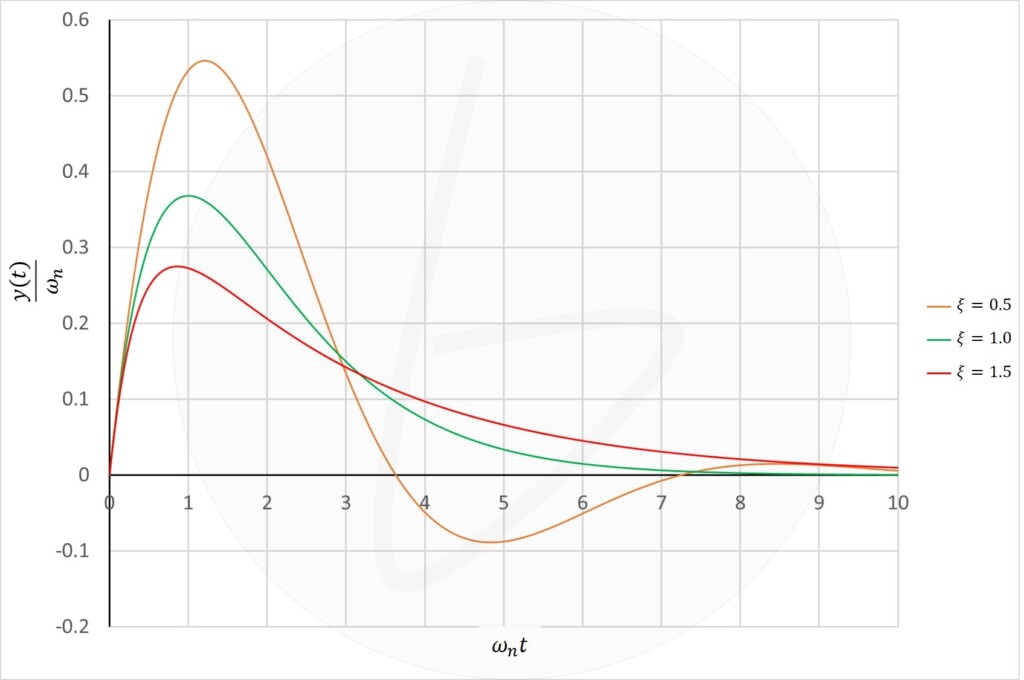
図2 二次遅れ系のインパルス応答
単位ステップ応答(インディシャル応答)
単位ステップ応答(インディシャル応答)は、入力信号が$X\left(s\right)$が0→1へ、ステップ状に変化した状況を想定しています。
この時、制御系はすぐに目標値に追従してほしいのですが、減衰係数や固有角周波数から計算される$\xi$の値によって、以下のような応答波形になります。
ここで、インパルス応答の時と同じで、
- 橙:$\xi<1$(不足減衰)
- 緑:$\xi=1$(臨界減衰)
- 赤:$\xi>1$(過減衰)
です。
臨界減衰の時、最も早く収束します。
$\xi$の値が小さく、$\xi<1$の時不足減衰となり、振動しながら収束します。
逆に$\xi$の値が大きく、$\xi>1$の時は過減衰となり、振動はしませんが、収束も遅くなります。
.jpg)
図3 二次遅れ系の単位ステップ応答(インディシャル応答)
まとめ
ここまで、
- 二次遅れ系の式
- 二次遅れ系における応答波形の概要
について説明してきました。
以上、二次遅れ系について参考になれば幸いです。
●紙の本:3,850円(税込)
電験2種 二次試験 機械・制御で出題される自動制御を完答することを目的に作成した参考書。
機械・制御において、自動制御で満点を狙い、確実に合格したい場合には、この参考書がおすすめです。