みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、誘導電動機で重要になる、比例推移について紹介します。
そして、比例推移とセットで登場する、トルクと滑りの線形関係を利用した問題の解法について紹介します。
比例推移の問題の最大のポイントは、2次側の特性のみですべてが解けることです。
- 比例推移
- トルクが滑りに比例
の関係さえあれば、1次側回路の情報が一切なくても問題が解けてしまう。
これは、比例推移をしっかりと理解しているかを問うことができる問題(比例推移を理解していなければ実質的に回答は不可能)なので、電気主任技術者試験では定番の問題といえます。
▼おすすめ記事▼
誘導電動機の比例推移
比例推移の使える計算
誘導電動機の特性計算については、等価回路の導出も含めて以下の記事で説明しました。
その時に紹介した三相誘導電動機の特性式が、以下のものになります。
■2次電流$I_2’$
$$I_2´=\frac{V}{\sqrt{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)^2}} \tag{1}$$
■2次入力$P_2$(回転子に加わるエネルギー)
$$P_2=3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}\frac{1}{s}r_2´ \tag{2}$$
■トルク$T$
$$T=\frac{1}{\omega_0}3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}\frac{1}{s}r_2´ \tag{3}$$
比例推移が使える特徴として、これらすべての特性式に、$\frac{r_2´}{s}$が含まれていることがあります。
回転数によって滑り$s$が変化しますが、同じ比率で$r_2´$を変化させれば、誘導電動機の特性値はすべて一定になります。
例えば一定トルクで加速させたい場合、始動時は滑りが大きい($s=1$)ので、二次抵抗$r_2’$もそれに合わせて大きくします。
回転数が上昇すると滑りが小さくなり($s=1→0$)、滑りの減少率と一緒に2次抵抗$r_2’$を小さくすれば、常に$\frac{r_2′}{s}$が一定になるので、一定トルクで同期速度まで加速します。
以上のように、滑りが変化したとき、同じ比率で2次側抵抗$r_2´$を変化させることで、回転数が異なっても式(1)~式(3)の特性を全く同じにできるのが「比例推移」です。
なお、比例推移が利用できるのは巻線型誘導電動機のみです。
かご型誘導電動機では2次抵抗を可変にできないため、比例推移の制御は不可能です。
今現在の技術としては、一般的にはインバーターで交流電源の周波数を可変でき、つまり誘導電動機の駆動中に滑り周波数を可変にできます。
そのため、2次抵抗を可変にできない かご形誘導電動機でも、電源周波数を制御し、滑り周波数を制御する意味の比例推移は可能です。
比例推移を使えない計算
機械出力や2次銅損については比例推移は適用できません。
■機械出力
$$P_o=3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}\frac{1-s}{s}r_2´ \tag{4}$$
機械的出力では、$\frac{1-s}{s}r_2´$の項があるため、係数$1-s$の変化を$r_2´$の変化で吸収できないためです。
比例推移では、滑り$s$が大きくなれば同じ比率で2次抵抗$r_2’$を大きくするため、滑りが大きい時には$\frac{1-s}{s}r_2’$が小さくなり、機械出力$P_o$は小さくなります。
■2次銅損$P_2$
$$P_2=3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}r_2´ \tag{5}$$
2次銅損については、$r_2’$が単独で乗算されているので、二次抵抗を大きくすればその分2次銅損も大きくなります。
これは直感的なエネルギーフローの関係性ともよく合います。
トルクを得るために2次抵抗が増えれば、それと同時に2次側銅損が増える、つまり誘導電動機に入力されたエネルギーの多くが熱に変換されることになります。
入出力間で総エネルギーは保存されますから、銅損の増加に伴い機械出力は低下するため、これらに対して比例推移は適用できません。
ちょっとややこしいですが、式(2)、式(4)、式(5)において、
$${\rm 2次入力}P_2={\rm 機械出力}P_o+{\rm 2次銅損}P_2$$
となり、出力と銅損の和である2次入力$P_2$には比例推移が適用できます。
トルクと滑りの比例関係
近似的にですが、滑りが十分小さい場合においては、トルクと滑りは比例します。
これは近似的なものであり、特性として覚える必要もあまりないように思いますが、稀に問われることがあるので知っておいて損はないといった範囲の話でしょう。
トルクと滑りの比例関係を利用する場合、基本的に問題文には記載されているように思います。
ただ、何も知らずに問題文を読むと意味不明になるので、事前にそんなもんなんだと知っておくことは大切でしょう。
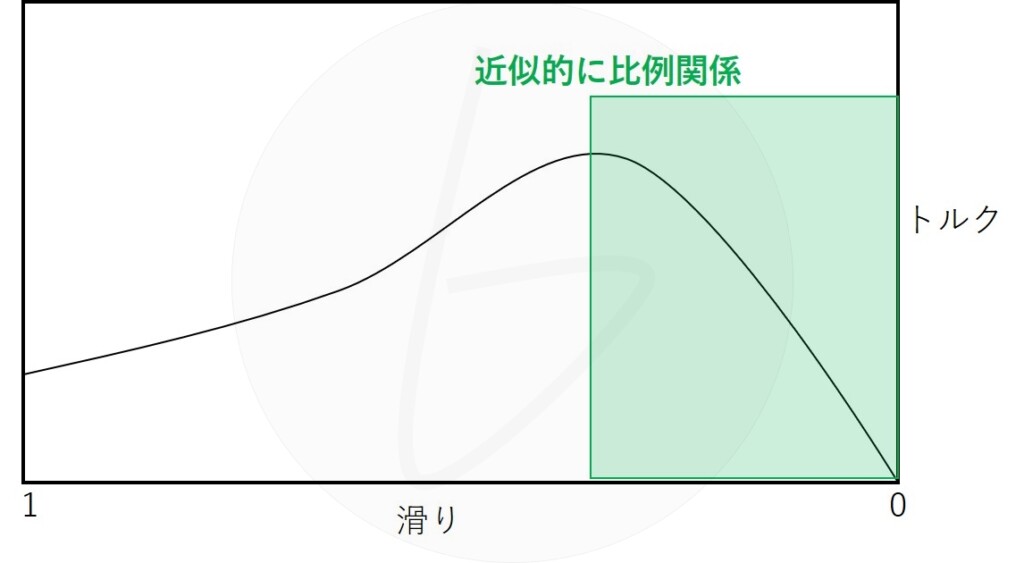
図1 誘導電動機のトルクと滑りのの比例関係($s=1$付近で近似的に成立)
何度も書きますが、トルクと滑りの比例関係は、単なる近似的な特性です。
比例推移の例題を考える
では、例題を考えてみましょう。
■■■例題■■■
定格周波数 60[Hz], 6極の巻線型三相誘導電動機がある。この電動機の
2 次側巻線は Y 結線で、1 相の抵抗値は 0.034[Ω]である。今、負荷につな
がって $1000{\rm\left[min^{−1} \right]}$で安定して回転している。
この時、各設問に答えよ。
(1)同期速度を求めよ。
(2)滑りを求めよ
回転数を$800{\rm \left[min^{−1} \right]}$に下げたい場合を考える。
ただし、負荷トルクは回転速度に比例するものとする。
(3)$800{\rm \left[min^{−1} \right]}$での負荷トルクは$1000{\rm \left[min^{−1} \right]}$時の何倍か計算せよ
(4)2 次側に挿入する 1 相当たりの抵抗値を求めよ。ただし、滑りとトル
クは比例関係にあるものとする。
■■■回答・解説■■■
(1)
同期速度$N_0$は、
$$N_0=\frac{120}{p}f=\frac{120}{6}×60=1200{\rm \left[min^{-1}\right]} \tag{解1}$$
となる。
(答)$N_0=1200\left[{\rm min^{-1}}\right]$
(2)
$1000{\rm \left[min^{-1}\right]}$のときの滑り$s_{1000}$は、
$$s_{1000}=\frac{N_0-N}{N_0}=\frac{1200-1000}{1200}=0.16666666666 \tag{解2}$$
となる。
(答)$s=0.167$
(3)
負荷トルクは速度に比例するので、誘導機の回転速度が$800{\rm \left[min^{-1}\right]}$のとき、
$$\frac{800}{1000}=0.8{\rm 倍} \tag{解3}$$
となる。
(答)0.800倍
(4)
小問(3)において、$800{\rm \left[min^{-1}\right]}$のときに必要なトルクは0.8倍である。
そして、解図1に示す通り、滑りとトルクの直線近似を利用すれば、$800{\rm \left[min^{-1}\right]}$のときに必要なトルクを生じさせる滑り$s_{800}’$は、二次抵抗を変更しない場合、
$$s_{800}’=s_{1000}×0.8=0.16666666666×0.8=0.13333333332 \tag{解4}$$
のときに発生する。
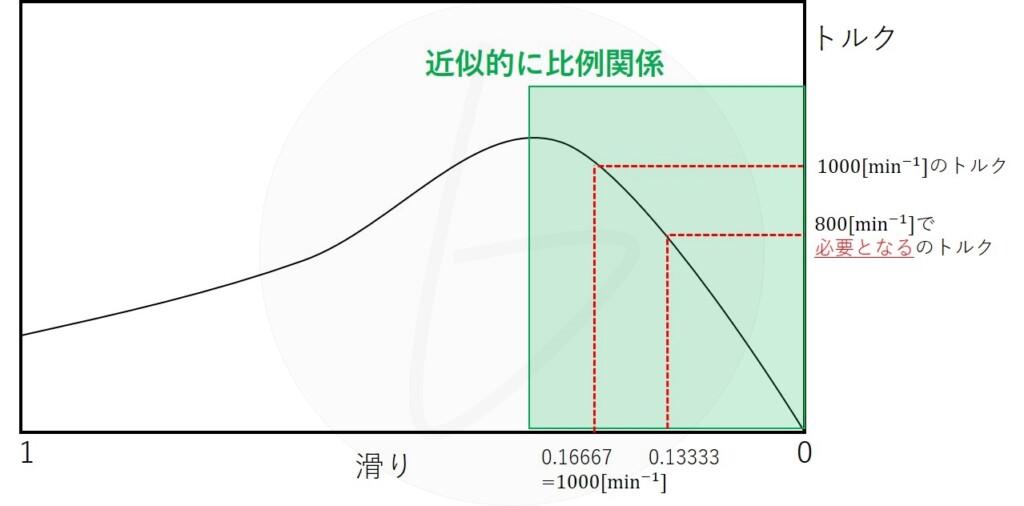
解図1 $1000\left[{\rm min^{-1} }\right]$と$800\left[ {\rm min^{-1}} \right]$における必要なトルクと2次抵抗挿入前の誘導機の滑り
また、$800{\rm \left[min^{-1}\right]}$のときの滑り$s_{800}$は、
$$s_{800}=\frac{1200-800}{1200}=0.33333333333 \tag{解5}$$
である。
以上より、本来は滑り式(解4)の$s_{800}’$のときに生じるトルクを、式(解5)の滑り$s_{800}$のときに生じさせたい。
つまりトルクをそのままに滑りを変えるので比例推移そのものであり、比例推移を適用した際の二次抵抗は、
$$\frac{s_{800}}{s_{800}’}r_2’=\frac{0.33333333333}{0.13333333332}×0.034=0.085{\rm \left[Ω\right]} \tag{解6}$$
となる。
なお、もともと0.034[Ω]の抵抗があるので、挿入する抵抗はこの分を減算して、
$$0.085-0.034=0.051\rm{\left[Ω\right]} \tag{解7}$$
となる。
(答)0.0510[Ω]
まとめ
ここまで、誘導電動機の比例推移について説明してきました。
誘導電動機の比例推移は、誘導電動機のトルクと滑りの比例関係と絡めて出題されることが多いです。
少し問題を解く際の順序がややこしいですが、
ある回転数の時に得たいトルク
と、2次抵抗を挿入せずに、
得たいトルクを得られるように回転数だけを調整した際の滑り
を計算すれば、それらの滑りの比率が2次抵抗の比率になります。
慣れれば難しいことはないので、順に計算してみてください。
以上、誘導電動機の比例推移と、トルクと滑りの比例関係を利用する問題の解法について、参考になれば幸いです。