みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、最終値の定理を使ったフィードバック制御系の定常偏差の計算方法と、前向き伝達関数に積分要素を追加することで定常偏差を0にする設計手法について説明します。
フィードバック制御系の目的や身近な例を知りたい方は、以下の記事をご覧ください。
偏差と定常偏差
フィードバック制御系における
$$E\left(s\right)=R\left(s\right)-Y\left(s\right)\tag{1}$$
を偏差といいます。
フィードバック制御系では、偏差が0になるように絶えず制御を行っていますが、目標値$X\left(s\right)$が変化してから十分時間が経っても、偏差が残り続ける場合があり、これを定常偏差といいます。
定常偏差は、偏差に対して最終値の定理を適用すれば求めることができ、
$$e\left(\infty\right)=\lim_{s→0}{sE\left(s\right)}\tag{2}$$
と計算することが可能です。
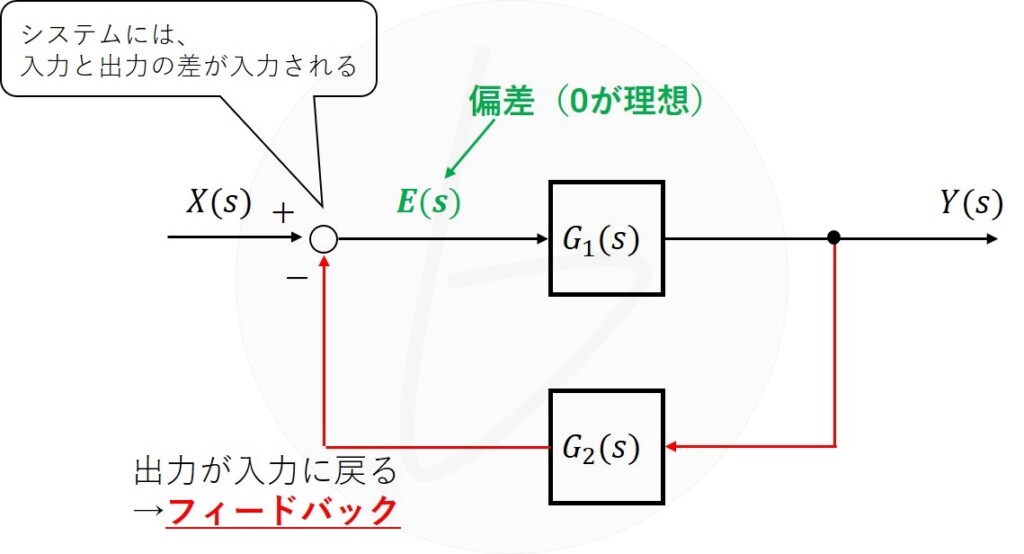
図1 フィードバック制御系の偏差
定常偏差は0であることが望ましいが、必ずしも0になるとは限りません。
次に示すように、一般的に、制御ブロック(前向き伝達関数)に積分器を挿入すれば、定常偏差を0にすることが可能です。
定常偏差と積分要素
図2に一般的なフィードバック制御系のブロック線図を示します。
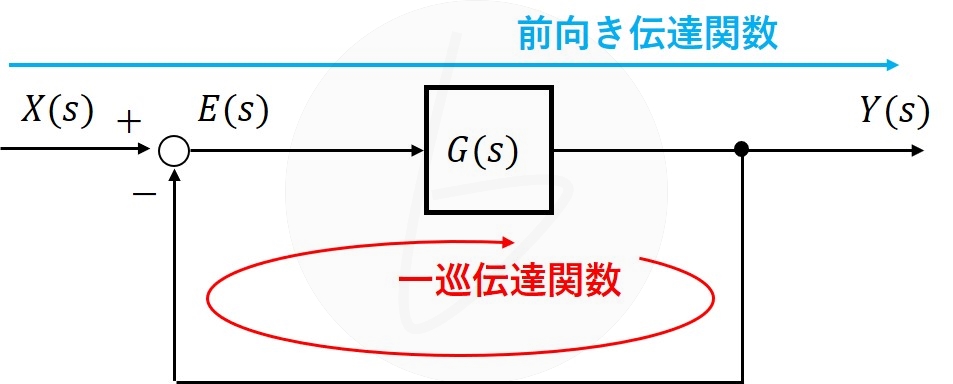
図2 一般的なフィードバック制御系のブロック線図
前向き伝達関数$G\left(s\right)$が存在する時、
$$Y\left(s\right)=\frac{G\left(s\right)}{1+G\left(s\right)}R\left(s\right)\tag{3}$$
であるから、
$$E\left(s\right)=R\left(s\right)-Y\left(s\right)=\frac{1}{1+G\left(s\right)}R\left(s\right)\tag{4}$$
となります。
この時定常偏差にある値が残るとすれば、
$$\begin{align}
e\left(\infty\right)&=\lim_{s→0}sE\left(s\right)\\
&=\lim_{s→0}s\frac{1}{1+G\left(s\right)}R\left(s\right)\\
&=\lim_{s→0}s\frac{1}{1+G\left(s\right)}\frac{1}{s}\\
&=\lim_{s→0}\frac{1}{1+G\left(s\right)}\tag{5}
\end{align}$$
ここで、式()が$s→0$のときに0とするには、$G\left(s\right)→\infty$となればいいです。
ここで、直感的イメージとして、$G\left(s\right)$が積分要素$\frac{1}{s}$を含むとしましょう。
この時、$G\left(s\right)$を一般的な表現で示せば、
$$G\left(s\right)=\frac{1}{s}\frac{1}{s+\alpha_1}\frac{1}{s+\alpha_2}・・・\frac{1}{s+\alpha_n}\tag{6}$$
となりますが、$s→0$とすれば、
$$\begin{align}
\lim_{s→0}G\left(s\right)&=\frac{1}{0}\frac{1}{0+\alpha_1}\frac{1}{0+\alpha_2}・・・\frac{1}{0+\alpha_n}\\
&=\infty\tag{7}
\end{align}$$
となることがわかります。
逆に積分要素がなければ、
$$G\left(s\right)=\frac{1}{s+\alpha_1}\frac{1}{s+\alpha_2}・・・\frac{1}{s+\alpha_n}\tag{8}$$
となるので、$s→0$とすれば、
$$\begin{align}
\lim_{s→0} G\left(s\right)&=\frac{1}{0+\alpha_1}\frac{1}{0+\alpha_2}・・・\frac{1}{0+\alpha_n}\\
&=\frac{1}{\alpha_1\alpha_2・・・\alpha_n}\tag{9}
\end{align}$$
となって、$\infty$になりません。
以上より、$G(s)$に積分要素$\frac{1}{s}$があれば、定常偏差は0になることは緒管的にイメージできるかと思います。
具体的な計算例
定常偏差が0になる例
例えば、図3のフィードバック制御系を考えてみます。
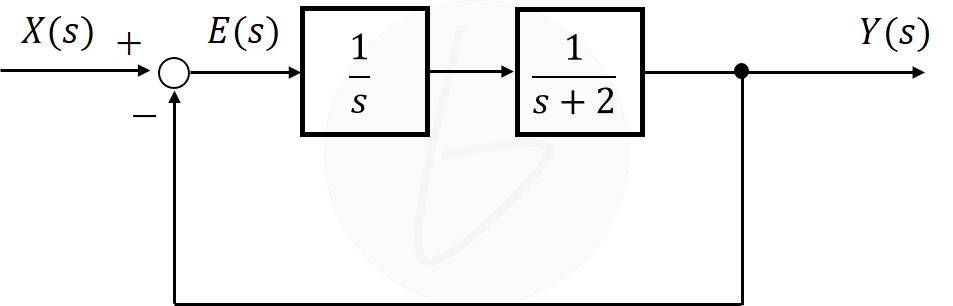
図3 フィードバック制御系の定常偏差の例①
図3のフィードバック制御系について、伝達関数は、フィードバック制御系の伝達関数の公式から、
$$\begin{align}
G\left(s\right)&=\frac{\frac{1}{s}\frac{1}{s+2}}{1+\frac{1}{s}\frac{1}{s+2}}\\
&=\frac{1}{s\left(s+2\right)+1}\\
&=\frac{1}{s^2+2s+1}\tag{10}
\end{align}$$
となります。
このフィードバック制御系に、目標値$x\left(t\right)$として、
$$x\left(t\right)=u\left(t\right)\tag{11}$$
と、単位ステップ関数を与えた場合を考えます。
この時の出力$Y\left(s\right)$は、
$$Y\left(s\right)=\frac{1}{s^2+2s+1}\frac{1}{s}\tag{12}$$
となります。
偏差$E\left(s\right)$は、
$$\begin{align}
E\left(s\right)&=X\left(s\right)-Y\left(s\right)\\
&=\frac{1}{s}-\frac{1}{s^2+2s+1}\frac{1}{s}\\
&=\frac{1}{s}\left(1-\frac{1}{s^2+2s+1}\right)\tag{13}
\end{align}$$
となり、定常偏差は、
$$\begin{align}
e\left(\infty\right)&=\lim_{s→0}sE\left(s\right)\\
&=\lim_{s→0}s\left\{\frac{1}{s}\left(1-\frac{1}{s^2+2s+1}\right)\right\}\\
&=0\tag{14}
\end{align}$$
となります。
これは、このフィードバック制御系において、目標値をステップ上に変化させたとき、言い換えれば、目標値を$x\left(t\right)=u\left(t\right)$に従って、$t=0$のタイミングで$1$に変更したとき、十分長い時間が経過すれば、偏差$e\left(t\right)=0$となり、出力は目標値と完全に一致することを示しています。
試しに、逆ラプラス変換して時間空間$t$における応答波形も確認しておきます。
$$\begin{align}
Y\left(s\right)&=\frac{1}{s^2+2s+1}\frac{1}{s}\\
&=\frac{1}{s}-\frac{1}{\left(s+1\right)^2}-\frac{1}{s+1}
\end{align}$$
逆ラプラス変換すれば、
$$\begin{align}
y\left(t\right)=1-te^{-t}-e^{-t}
\end{align}$$
となって、グラフで示すと図4の応答波形になります。
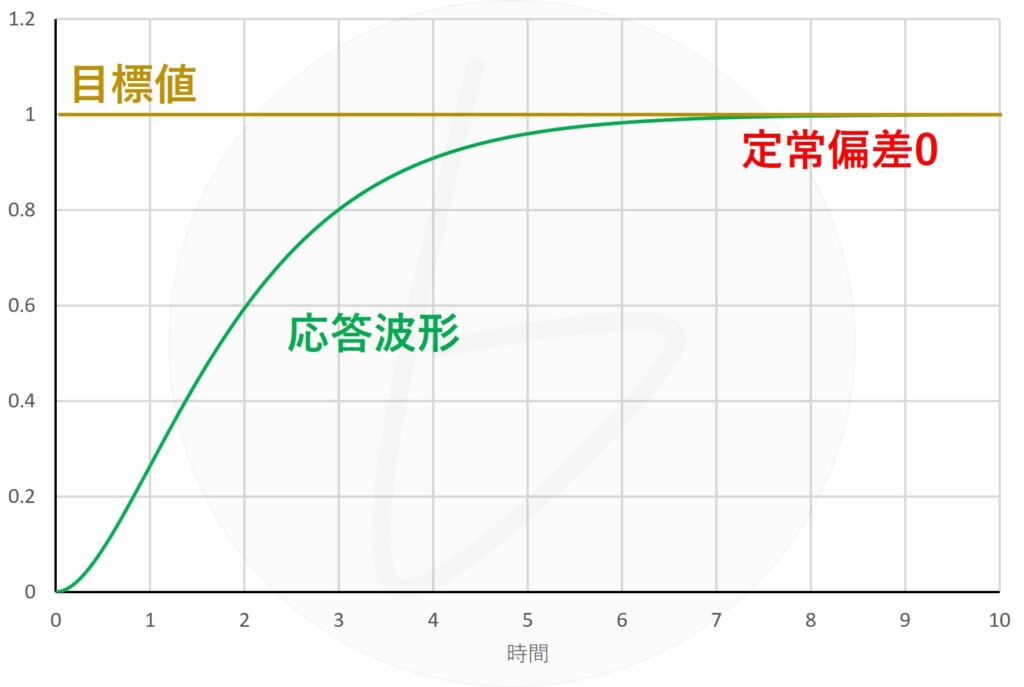
図4 定常偏差が0になるときの応答波形
なお、$te^{-t}$の項について、$t→\infty$の時、$te^{-t}$の$t$が$\infty$になり発散するように見えますが、$e^{-t}$が$0$に収束する方が速いので、安定性には影響しません。
$G\left(s\right)$について、特性方程式が、
$$s^2+2s+1=0$$
$$\left(s+1\right)^2=0$$
となって、極は$s=-1$(重解)であり実部が負になることからも明らかです。
定常偏差が定数で残る例
定常偏差は、すべてのフィードバック制御系で0になるとは限らず、ある定数が残る場合もあります。
例えば、図5のフィードバック制御系を考えてみます。
図5のフィードバック制御系は、図3のフィードバック制御系と比較して、積分の伝達関数\frac{1}{s}が取り除かれた制御系になっています。
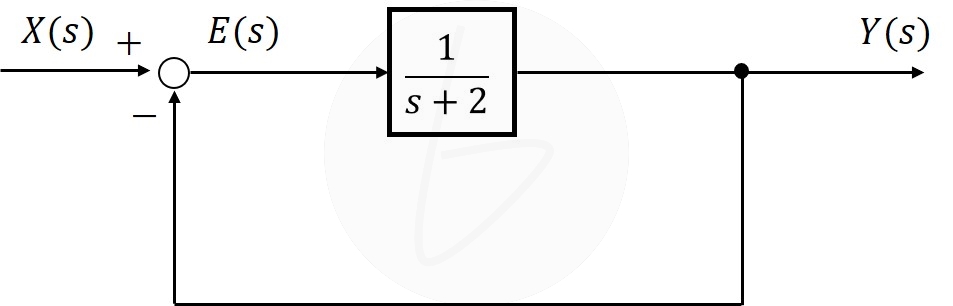
図5 フィードバック制御系の定常偏差の例②
図5のフィードバック制御系について、伝達関数は、フィードバック制御系の伝達関数の公式から、
$$G\left(s\right)=\frac{\frac{1}{s+2}}{1+\frac{1}{s+2}}=\frac{1}{s+3}\tag{14}$$
となります。
目標値としては、同様に単位ステップ関数を与えたとすれば、出力は、
$$Y\left(s\right)=\frac{1}{s+3}\frac{1}{s}\tag{15}$$
となります。
ここで、偏差$E\left(s\right)$は、
$$\begin{align}
E\left(s\right)&=X\left(s\right)-Y\left(s\right)\\
&=\frac{1}{s}-\frac{1}{s+3}\frac{1}{s}\\
&=\frac{1}{s}\left(1-\frac{1}{s+3}\right)\tag{16}
\end{align}$$
となります。
最終値の定理より、定常偏差は、
$$\begin{align}
e\left(\infty\right)&=\lim_{s→0}sE\left(s\right)\\
&=\lim_{s→0}s\left\{\frac{1}{s}-\frac{1}{s+3}\frac{1}{s}\right\}\\
&=1-\frac{1}{0+3}\\
&=\frac{2}{3}\tag{17}
\end{align}$$
となります。
今回の例のように、もしも定常偏差にある定数が残れば、目標値と実際の出力は無限に長い時間を経過しても常に定数分だけ差が出ることになり、目標値と出力が完全に一致することはありません。
定常偏差が残る場合も、試しに逆ラプラス変換して、時間空間$t$の応答波形でも確認しておきます。
$$\begin{align}
Y\left(s\right)&=\frac{1}{s+3}\frac{1}{s}\\
&=\frac{1}{3}\frac{1}{s}-\frac{1}{3}\frac{1}{s+3}
\end{align}$$
$$y\left(t\right)=\frac{1}{3}-\frac{1}{3}e^{-3t}$$
応答波形は図6の通りになり、十分長い時間が経過しても、目標値$x\left(t\right)$と出力$y\left(t\right)$の間には、$\frac{2}{3}$の定常偏差が残ることになります。
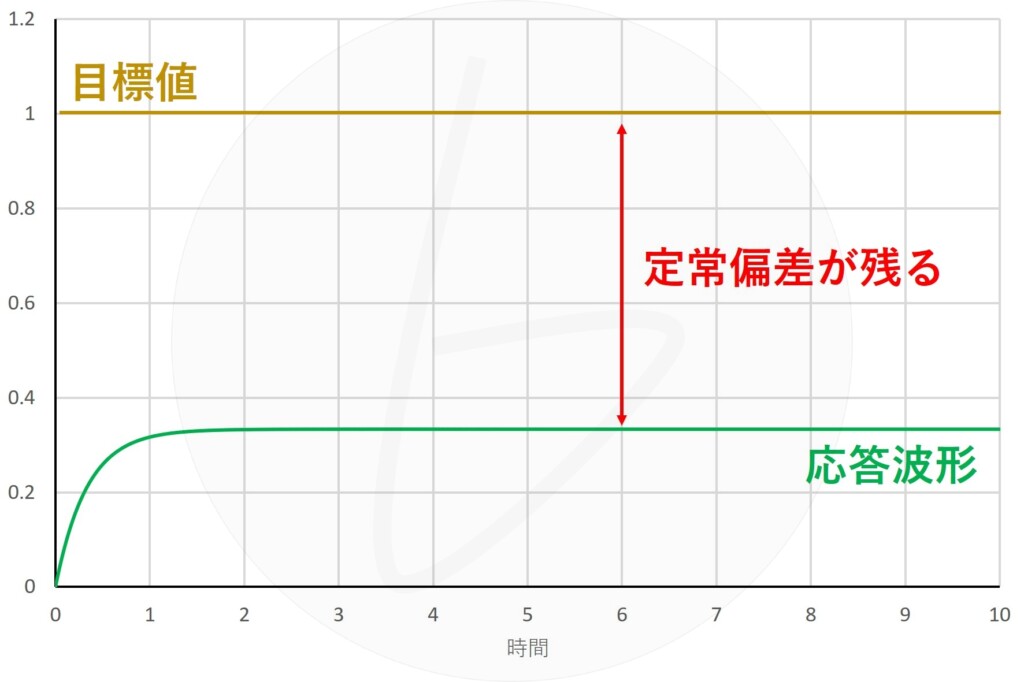
図6 定常偏差が残るときの応答波形
まとめ
ここまで、フィードバック制御系の定常偏差の計算方法と、定常偏差を積分要素を追加することで0にする方法を説明してきました。
制御系を構築していて、定常偏差を0にしたい場合には、前向き伝達関数に積分要素を追加することを検討してください。
以上、フィードバック制御系の定常偏差と、積分要素を使って定常偏差を0にする方法について、参考になれば幸いです。
●紙の本:3,850円(税込)
電験2種 二次試験 機械・制御で出題される自動制御を完答することを目的に作成した参考書。
機械・制御において、自動制御で満点を狙い、確実に合格したい場合には、この参考書がおすすめです。