この記事では、令和3年度 電験2種 二次試験 電力・管理 問4の過去問解説をしています。
問題の内容としては、三相3線式高圧配電線の末端の需要家が分散型電源を接続し、線路に逆潮流が生じている状況において、需要家の電圧がどれだけ上昇するかを計算する問題です。
この問題では、小問(1)の逆潮流のベクトル図が若干ややこしいです。
小問(2)は、単に三平方の定理で解けるので、サービス問題となりますが、数字があまりにも大きく、$\mathrm{kV}$単位で計算しないと電卓がオーバーフローするので注意しましょう。
令和3年度 電験2種 二次試験 電力・管理 問4
分散形電源の系統連系に関して、次の問に答えよ。
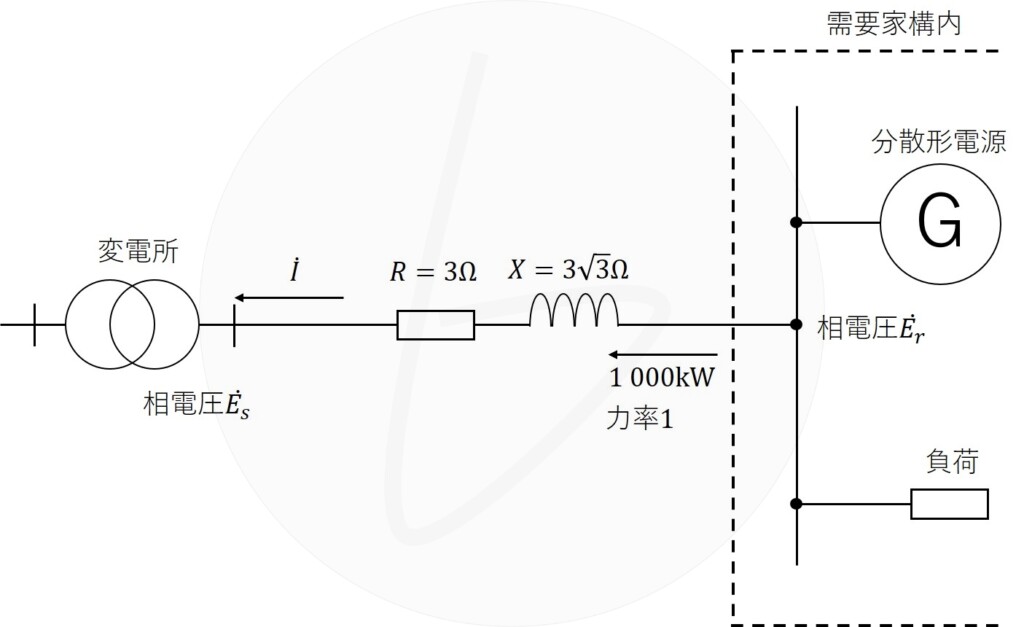
図に示す$6.6{\rm kV}$三相3線式高圧配電線の末端に、分散形電源を有する需要家が連系されている。
(1)需要家から配電線へ逆潮流(力率$1$)がある場合の、需要家端の相電圧(1線と中性点間の電圧)$\dot{E_r}$と変電所の相電圧$\dot{E_s}$の関係を示すベクトル図及び関係式を$\dot{E_s}$、$\dot{E_r}$、$\dot{I}$、$R$、$X$を用いて描け。ただし、ベクトル図は$\dot{E_r}$(位相$0$)を基準とし、電流$\dot{I}$は図中の矢印の向きを正とする。
(2)小問(1)のベクトル図から需要家端の線間電圧値を求めよ。ただし、需要家端からの逆潮流は$1 000{\rm kW}$、力率は$1$(分散形電源、負荷設備ともに$1$)であり、高圧配電線は当該需要家のみの専用線とし、1線当たりの抵抗$R$及びリアクタンス$X$はそれぞれ$3{\rm Ω}$及び$3\sqrt{3}{\rm Ω}$、変電所端の線間電圧は$6.6{\rm kV}$で一定とする。
解答・解説
小問(1)
配電線に逆潮流が生じており、
$$\dot{E_r}=\dot{E_s}+\left(R+jX\right)I\tag{1}$$
となっている。
ベクトル図として$\dot{E_r}$を基準にする必要があるから、式(1)を変形して、
$$\dot{E_s}=\dot{E_r}-\left(R+jX\right)I\tag{2}$$
となる。
以上より、$\dot{E_r}$を基準としてベクトル図を描くと、解図1の通りになる。
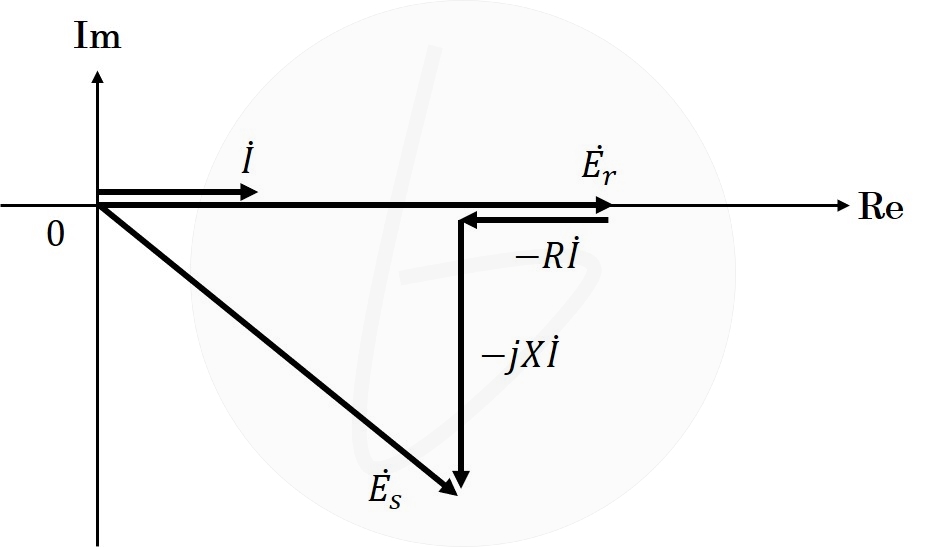
解図1
(答)解図1に示す通り。
小問(2)
分散形電源が配電線に流す電流は、逆潮流が$1 000{\rm kW}$(三相分であることに注意)、力率$1$、受電端電圧$E_r\left[{\rm kV}\right]$より、
$$I=\frac{1000}{3E_r}\tag{3}$$
これより、解図2に示す通り、$\dot{E_s}$の虚部は、
$$\begin{align}
Im\left[\dot{E_s}\right]&=XI\\
&=3\sqrt{3}×\frac{1000}{3E_r}\\
&=\sqrt{3}×\frac{1000}{E_r}\tag{4}
\end{align}$$
である。
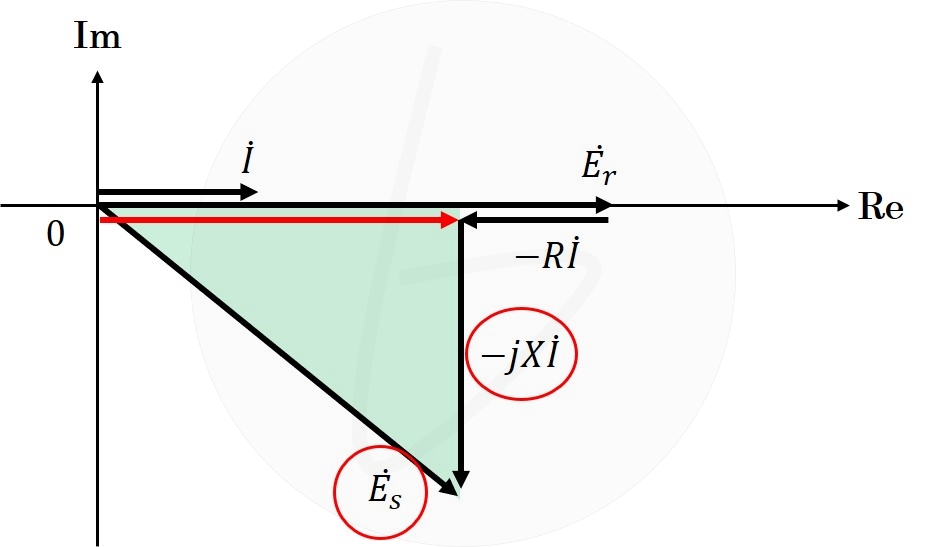
解図2
以上より、$\dot{E_s}$の実軸成分は、
$$\begin{align}
Re\left[\dot{E_s}\right]&=\sqrt{E_s^2-\left(XI\right)^2}\\
&=\sqrt{\left(\frac{6.6}{\sqrt3}\right)^2-\left(\sqrt3×\frac{1000}{E_r}×\frac{1}{1000}\right)^2}\\
&=\sqrt{\left(\frac{6.6}{\sqrt{3}}\right)^2-\left(\sqrt{3}×\frac{1}{E_r}\right)^2}\left[{\rm kV}\right]\tag{5}
\end{align}$$
となる。
※式(5)では計算単位を[kV]にしている点に注意。[V]で計算すると電卓がオーバーフローします。
解図3に示す通り、
$$E_r=Re\left[\dot{E_s}\right]+RI\tag{6}$$
であるから、
$$\begin{align}
E_r&=\sqrt{\left(\frac{6.6}{\sqrt3}\right)^2-\left(\sqrt3×\frac{1}{E_r}\right)^2}+3×\frac{1000}{3E_r}×\frac{1}{1000}\\
&=\sqrt{\left(\frac{6.6}{\sqrt{3}}\right)^2-\left(\sqrt{3}×\frac{1}{E_r}\right)^2}+\frac{1}{E_r}\tag{7}
\end{align}$$
これを解くと、
$$E_r^4-16.52E_r^2+4=0\tag{8}$$
となる。
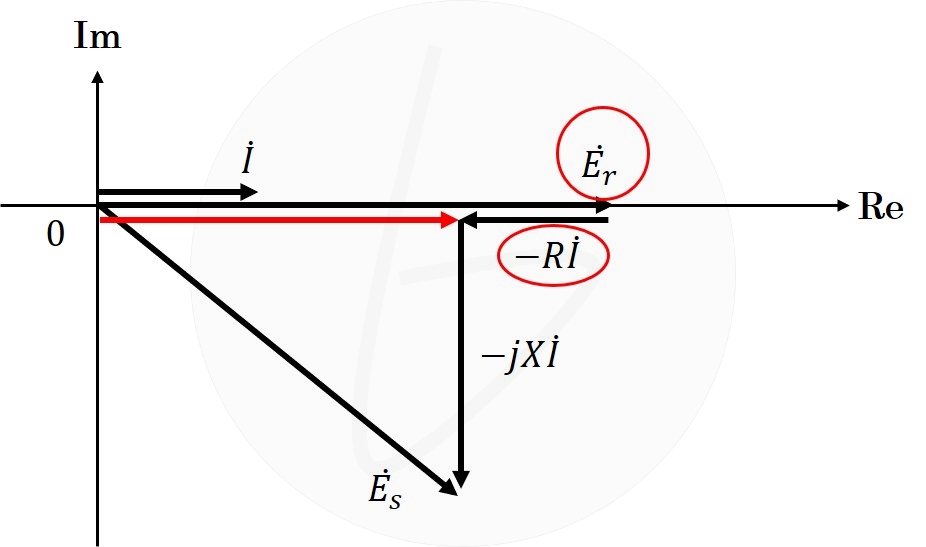
解図3
解の公式より、
$$\begin{align}
E_r^2&=\frac{16.52±\sqrt{16.52^2-4×1×4}}{2×1}\\
&=\begin{cases}0.2457876245\\16.2742123755\end{cases}\tag{9}
\end{align}$$
ここで、$E_r^2=0.2457876245$は不適であるから、
$$E_r=4.03413093187\left[{\rm kV}\right]\tag{10}$$
線間電圧$V_r$にすると、
$$\begin{align}
V_r&=\sqrt{3}E_r\\
&=\sqrt{3}×4.03413093187\\
&=6.98711477399\left[{\rm kV}\right]\tag{11}
\end{align}$$
となる。
(答)$6.99\left[{\rm kV}\right]$
おすすめ参考書
Amazonで参考書を販売しています。
価格:2,490円
内容:重要公式が一目でわかる、40ページでまとめた参考書。
フルカラー印刷。
時短にもなる、電験2種 二次試験の必携参考書です。






