みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、フィードバック制御系における極配置と安定性について解説していきます!
極配置と安定性の要点
フィードバック制御系の伝達関数における分母を0にする方程式を特性方程式という。
$$1+一巡伝達関数=0$$
一巡伝達関数を一般系で示せば、
$$a_0s^{n}+a_1s^{n-1}+・・・+a_{n-1}s+a_n=0$$
になる。
この時、特性方程式の解(すなわち伝達関数の極)の実部が、
- すべて負であるとき:安定
- 正となる解が一つでも含まれる:不安定
となる。
安定な場合の応答波形は青のように収束し、不安定な場合の応答波形は赤のように発散する。
一般的に特性方程式は$s$の次数が高い多項式であり、因数分解により解を求めるのは困難。
そこで、ラウスの安定判別法やフルビッツの安定判別法を用いて、単純な計算で安定性を判別する。
極配置と安定性の直感的な理解
一般的なプロパーな伝達関数における安定性を考えていきます。
一般的に伝達関数は、
$$G\left(s\right)=\frac{b_0s^m+b_1s^{m-1}+・・・+b_{m-1}s+b_m}{a_0s^n+a_1s^{n-1}+・・・+a_{n-1}s+a_n}\tag{1}$$
※ただし、$n>m$(これをプロパーな伝達関数といいます)
です。
そして、分母=0となる方程式、
$$a_0s^n+a_1s^{n-1}+・・・+a_{n-1}s+a_n=0\tag{2}$$
を、”特性方程式”と呼びます。
さらに、特性方程式の解となるsの値を”極”といいます。
極の値は、制御系の安定性に直結しています。
例えば、
$$G\left(s\right)=\frac{1}{s-a}\tag{3}$$
の場合、極は$s-a=0$を解いて、$s=a$となります。
仮に、一般化のために$a$が複素数だったとして、
$$a=b+j\omega\tag{4}$$
とし、$G\left(s\right)$を逆ラプラス変換すると、
$$e^{at}=e^{\left(b+j\omega\right)t}=e^{bt}\left(cos\omega t+jsin\omega t\right)\tag{4}$$
となります。
さて、$e^{at}$が0に収束するための条件を考えてみると、$e^{bt}$が$t→\infty$で0になればOKです。
そのためには、$b<0$が必須条件です。
$\omega$がどんな値であっても、-1~1の範囲内で三角関数の振動が激しくなったり、ゆっくりになったりするだけで、$t→\infty$での収束には関係ありません。
一方で、$b>0$であれば$\infty$に発散します。
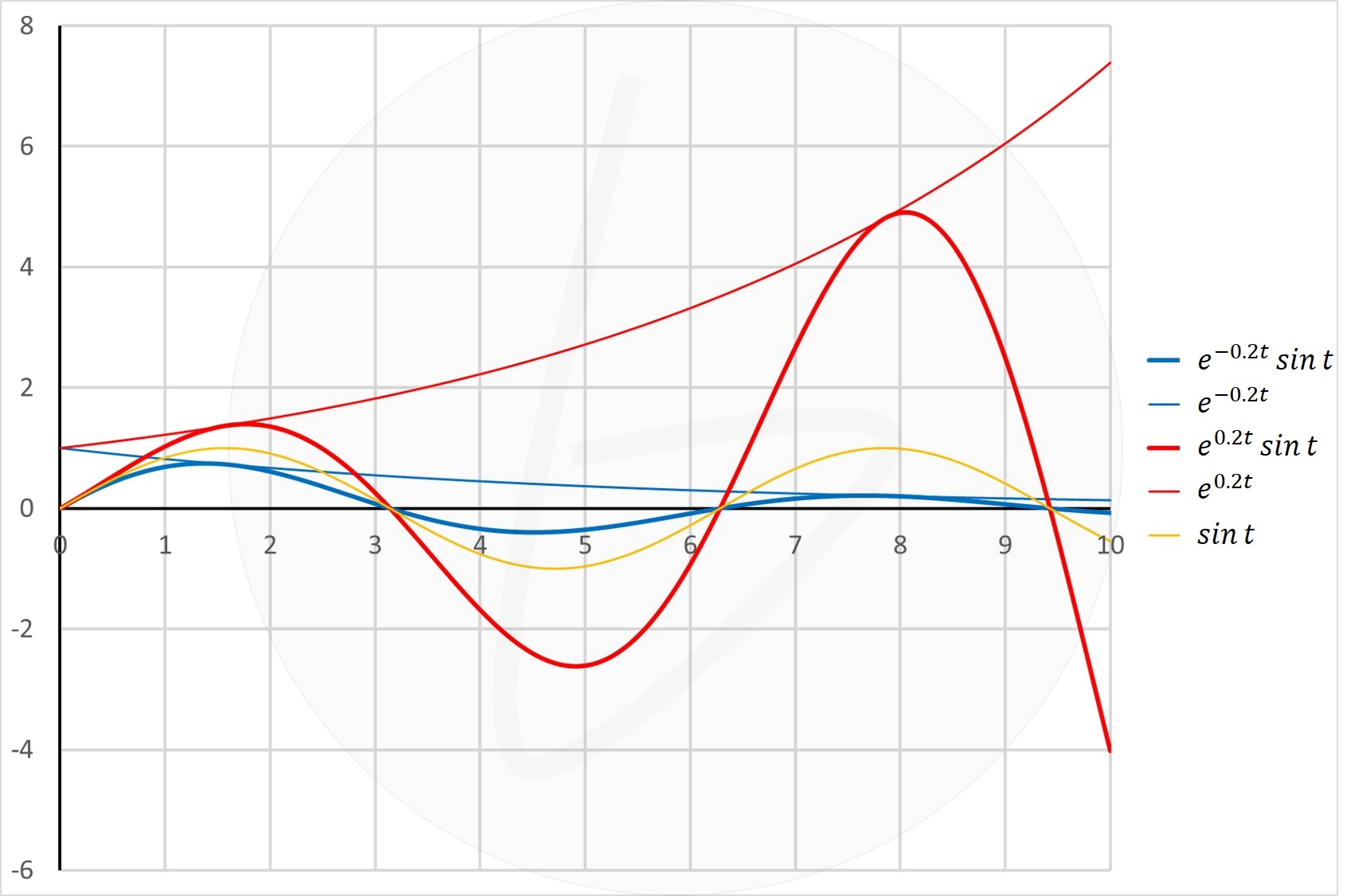
具体的な波形が図1になります。図1では、試しに、
$$\begin{cases}
b=±0.2\\
\omega=1
\end{cases}\tag{5}$$
とし、
$$\begin{cases}
e^{-0.2t}sint\\
e^{0.2t}sint
\end{cases}\tag{6}$$
の2つの関数を示しました。
$sint$は振動的な関数ですが、
青線:$b=-0.2<0$の場合、$e^{-0.2t}$が0に収束する
→それらの積である$e^{-0.2t}sint$は0に収束する安定な応答波形
赤線:$b=0.2>0$である$e^{0.2t}$が発散する
→それらの積である$e^{0.2t}sint$は、発散する不安定な応答波形
になっています。

図1 極の実部の符号と安定性の関係
極配置と安定性をより一般的に考える
さて、より一般化して考えてみます。式(1)に示すプロパーな伝達関数は、分母を因数分解して、
$$\begin{align}
G\left(s\right)&=\frac{b_0s^m+b_1s^{m-1}+・・・+b_{m-1}s+b_m}{a_0s^n+a_1s^{n-1}+・・・+a_{n-1}s+a_n}\\
&=\frac{b_0s^m+b_1s^{m-1}+・・・+b_{m-1}s+b_m}{\left(s-\alpha_0\right)\left(s-\alpha_1\right)\left(s-\alpha_2\right)・・・\left(s-\alpha_{n-1}\right)\left(s-\alpha_n\right)}\tag{7}
\end{align}$$
となります。
さらに、式(7)を部分分数分解して、
$$G\left(s\right)=\frac{A_n}{s-\alpha_0}+\frac{A_{n-1}}{s-\alpha_1}+\frac{A_{n-2}}{s-\alpha_2}+・・・+\frac{A_1}{s-\alpha_{n-1}}+\frac{A_0}{s-\alpha_n}\tag{8}$$
となります。
ここで、それぞれの項の逆ラプラス変換の結果は、
- $e^{\alpha_0t}$
- $e^{\alpha_1t}$
- $e^{\alpha_2t}$
と続き、
- $e^{\alpha_{n-1}t}$
- $e^{\alpha_nt}$
となります。
以上の検討内容より、これらの$\alpha_n$~$\alpha_0$の値について、”すべての極”の実部が負であれば安定、それ以外は不安定となります。
重要なこととして、たった一つでも不安定な極があれば、その項が発散するので、制御系は不安定になります。
例えば、次の式において、
$$A_0e^{\alpha_0t}+A_1e^{\alpha_1t}+A_2e^{\alpha_2t}+・・・+A_{n-1}e^{\alpha_{n-1}t}+A_ne^{\alpha_nt}$$
の時、例えば$\alpha_0$の実部が正であれば、$A_0e^{\alpha_0t}$は発散します。
この時、ほかの項がどれだけ0に収束しようとも、$A_0e^{\alpha_0t}$の発散を止めることはできません。
まとめ
ここまで、フィードバック制御系における極配置と安定性について解説してきました。
極の実部が負であれば安定です。
一方、ただ一つだけでも極の実部がになる場合にあば、無条件に不安定です。
これらは、
$$\mathcal{L}\left[e^{at}\right]=\frac{1}{s-a}$$
からも明らかです。
なお、極を求める時には伝達関数の分母、あるいは特性方程式を因数分解する必要があります。
一般的に特性方程式は多次元の方程式になってしまうので、手計算で極を求めるのは困難です。
そこで、ラウスの安定判別法や、フルビッツの安定判別法があり、手軽に安定性判別ができるようになっています。
こちらの記事も併せてご覧ください。
以上、フィードバック制御系の極配置と、安定性について参考になれば幸いです。
●紙の本:3,850円(税込)
電験2種 二次試験 機械・制御で出題される自動制御を完答することを目的に作成した参考書。
機械・制御において、自動制御で満点を狙い、確実に合格したい場合には、この参考書がおすすめです。





