二次遅れ系のインパルス応答の応答波形と具体的な計算方法

みなさん、こんにちは！

ブリュの公式ブログ.org（for Academic Style）にお越しいただきまして、ありがとうございます！

今回は、自動制御の二次遅れ系のインパルス応答について、

• 実数解
• 重解
• 虚数解

を持つ場合の応答波形について、場合分けをしながら説明していきます。

なお、二次遅れ系の極と応答波形のイメージを理解するには、二次遅れ系の極と応答波形の概要を参考にして下さい。

極とラプラス変換の関係から、$sin$, $cos$を含むか否かといった直感的イメージが理解できます。

二次遅れ系のインパルス応答の要点

二次遅れ系にインパルス応答が入力されると、瞬間的に値が振れますが、のちに0位置に戻ります。

この時、極の値によって、

• 橙：$\xi<1$（不足減衰）
• 緑：$\xi=1$（臨界減衰）
• 赤：$\xi>1$（過減衰）

といった場合分けが可能であり、図1のような応答波形が得られます。

緑で示す$\xi=1$の時は臨界減衰で位置に最も早く戻ってきますが、$\xi$が大きくなると逆に0位置になかなか戻ってこない過減衰になり、$\xi$が小さくなると今度は0位置近傍での振動が生じる不足減衰になります。

これらの応答波形は極の値によって支配されているので、場合分けして考えていきます。

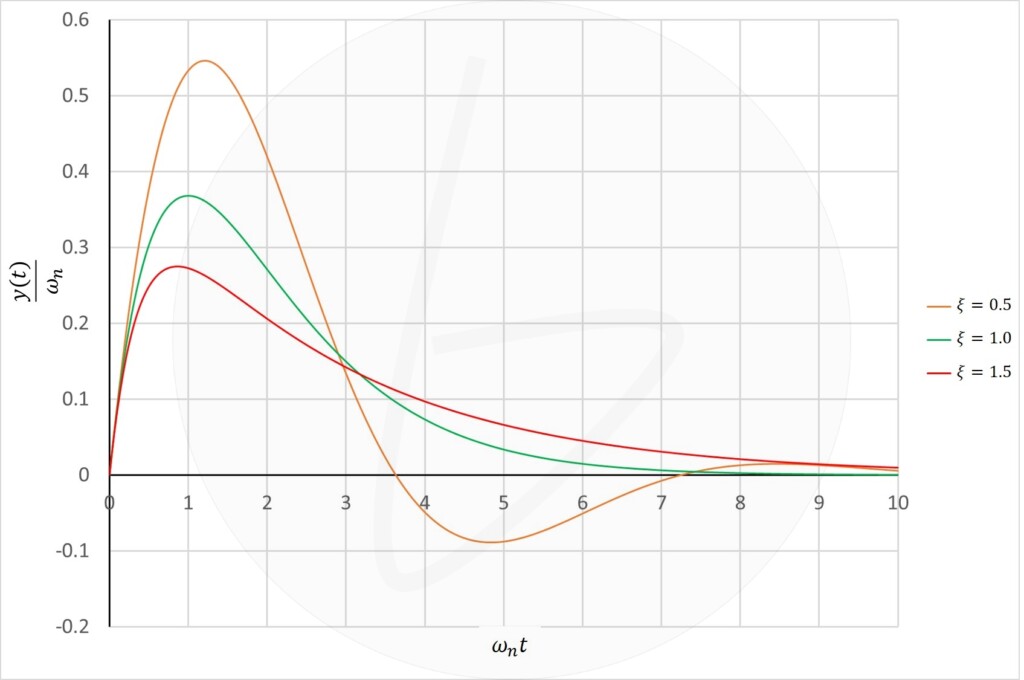
図　二次遅れ系のインパルス応答波形（不足減衰, 臨界減衰, 過減衰）

二次遅れ系のインパルス応答の場合分けと具体的な計算手法

二次遅れ系のインパルス応答を見ていきます。

インパルス応答、すなわちデルタ関数を入力した状況です。

出力は、$Y\left(s\right)$は、

$$Y\left(s\right)=G\left(s\right)X\left(s\right)\tag{1}$$

で示され、デルタ関数$x\left(t\right)=\delta\left(t\right)$のラプラス変換は$X\left(s\right)=1$であることから、そのまま伝達関数が出力され、

$$Y\left(s\right)=G\left(s\right)・1=G\left(s\right)=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}\tag{2}$$

となります。

言い換えれば、伝達関数そのものを時間領域に逆ラプラス変換したものが、インパルス応答です。

分母についての部分分数分解を考えるために、分母=0、すなわち、

$$s^2+2\xi\omega_ns+\omega_n^2=0\tag{3}$$

を解くと、解の公式より、

$$s=\frac{-2\xi\omega_n±\sqrt{4\xi^2\omega_n^2-4\omega_n^2}}{2}=\omega_n\left(-\xi±\sqrt{\xi^2-1}\right)\tag{4}$$

となります。

解の第2項である$\sqrt{\xi^2-1}$は、$\xi$の大きさによって、実数、0、虚数の3パターンがあります。

以上より、二次遅れ要素のインパルス応答では、

• $\xi>1$（実数解）
• $\xi=1$（重解）
• $\xi<1$（虚数解）

にわけて検討を行う必要があります。

①$\xi>1$の時（実数解の時）：過減衰

実数解の時、三角関数の項を含まないので、振動しない解になります。

$$\begin{align}
Y\left(s\right)&=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}\\
&=\frac{\omega_n^2}{\left(s-\omega_n\left(-\xi+\sqrt{\xi^2-1}\right)\right)\left(s-\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)\right)}\\
&=\frac{A}{s-ω_n\left(-\xi+\sqrt{\xi^2-1}\right)}+\frac{B}{s-\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)}\tag{5}
\end{align}$$

$$\begin{align}
A&=\lim_{s→\omega_n\left(-\xi+\sqrt{\xi^2-1}\right)} \frac{\omega_n^2}{s-\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)}\\
&=\frac{\omega_n}{2\sqrt{\xi^2-1}}\tag{6}
\end{align}$$

$$\begin{align}
B&=\lim_{s→\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)} \frac{\omega_n^2}{s-\omega_n\left(-\xi+\sqrt{\xi^2-1}\right)}\\
&=-\frac{\omega_n}{2\sqrt{\xi^2-1}}\tag{7}
\end{align}$$

以上より、

$$Y\left(s\right)=\frac{\omega_n}{2\sqrt{\xi^2-1}}\left(\frac{1}{s-\omega_n\left(-\xi+\sqrt{\xi^2-1}\right)}-\frac{1}{s-\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)}\right)\tag{8}$$

逆ラプラス変換すると、

$$\begin{align}
y\left(t\right)&=\frac{\omega_n}{2\sqrt{\xi^2-1}}\left(e^{\omega_n\left(-\xi+\sqrt{\xi^2-1}\right)t}-e^{\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)t}\right)
\\
&=\frac{\omega_n}{2\sqrt{\xi^2-1}}e^{-\xi\omega_nt}\left(e^{\omega_n\sqrt{\xi^2-1}t}-e^{-\omega_n\sqrt{\xi^2-1}t}\right)\tag{9}
\end{align}$$

双曲線関数を用いて表現すると、

$$sinh x=\frac{e^x-e^{-x}}{2}\tag{10}$$

より、

$$Y\left(t\right)=\frac{\omega_n}{\sqrt{\xi^2-1}}e^{-\xi\omega_nt}sinh\left(\omega_n\sqrt{\xi^2-1}t\right)\tag{11}$$

となります。

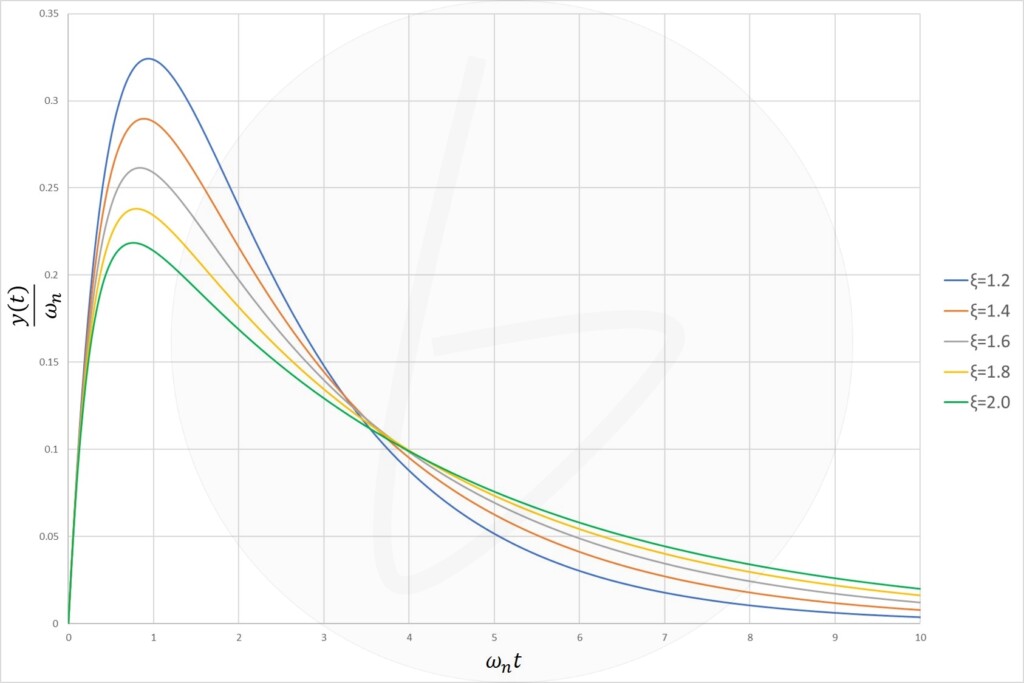
図1　二次遅れ要素のインパルス応答（$\xi>1$）

② $\xi=1$の時（重解の時）：臨界減衰

$\xi=1$で重解になる場合、式(4)で示されるよう$\sqrt{}$内部が$0$となるため、重解となります。

よって分母を2乗でくくることができます。

$$\begin{align}
Y\left(s\right)&=\frac{\omega_n^2}{s^2+2\omega_ns+\omega_n^2}\\
&=\frac{\omega_n^2}{\left(s+\omega_n\right)^2}\tag{12}
\end{align}$$

式(12)を逆ラプラス変換すると、式(13)になります。

$$y\left(t\right)=\omega_n^2te^{-\omega_nt}\tag{13}$$

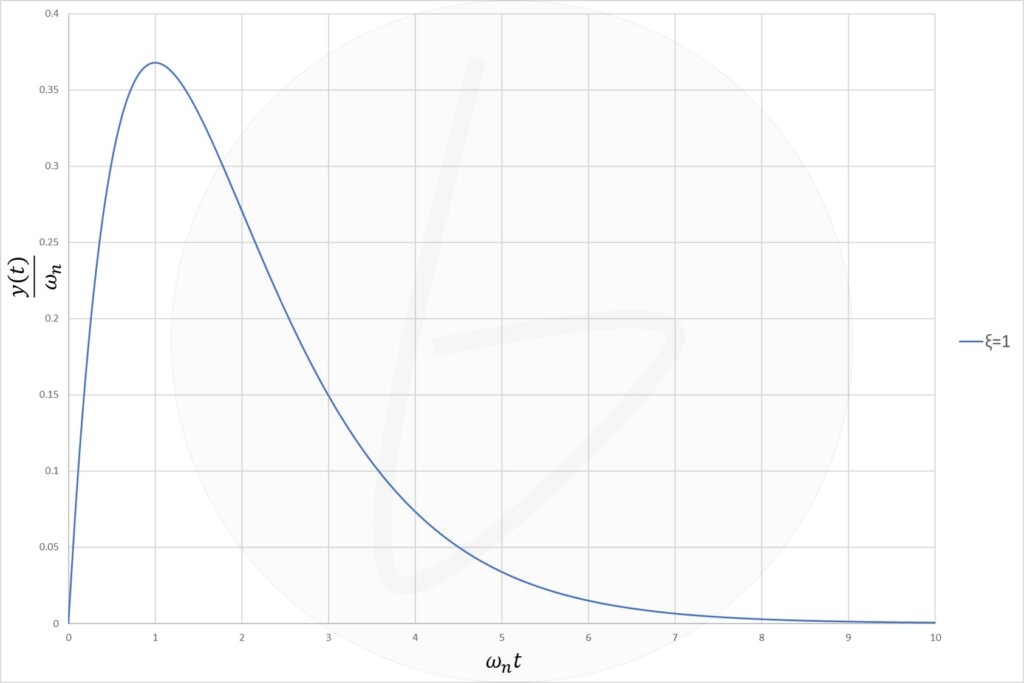
図2　二次遅れ要素のインパルス応答（$\xi=1$）

③ $\xi<1$の時（虚数解の時）：不足減衰

虚数解がある場合、解は三角関数を含みます。

そのため、振動的な応答になります。

$$\begin{align}
Y\left(s\right)&=\frac{\omega_n^2}{s^2+2\xi\omega_ns+\omega_n^2}\\
&=\frac{\omega_n^2}{\left(s-\omega_n\left(-\xi+\sqrt{\xi^2-1}\right)\right)\left(s-\omega_n\left(-\xi-\sqrt{\xi^2-1}\right)\right)}\\
&=\frac{\omega_n^2}{\left(s-\omega_n\left(-\xi+j\sqrt{1-\xi^2}\right)\right)\left(s-\omega_n\left(-\xi-j\sqrt{1-\xi^2}\right)\right)}\\
&=\frac{A}{s-\omega_n\left(-\xi+j\sqrt{1-\xi^2}\right)}+\frac{B}{s-\omega_n\left(-\xi-j\sqrt{1-\xi^2}\right)}\tag{14}
\end{align}$$

$$\begin{align}
A&=\lim_{s→\omega_n\left(-\xi+j\sqrt{1-\xi^2}\right)}\frac{\omega_n^2}{s-\omega_n\left(-\xi-j\sqrt{1-\xi^2}\right)}\\
&=\frac{\omega_n}{2j\sqrt{1-\xi^2}}\tag{15}
\end{align}$$

$$\begin{align}
B&=\lim_{s→\omega_n\left(-\xi-j\sqrt{1-\xi^2}\right)}\frac{\omega_n^2}{s-\omega_n\left(-\xi+j\sqrt{1-\xi^2}\right)}\\
&=-\frac{\omega_n}{2j\sqrt{1-\xi^2}}\tag{16}
\end{align}$$

$$\begin{align}
Y\left(s\right)&=\frac{\omega_n}{2j\sqrt{1-\xi^2}}\left(\frac{1}{s-\omega_n\left(-\xi+j\sqrt{1-\xi^2}\right)}-\frac{1}{s-\omega_n\left(-\xi-j\sqrt{1-\xi^2}\right)}\right)\\
&=\frac{\omega_n}{2j\sqrt{1-\xi^2}}\left(e^{\omega_n\left(-\xi+j\sqrt{1-\xi^2}\right)}-e^{\omega_n\left(-\xi-j\sqrt{1-\xi^2}\right)}\right)\tag{17}
\end{align}$$

ここで、オイラーの公式より、

$$\begin{align}
Y\left(s\right)&=\frac{\omega_n}{2j\sqrt{1-\xi^2}}\\
&e^{-\omega_n\xi t}\left(cos\sqrt{1-\xi^2}\omega_nt+jsin\sqrt{1-\xi^2}\omega_nt-cos\sqrt{1-\xi^2}\omega_nt+jsin\sqrt{1-\xi^2}\omega_nt\right)\\
&=\frac{\omega_n}{\sqrt{1-\xi^2}}e^{-\omega_n\xi t}sin\sqrt{1-\xi^2}\omega_nt\tag{18}
\end{align}$$

となります。

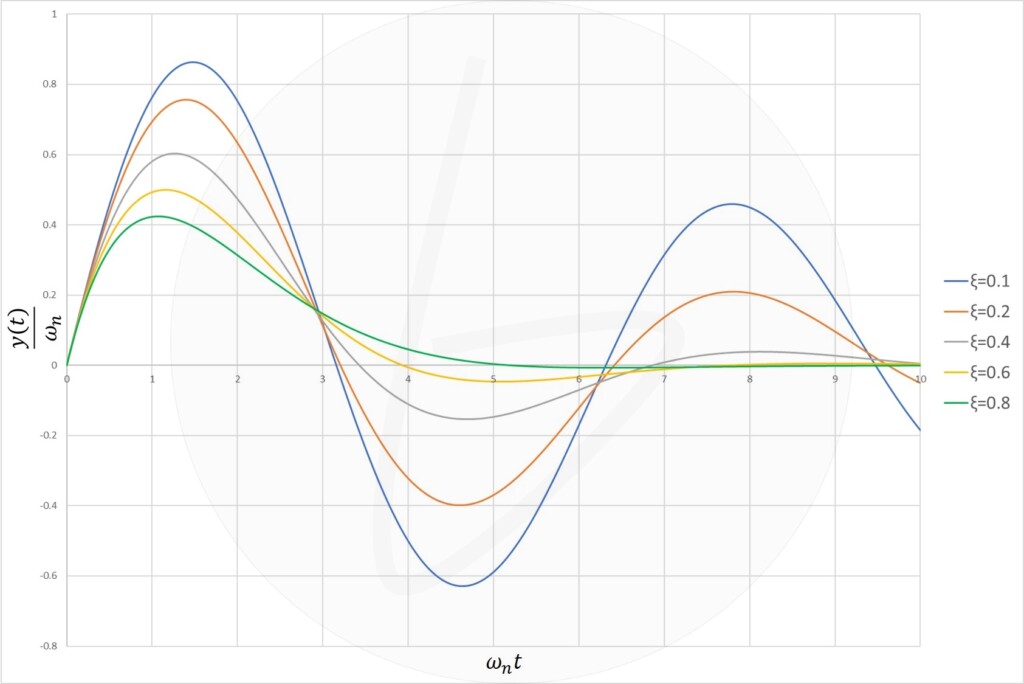
図3　二次遅れ要素のインパルス応答（$\xi<1$）

まとめ

ここまで、二次遅れ系のインパルス応答の応答波形の場合分けと計算方法について説明してきました。

図4　二次遅れ系のインパルス応答波形のまとめ

要点として、

• 極の値と逆ラプラス変換の関係から、虚数解となれば0位置近傍での振動が生じること
• $\xi$の値が大きすぎると0位置に戻るのに時間がかかる

という2点を抑えておけばいいでしょう。

以上、二次遅れ系のインパルス応答について、参考になれば幸いです。

→古典制御の記事一覧

▼書籍版もあります♪▼