みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、変圧器や電力系統の計算でよく登場する、単位法について紹介します。
単位法の単位[p.u.]なんて見ると、、、
はい・・・!?
となると思います。
私も当初はそうでした。
仕方ないと思います。
単位法を理解しようとするから難しいんです。
理解よりも先に概念を知れば、あとから理解はついてきます。。
だからこそ、皆さんに単位法の概念を知ってもらえることを狙って、この記事を作成しました。
▼おすすめ記事▼

単位法とパーセントインピーダンスの理解の仕方
定義から読み解く単位法
単位法の定義(決まり事)として、単位法の回路においてのすべての共通事項は、
- 基準容量:$S_{BASE}$[VA]
だけです。
基準容量が異なる値は、基準容量にそろうように換算します。
そして、回路各部にはそれぞれ、
- 基準電圧:$V_{BASE}$[V]
が決まっています。
そうすると、回路各部の基準電流$I_{BASE}$[A]と基準インピーダンス$Z_[BASE]$[Ω]が自然に決まりますよね。
例えば単相交流の場合、
- 基準電流:$I_{BASE}=\frac{S_{BASE}}{V_{BASE}}$
- 基準インピーダンス:$Z_{BASE}=\frac{V_{BASE}}{I_{BASE}}=\frac{{V_{BASE}}^2}{S_{BASE}}$
そして、これらに対して実際の値である、$S$[VA]、$V$[V]、$I$[A]、$Z$[Ω]の比率を表すものが、単位法です。
具体的には、
- $S$[p.u.]=$\frac{S}{S_{BASE}}$
- $V$[p.u.]=$\frac{V}{V_{BASE}}$
- $I$[p.u.]=$\frac{I}{I_{BASE}}$
- $Z$[p.u.]=$\frac{Z}{Z_{BASE}}$
そして、特にインピーダンスについて、100%換算したものがパーセントインピーダンスであり、
- $\%Z[\%]=Z[p.u.]×100=\frac{Z}{Z_{BASE}}×100$
となります。
考えてみれば単純ですよね。
パーセントインピーダンスが与えられたら、問題文の基準インピーダンスに対して何%なのかがわかっているのですから、逆算できます。
例題を考えてみる
例で考えたほうがわかりやすいでしょう。
単相変圧器において、
- 定格容量:10[kVA]
- 1次側定格電圧:1000[V]
- 2次側定格電圧:100[V]
- パーセントインピーダンス:5[%](定格容量基準)
の時、1次側、2次側換算のインピーダンス値を、単位[Ω]で求めてください。
この問題で、回路上ですべて共通なのは、定格容量10[kVA]のみです。
では答えです。
■1次側換算の場合
$$Z_{BASE}=\frac{S_{BASE}}{{V_{BASE}}^2}$$
より、
$$Z_{BASE}=\frac{10000}{1000^2}=0.01$$
よって、
$$%Z=\frac{Z_1}{Z_{BASE}}×100$$
$$5=\frac{Z_1}{0.01}×100$$
$$Z_1=0.0005[Ω]$$
■2次側換算の場合
同様に、
$$Z_{BASE}=\frac{10000}{100^2}=1$$
$$5=\frac{Z_2}{1}×100$$
$$Z_2=0.05[Ω]$$
■変圧比との関係
この変圧器は、変圧比が$\frac{1000}{100}=10$です。
変圧器の等価回路において、1次側のインピーダンスを2次側に変換する場合、$変圧比^2$倍の換算、今回の場合$10^2$倍の換算が必要です。
ここでつまずいた方は、変圧器の等価回路の説明をご覧ください。
よく見てみると・・・
- $Z_1=0.0005$[Ω]
- $Z_2=0.05$[Ω]
ちょうど、$100^2=10000$倍の関係になっていますよね。
これが単位法の効果です。
変圧比を意識せずに、電圧の異なる電気回路を、あたかも一つの線で繋がったかのような電気回路に変換できるのです。
単位法と変圧器、および電力系統の関係
単位法で見る変圧器
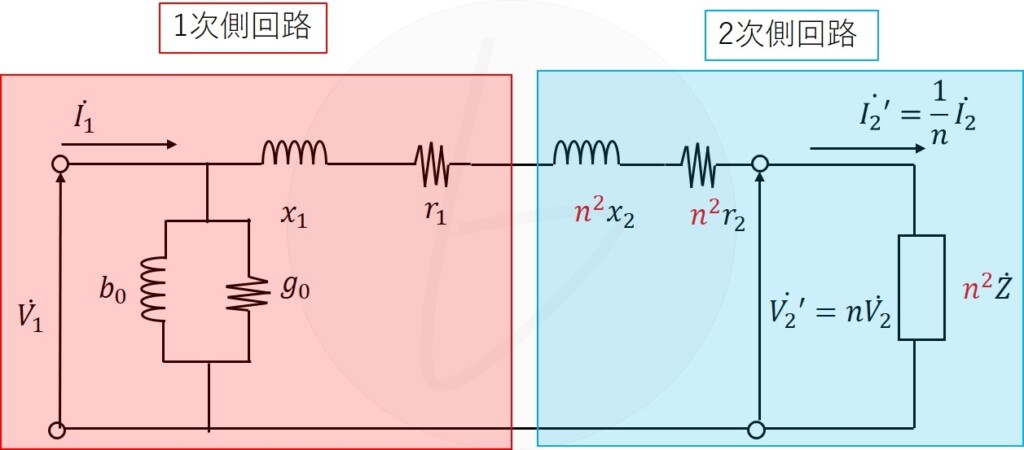
変圧器の等価回路を考えるには、変圧比に応じたインピーダンス値の変換が必要でした。
■1次側換算
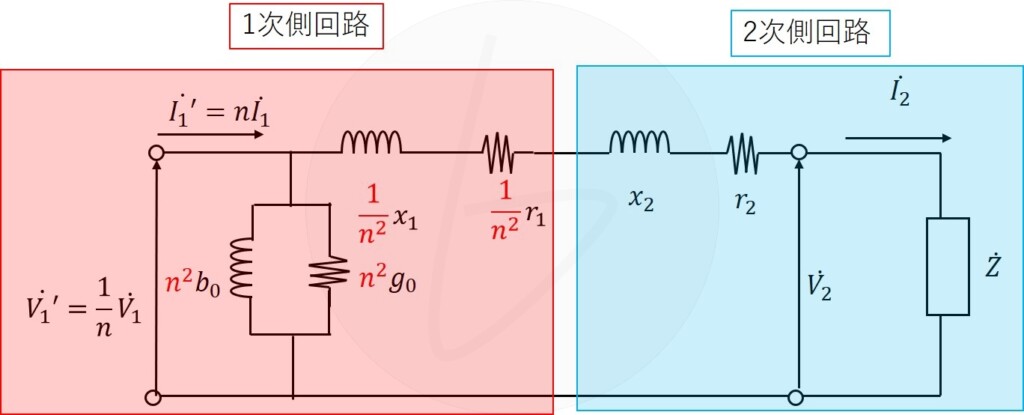
■2次側換算
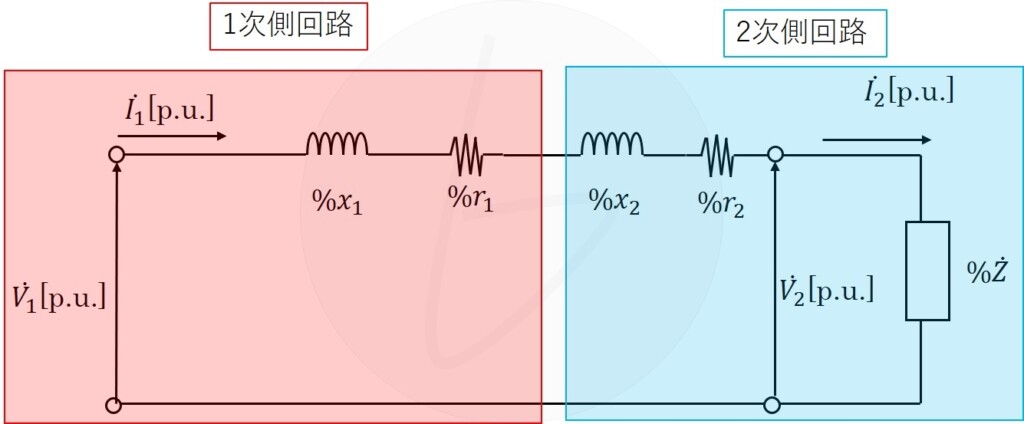
しかし、単位法では、基準容量その割合を示します。
そして、計算対象の基準電圧を1p.u.とおけば、各部の値が計算できることになります。
電力系統はは変圧器の集合体である
単位法が効いてくるのは、電力系統の計算時です。
電力系統は、変圧器の集合体であることはご存じでしょう。
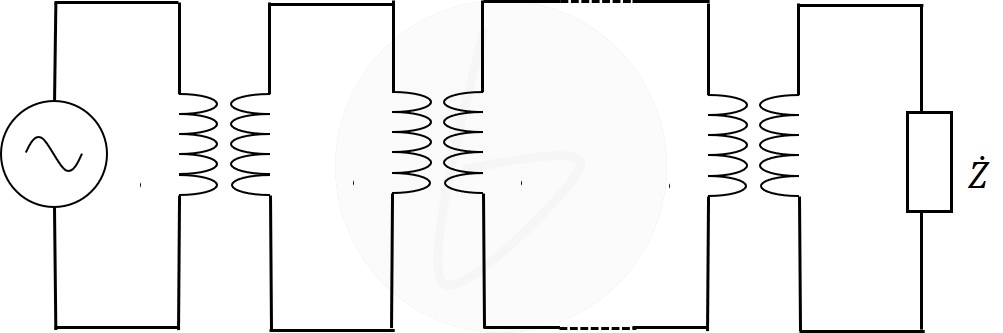
その時に、Ω値での変圧器の等価回路では、何を基準に何倍するのかを考える必要があり、計算が複雑化します。
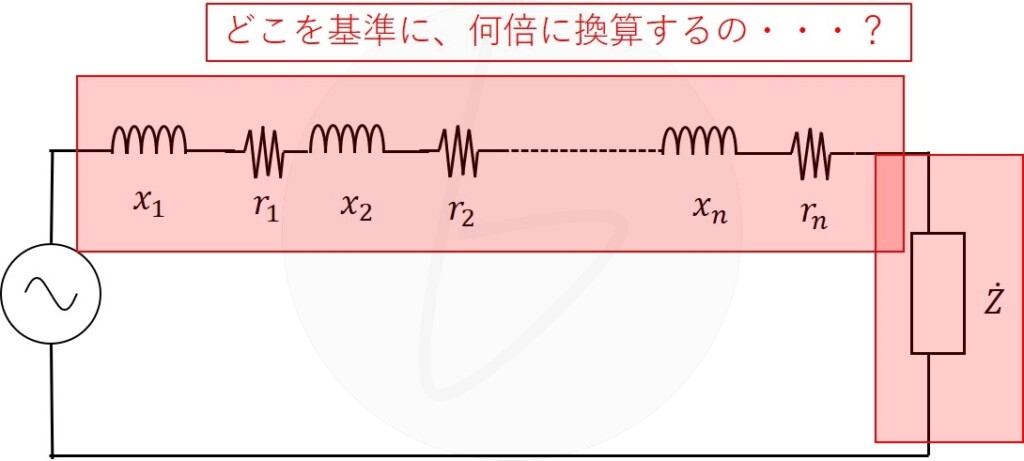
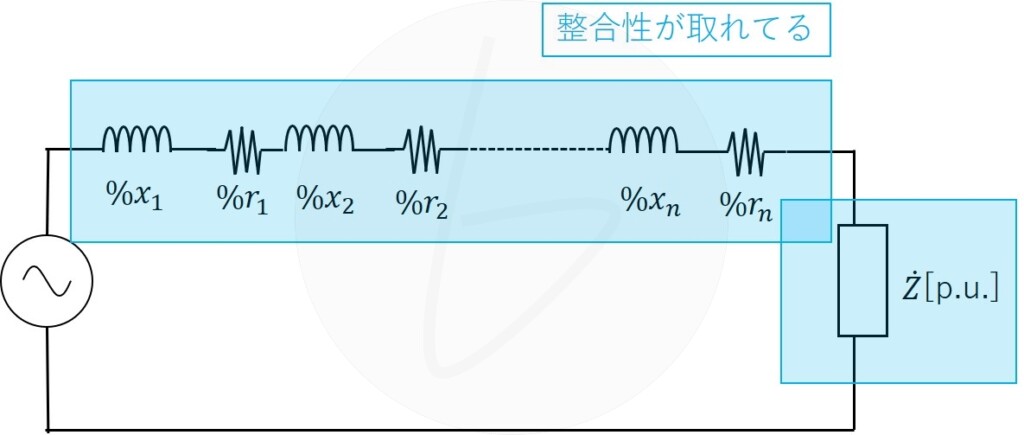
一方、単位法であれば基準容量に対してすべてをそろえるので、電圧の違いを考える必要がありません。
そして、計算したい場所で決められている定格電圧を1[p.u.]として計算すればOKということになり、シンプルな計算ができます。
まとめ
ここまで、単位法の概念について説明してきました。
単位法はあくまでも概念的なものですので、説明しきれない部分も多いです。
言いたいこととしては、ここで説明した内容が基本となる概念です。
最初のうちは、
そんなものなんだ
と思って、問題集などで単位法の問題に取り組んでみてください。
最終的に感覚でつかむことが大切ですし、多くの問題を解く中で、単位法だから簡単に解ける問題もあり、だんだんと単位法の意味が理解できてきます。
最終的には電圧の異なる電力系統の連系について、電圧差を考えずに一つの回路で描き表すところに、単位法のうまみがあります。
知れば知るほど面白い単位法。
ぜひ、使いこなしてください。
以上、単位法について、参考になれば幸いです。