みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、変圧器の特性試験である、
- 無負荷試験
- 短絡試験
の理解の方法について紹介します。
これらの試験について、テストなどで突然試験結果が与えられ、
何が何を示しているのかがわからない・・・!
となることが多いと思います。
そこで、等価回路ベースで理解する方法について紹介します。
そもそもですが、これらの試験の目的は、変圧器の等価回路の回路定数の算定のために行うものです。
したがって、問題で与えられたとおりに等価回路に条件を与え、電流経路を追うだけで、
- 銅損を見ているのか
- 鉄損を見ているのか
が判定できます。
▼おすすめ記事▼

変圧器の特性試験
変圧器の特性試験には、
- 無負荷試験
- 短絡試験
があります。
・無負荷試験
1次側、または2次側の一方を開放することで、負荷電流を0Aにします。
その時の電力や電流を測定することで、励磁回路での損失、つまり励磁回路の回路定数がわかります。
・短絡試験
1次側、または2次側の一方を開放することで、非常に大きい負荷電流(一般的には定格電流)を流す試験です。
その時、変圧器には負荷電流と励磁電流の両方が流れます。
しかし、励磁電流は定格負荷電流よりも非常に小さく無視できるので、電力や電流を測定することで、巻線の抵抗値を測定できます。
無負荷試験の等価回路
無負荷試験では、一般的には2次側に電源をつなぎ、1次側を開放するようです。
しかし、1次側、2次側のどちらを開放するかは本質的な問題ではなく、電流経路が重要になります。
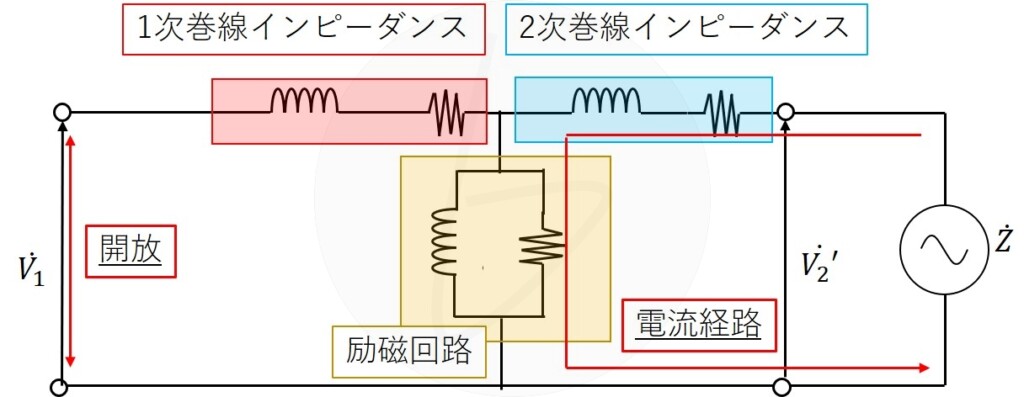
下の回路図は、変圧器のT型等価回路における無負荷試験の電流経路です。
1次側は開放しているため、回路上には励磁電流しか流れません。
ここで、2次側巻線インピーダンスは、励磁回路のインピーダンスよりも非常に小さいため無視できます。
この無負荷試験で、
- 消費電力[kW]から、オームの法則よりコンダクタンス成分を計算可能
- 電圧と電流のベクトル計算からアドミタンスが計算可能
- アドミタンスとコンダクタンスよりサセプタンスが計算可能
となり、励磁回路の回路定数を計算できるようになります。
短絡試験の等価回路
短絡試験は、一般的に2次側を短絡し、1次側に電圧を印加することで行います。
変圧器のT型等価回路で、電流経路を見ると下のようになります。
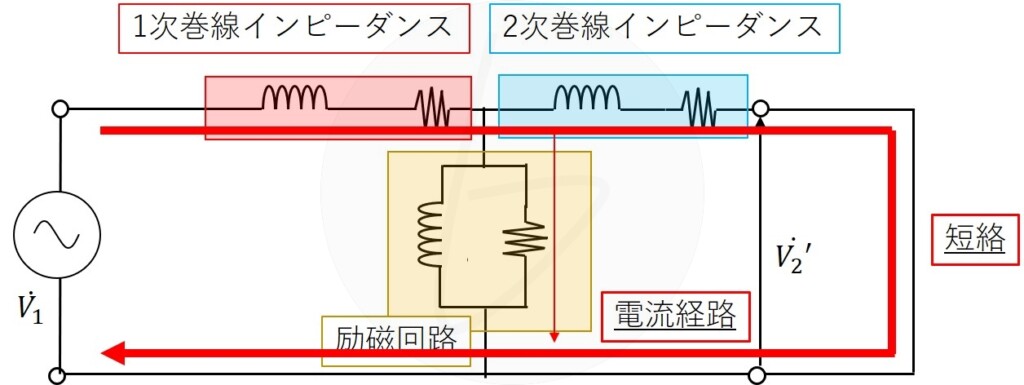
矢印の太さは電流の相対的な大きさを示しています。
つまり、短絡電流に対して励磁電流は非常に小さく、無視することができます。
この時、短絡試験では、
- 消費電力[kW]と電圧からオームの法則より巻線抵抗(1次換算値)を計算可能
- 電圧と電流のベクトル計算から巻線のインピーダンス(1次換算値)が計算可能
- インピーダンスと抵抗値からリアクタンスが計算可能
となり、巻線回路の回路定数が計算できます。
まとめ
ここまで、変圧器の特性試験について紹介してきました。
- 無負荷試験
- 短絡試験
など、突然試験結果を提示され、何が何だか分からなくなることもあると思います。
そんな時には、必ず等価回路まで戻ってください。
等価回路上で意味することを考えれば、意外にも単純な話になっています。
特性試験の問題があれば、得点源になると思えるぐらい、基礎を磨いてみると、また世界観が変わってきます。
なお、変圧器の特性試験によって変圧器等価回路の各パラメーターを求めることができます。
変圧器の回路定数が分かれば、変圧器の効率を計算したり、最大効率(鉄損=銅損にする運転)がどの程度の者か、計算できたりします。
その他、計算はややこしいですが、電圧変動率を求めたりすることもできます。
併せて参考にしてください。
以上、変圧器の特性試験について、参考になれば幸いです。