みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
- 今回は、同期機において、
- 同期インピーダンス
- 短絡比
- 無負荷飽和曲線
- 三相短絡曲線
について説明します。
これらは、基本的には同期機の定義に近い部分であり、暗記事項です。
また、パーセント同期インピーダンスは、変圧器のパーセントインピーダンスと同じ意味であり、単位法を使用する際に重要な概念になります。
単位法について理解が難しいと感じる方は、単位法の概念の解説記事をご覧ください。
▼おすすめ記事▼
ポイント
短絡比
短絡比は基準電流の何倍の短絡う電流が流れるかを示す値のこと。
後述の無負荷飽和曲線と三相短絡曲線の組み合わせによって、界磁電流から短絡比を求めることも可能。
短絡比$k$について、
$$k=\frac{I_s}{I_n}=\frac{1}{\%Z_s[\rm{p.u.}]}=\frac{I_{f2}}{I_{f1}} \tag{1}$$
ただし、
- $\%Z_s$:パーセント同期インピーダンス[p.u.]
- $I_{n}$:定格電流
- $V_{n}$:定格電圧
- 定格電流に等しい短絡電流を流す界磁電流$I_{f1}$
- 定格電圧に等しい無負荷誘導起電力を発生させる界磁電流$I_{f2}$
無負荷飽和曲線
無負荷飽和曲線は、同期発電機を無負荷のまま回転させ、徐々に界磁電流を増加させたときの端子電圧の変化を示すグラフ。
最初のうちは界磁電流とともに磁束が増加し、比例するように端子電圧も増加するが、徐々に磁気飽和し端子電圧の上昇が緩やかになるため、頭打ちするグラフとなる。
三相短絡曲線
三相短絡曲線は、同期発電機を短絡した状態で定格速度で運転した場合、界磁電流を徐々に増加させたときに流れる短絡電流の値を示すグラフ。
一般的に直線となる。
同期インピーダンスと短絡比
同期インピーダンス
同期機には、
- 同期リアクタンス(漏れリアクタンス+電機子反作用リアクタンス)
- 巻線の抵抗値
のベクトル和となる、同期インピーダンスがあります。
同期インピーダンスは、図1に示す同期機の等価回路において、
$$Z_s=r_a+jx_s \tag{2}$$
で示されます。
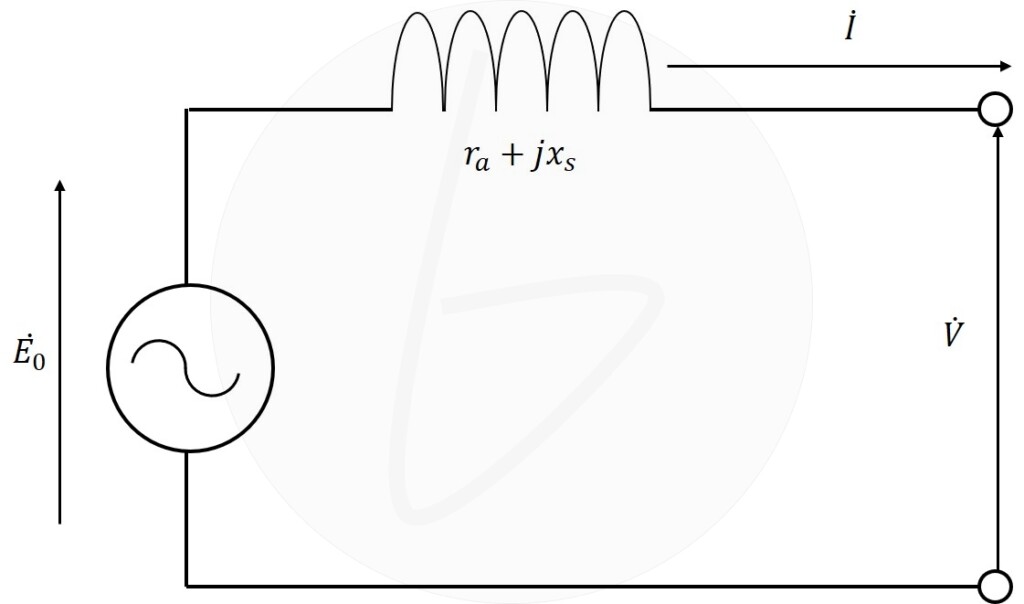
図1 同期発電機の等価回路
同期インピーダンスも、インピーダンス電圧$Z_sI_n$を計算したのち、定格電圧との比をとって、パーセント同期インピーダンス$%Z_s$が計算でき、
$$\%Z_s=\frac{Z_sI_{n}}{V_{n}}×100 \tag{3}$$
となります。
ここで、
- $Z_s$:同期インピーダンス
- $I_{n}$:定格電流
- $V_{n}$:定格電圧
短絡比
短絡比$k$とは、同期発電機の無負荷端子電圧が定格電圧に等しいとき、三相短絡時させた場合、定格電流に対して何倍の短絡電流が流れるかを示すものであり、定義通りに、
$$k=\frac{I_s}{I_{n}} \tag{4}$$
で示されます。
では、回路計算から短絡比とパーセント同期インピーダンスの関係を見ていきます。
三相短絡電流は、三相平衡負荷となるので、三相のうち一相のみを取り出して、単相交流回路で取り扱えます。
そして、無負荷端子電圧とは、電流が0のときの端子電圧のことを言います。
つまり無負荷端子電圧が端子電圧に等しいとは、電流が0であり同期インピーダンスによる電圧降下が生じないことを考えれば、無負荷誘導起電力$\dot{E_0}$が定格電圧$\dot{V_n}$に等しいと言い換えることができます。
この状況を電気回路で表現すれば、図2のようになります。
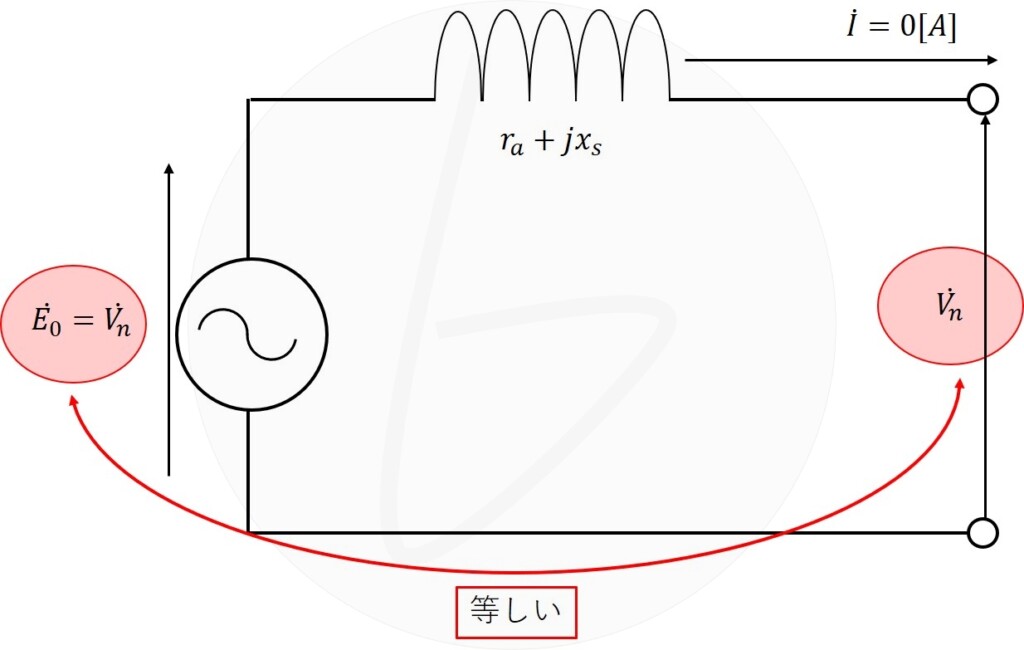
図2 短絡比を定義する等価回路
そして、図のように両端を短絡することで流れる電流が、短絡電流です。
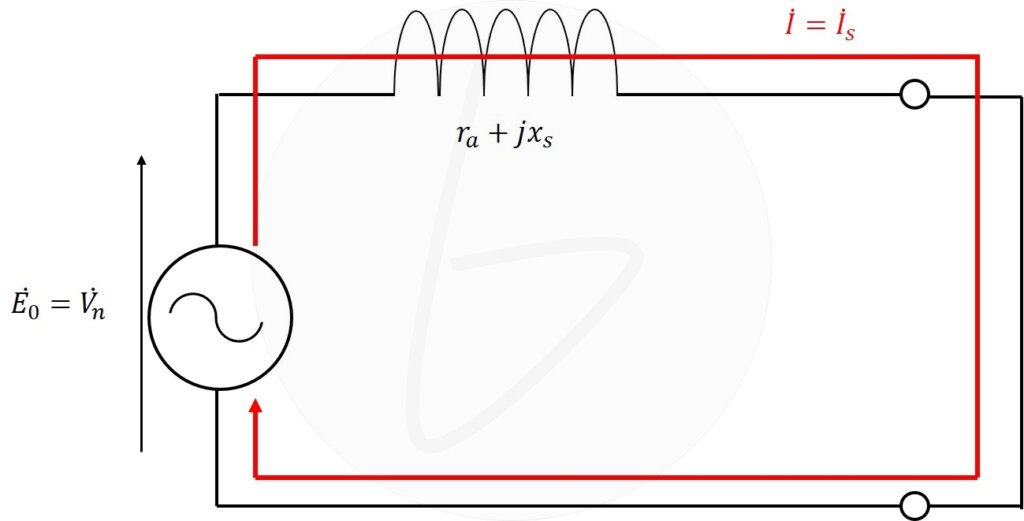
図3 短絡電流の計算
ここで、三相短絡時の回路図から短絡電流を計算すると、
$$I_s=\frac{V_{n}}{Z_s} \tag{5}$$
となります。
式(4)と式(5)から、
$$k=\frac{\frac{V_{n}}{Z_s}}{I_{n}} \tag{6}$$
であり、また単位法の定義から、基準インピーダンス$Z_n$について、
$$Z_{n}=\frac{V_{n}}{I_{n}} \tag{7}$$
であることを考えると、式(6)は、
$$k=\frac{Z_{n}}{Z_s}=\frac{1}{\%Z_s} \tag{8}$$
となります。
式(8)において、同期インピーダンス$Z_s$と基準インピーダンス$Z_n$の比率は、パーセント同期インピーダンス$\%Z_s$[p.u.]であり、
$$\%Z_s[\rm{p.u.}]=\frac{Z_s}{Z_n}$$
であることを利用しています。
すなわち、同期インピーダンスを単位法[p.u.]値で表した場合の逆数が、短絡比になります。
言い換えれば、短絡電流は、定格電流×同期インピーダンス[p.u.]の逆数倍だけ流れるということになります。
この考え方は、電力・管理分野における、電力系統の三相短絡事故電流の計算で役立つ考えです。
幅広く役立つ知識ですから、ややこしい部分はありますが、きっちりと理解しておきましょう。
無負荷飽和曲線と三相短絡曲線、短絡比の関係
無負荷飽和曲線と三相短絡曲線
同期機の重要な特性グラフとして、
- 無負荷飽和曲線
- 三相短絡曲線
があります。
無負荷飽和曲線と三相短絡曲線は、下のようなグラフになります。
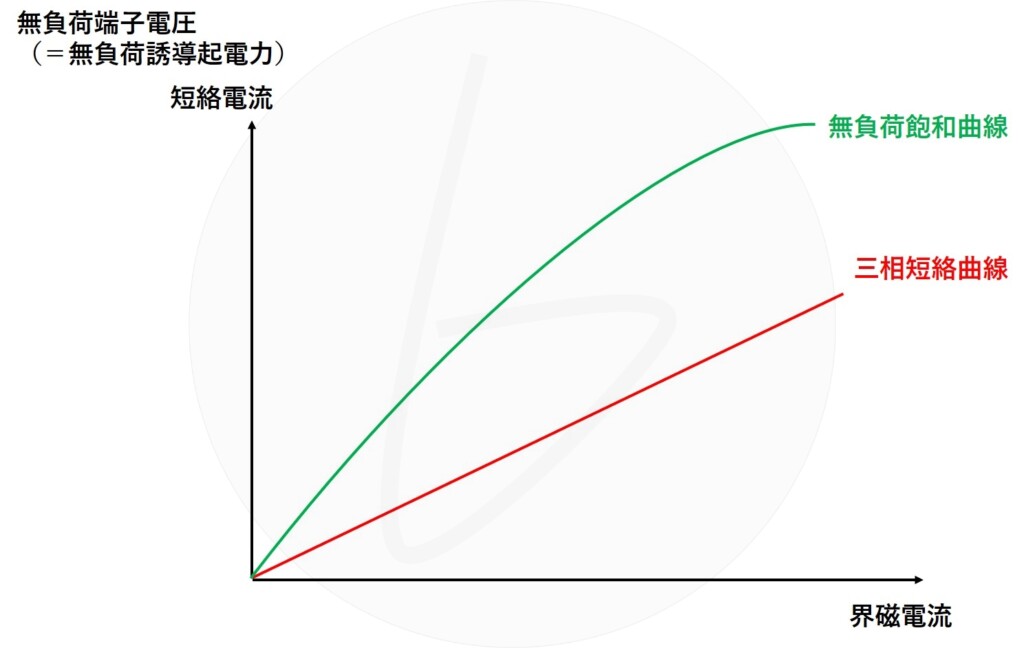
図4 同期発電機の無負荷飽和曲線と三相短絡曲線
■無負荷飽和曲線
同期発電機を無負荷・定格速度で運転したとき、界磁電流を徐々に増した時の無負荷端子電圧(負荷電流が0、すなわち無負荷誘導起電力に同じ)の変化を示したグラフです。
界磁電流を増した時、最初のうちは磁界も直線的に増加するため、無負荷端子電圧も直線的に上昇しますが、鉄心はいずれ磁気飽和するので、ある一定のところから徐々に頭打ちのある飽和曲線になります。
■三相短絡曲線
同期発電機の端子を短絡させた状態で定格速度で運転し、短絡電流を流します。
その時、界磁電流を変化させることで、短絡電流がどのように変化するかを示すものが、三相短絡曲線です。
三相短絡曲線とはなっていますが、直線で示される特性になります。
界磁電流から短絡比を求める
では、無負荷飽和曲線と三相短絡曲線から短絡比を界磁電流から求めれるか考察してみましょう。
短絡比は、もともと、無負荷端子電圧(=無負荷誘導起電力)が定格電圧に等しい状況で、三相短絡を行ったときに流れる短絡電流に対して、
$$短絡比=\frac{短絡電流}{定格電流} \tag{9}$$
と定義されていました。
ですが、無負荷飽和曲線と三相短絡曲線を組み合わせれば、界磁電流から短絡比を求めることができます。
ポイントになるのは、三相短絡曲線において、界磁電流と短絡電流の関係が直線になることであり、これより、
$$界磁電流の比率=短絡電流の比率 \tag{10}$$
が計算できます。
以後の説明で、うまく直線関係に乗せるところを重点的にチェックしてみてください。
まず、
無負荷時に端子に定格電圧を生じさせるためには、無負荷飽和曲線において定格電圧$V_n$に着目します。
この時、
- 三相短絡曲線との交点が短絡電流$I_s$(グラフ中の①)
- 短絡比の定義を満たす条件を作る界磁電流が$I_{f2}$(グラフ中の②)
となります。
その時の界磁電流で三相短絡曲線を見ると、示している短絡電流$I_s$は、まさに、「無負荷端子電圧(=無負荷誘導起電力)が定格電圧に等しい状況で、三相短絡を行ったときに流れる短絡電流」であることがわかると思います。
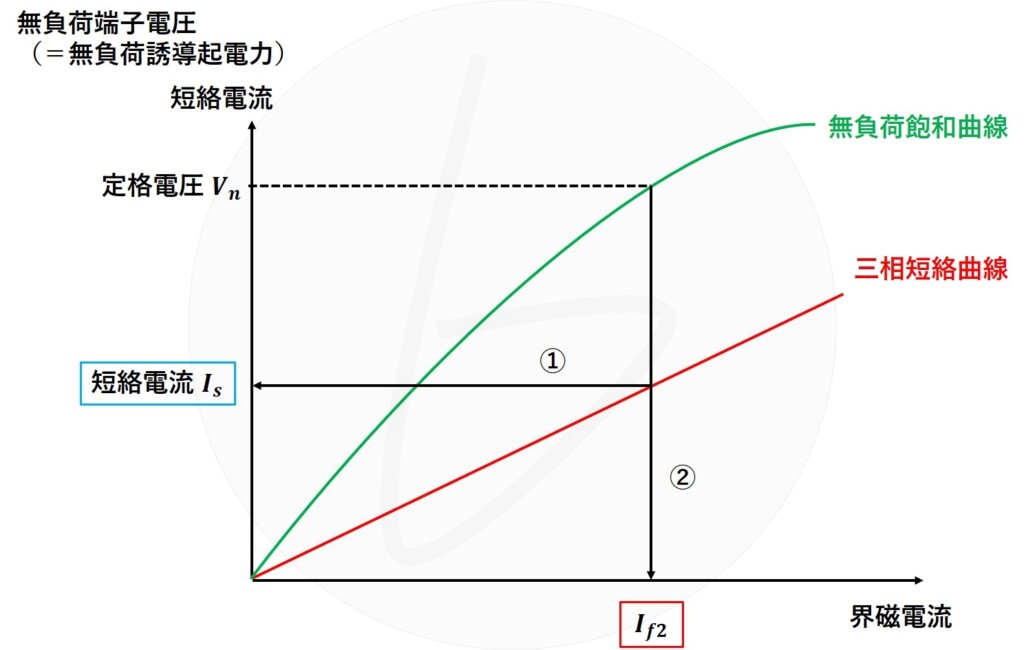
図5 無負荷飽和曲線と三相短絡曲線から短絡比を求める方法①
次に、三相短絡曲線に着目し、縦軸(短絡電流)から、定格電流$I_n$を探します(グラフ中③)。
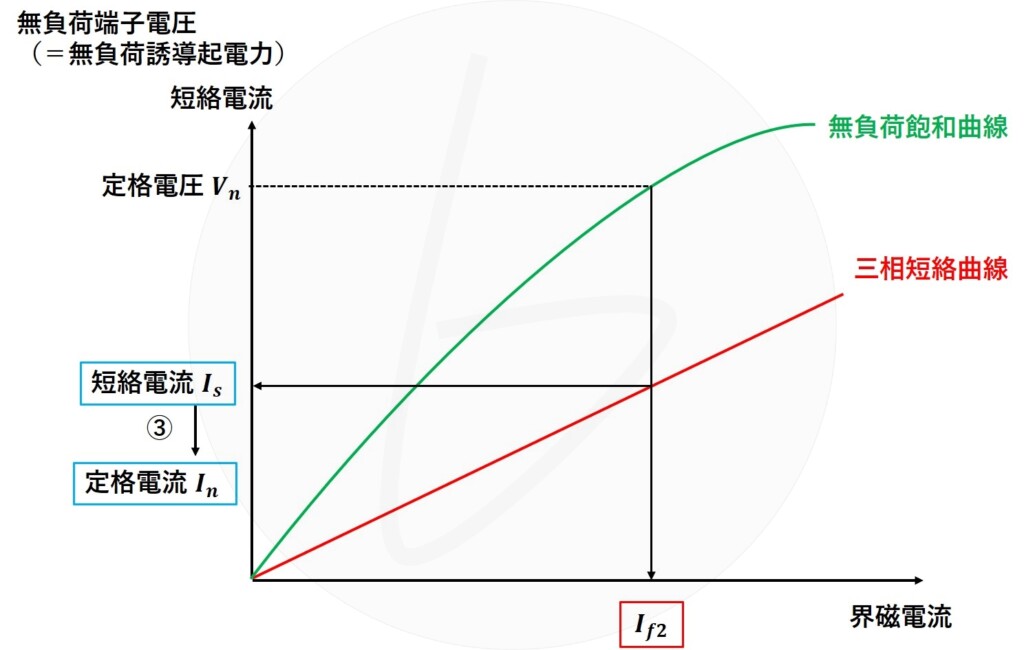
図5 無負荷飽和曲線と三相短絡曲線から短絡比を求める方法②
その時の界磁電流$I_{f1}$を読みます(グラフ中④)。
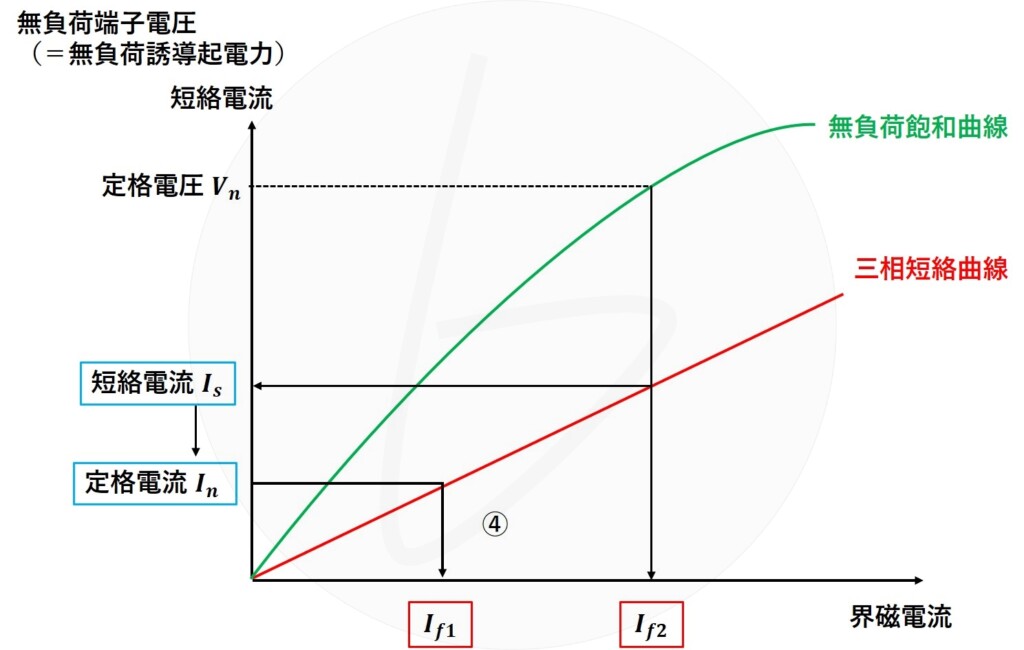
図5 無負荷飽和曲線と三相短絡曲線から短絡比を求める方法③
さて、三相短絡曲線は、直線関係にあります。
すると、負荷電流に関して$I_s$と$I_n$の比率は、界磁電流$I_{f1}$と$I_{f2}$の比率と等しい、つまり、短絡比$k$について、
$$k=\frac{I_s}{I_n}=\frac{I_{f2}}{I_{f1}} \tag{11}$$
ということができます。
式(11)を使えば、界磁電流から短絡比を求めることができます。
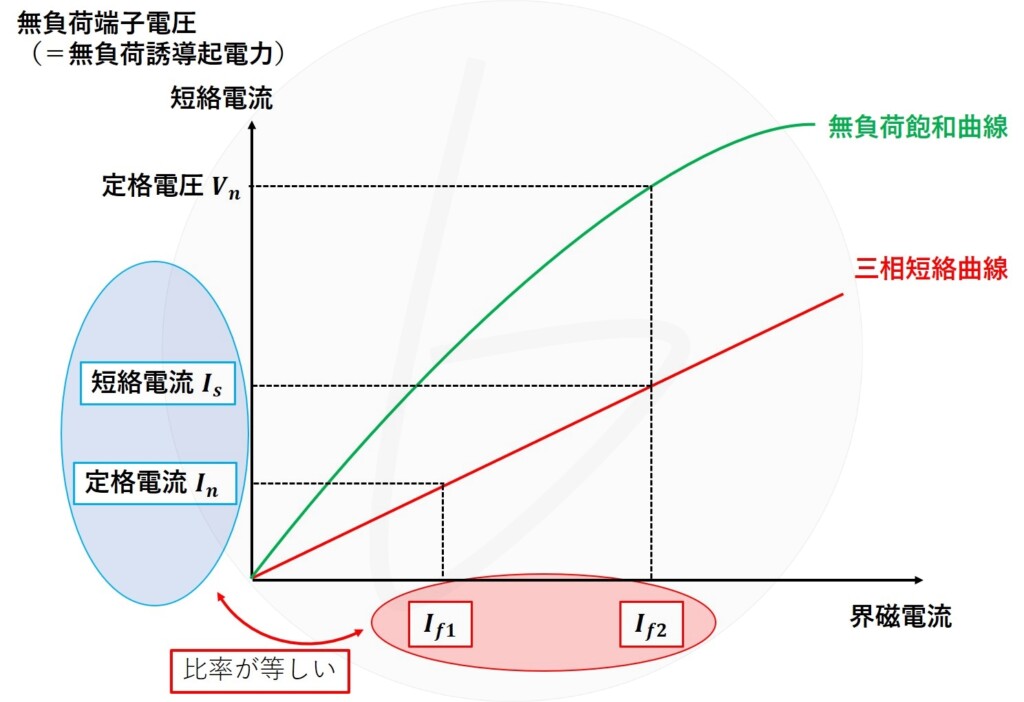
図5 無負荷飽和曲線と三相短絡曲線から短絡比を求める方法④
以上の結果から、界磁電流によって短絡比を求める場合、
- 定格電流に等しい短絡電流を流す界磁電流$I_{f1}$
- 定格電圧に等しい無負荷誘導起電力を発生させる界磁電流$I_{f2}$
がわかれば、短絡比の計算や、定格電流に対して何倍の短絡電流が流れるか、などの計算ができます。
同期機の短絡に関する問題で、様々な条件下での界磁電流の条件が与えられたら、以上の説明をもとに、界磁電流から答えを導く方法を考えてみましょう。
まとめ
ここまで、同期機の暗記事項として、
- 同期インピーダンス$Z_s$
- %同期インピーダンス$\%Z_s$
- 短絡比($k=\frac{I_s}{I_n}=\frac{1}{\%Z_s[\rm{p.u.}]}=\frac{I_{f2}}{I_{f1}}$)
- 無負荷飽和曲線(=飽和する曲線)
- 三相短絡曲線(=直線関係)
について説明してきました。
同期機については、基本的にはベクトル図を用いて回答するパターンが多いのですが、稀にこうした界磁電流を絡めた問題が出題されます。
計算自体は難しくないので、確実に回答できるようになっておきましょう。
以上、同期機の基本特性について参考になれば幸いです。