みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、三相誘導電動機の特性計算について解説します。
三相誘導電動機は、変圧器をベースに等価回路を作成することができます。
この記事では、三相誘導電動機の等価回路をベースに、
- 2次入力
- 2次銅損
- 機械的出力
- トルク
といった、三相誘導電動機の特性計算について、説明していきます。
三相誘導電動機の特性計算の式は、今後説明する比例推移でも役立つものです。
▼おすすめ記事▼
三相誘導電動機の等価回路における回路定数の意味
先ほどのL型等価回路では、回路定数と機械出力の関係が不明確でした。
そのため、通常は以下のような回路で考えます。
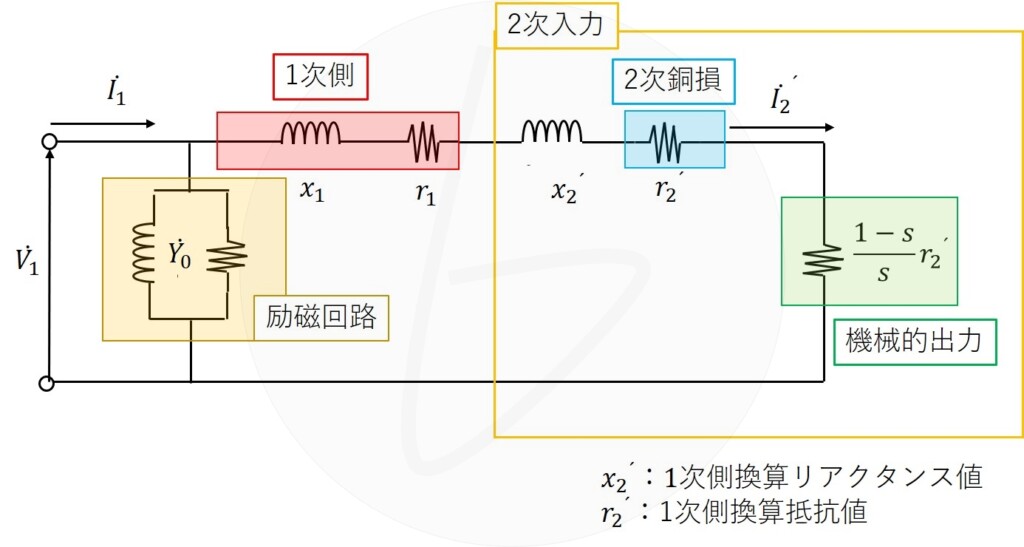
ここで、
- 2次回路入力:$3{I_2´}^2\frac{1}{s}r_2´$
- 2次銅損:$3{I_2´}^2r_2´$
となります。
誘導電動機として動作する場合には0≦s≦1なので、常に、
2次回路入力≧2次銅損
の関係が成立しています。
分母にsが入っていて大小関係に迷うかもしれませんが、sは1以下になるので、直感的な大小関係とは逆になるのがポイントですね。
以上より、機械的出力はこの差分であり、
$$3{I_2´}^2\frac{1}{s}r_2´-3{I_2´}^2r_2´$$
すなわち、
$$3{I_2´}^2\frac{1-s}{s}r_2´$$
であるとわかります。
これが上の回路図において緑で囲んだ機械的出力になります。
三相誘導電動機の特性計算
さて、等価回路さえわかれば、誘導電動機の特性計算は簡単に求まります。
なお、誘導電動機は基本的には三相であることが前提なので、
- 出力において3倍
- Vは相電圧(線間電圧の$\frac{1}{\sqrt{3}}$倍)
を忘れないようにしてください。

■2次電流$I_2´$
励磁回路を無視すると、
$$I_2´=\frac{V}{\sqrt{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)^2}}$$
となります。
再度書きますが、式の中の$V$は相電圧です。
問題文で線間電圧が与えられた場合には、$\frac{1}{\sqrt{3}}$倍を忘れないようにしてください。
■2次入力$P_2$(回転子に加わるエネルギー)
$P_2=3{I_2´}^2\frac{1}{s}r_2´$であるから、
$$P_2=3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}\frac{1}{s}r_2´$$
■2次銅損
$P_{2c}=3{I_2´}^2r_2´$であるから、
$$P_2=3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}r_2´$$
■機械出力
$P_o=3{I_2´}^2\frac{1-s}{s}r_2´$であるから、
$$P_o=3\frac{V^2}{(x_1+x_2´)^2+(r_1+\frac{1}{s}r_2´)}\frac{1-s}{s}r_2´$$
■トルク$T$
同期角速度を$\omega_0$とすると、
$$T=\frac{P_0}{(1-s)\omega_0}$$
同時に、$P_0=(1-s)P_2$であることもわかるから、
$$T=\frac{P_2}{\omega_0}$$
ともなります。
誘導電動機の基本式は上記のとおりです。
こうして見てみると、$s$や$1-s$の違いだけで、なんだか似た式が多いことに気づくでしょう。
これらを組み合わせることで、回路定数が不明な場合でも、すべりsを含めた比率の関係でうまく回答できる問題が多いです。
解法をパターン化せず、臨機応変に対応できるように、式変形に慣れておくことが大切です。
これらの式は、誘導電動機の等価回路さえわかっていればすぐに導ける関係式です。
なので、本来であれば覚える必要はありません。
式の暗記よりも、誘導電動機の等価回路の理解に力を入れたほうが、応用力も養え、効率がいいです。
まとめ
ここまで、三相誘導電動機の特性計算について解説してきました。
三相誘導電動機の特性は、等価回路の意味を理解できれば、あとは普通の電気回路の計算になります。
特性計算の式は暗記するのではなく、必ず等価回路上から考えて都度考えるようにすれば応用力が養われるでしょう。
また、今後の比例推移を考える基礎にもなるので、$\frac{r_2´}{s}$の項にも注目しておいてください。
以上、三相誘導電動機の特性計算について、参考になれば幸いです。