同期発電機の並行運転（並列運転）時の負荷分担と循環電流について

みなさん、こんにちは！

ブリュの公式ブログ.org（for Academic Style）にお越しいただきまして、ありがとうございます！

今回は、同期発電機の並行運転（並列運転）について、

• 負荷分担
• 循環電流

について説明します。

同期発電機 並行運転（並列運転）時の負荷分担

循環電流がある場合

同期発電機Aと同期発電機Bが並行運転を行い、端子電圧$\dot{V}$で負荷に電流$\dot{I}$を供給しているとき、同期発電機Aの供給する電流$\dot{I_A}$、同期発電機Bの供給する電流$\dot{I_B}$、循環電流$\dot{I_{roop}}$は、

$$\begin{cases}
{\rm 同期発電機A：} \dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}+\dot{I_{roop}}\\
{\rm 同期発電機B：} \dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}-\dot{I_{roop}}\\
{\rm 循環電流：} \dot{I_{roop}}=\frac{\dot{E_{0A}}-\dot{E_{0B}}}{\dot{Z_A}+\dot{Z_B}}
\end{cases}\tag{1}$$

となる。

ただし、

• $\dot{E_{0A}}$：同期発電機Aの無負荷誘導機電力
• $\dot{Z_A}$：同期発電機Aの同期インピーダンス
• $\dot{E_{0B}}$：同期発電機Bの無負荷誘導起電力
• $\dot{Z_B}$：同期発電機Bの同期インピーダンス

循環電流がない場合

循環電流$\dot{I_{roop}}$がない場合、すなわち$\dot{E_{0A}}=\dot{E_{0B}}$の場合、

$$\begin{cases}
{\rm 同期発電機A：} \dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}\\
{\rm 同期発電機B：} \dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}
\end{cases}\tag{2}$$

となる。

同期発電機の負荷分担の導出

循環電流を考慮する場合

2台の同期発電機がある負荷に電力を送電している場合を考えると、電流経路としては、図1に示す通り、

• 同期発電機Aの供給する電流：$\dot{I_A}$
• 同期発電機Bの供給する電流：$\dot{I_B}$

があり、それらの電流の和が負荷電流$\dot{I}$であり、

$$\dot{I}=\dot{I_A}+\dot{I_B} \tag{3}$$

になります。

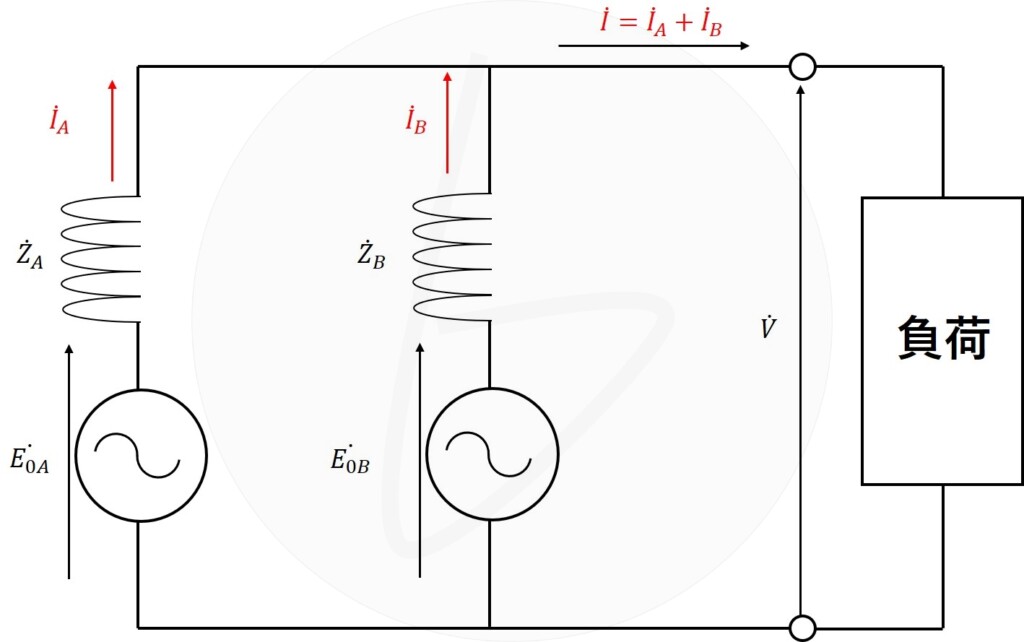
図1 同期発電機の並列運転時における電流経路

さて、端子電圧を$\dot{V}$とすれば、同期発電機Aに関する回路方程式として、

$$\dot{E_{0A}}=\dot{Z_A} \dot{I_A}+\dot{V} \tag{4}$$

が成り立ち、同様に同期発電機Bについても、

$$\dot{E_{0B}}=\dot{Z_B} \dot{I_B}+\dot{V} \tag{5}$$

が成り立ちます。

これで、式(3)、式(4)、式(5)の3つを連立すれば、解くことができます。

式(4)と式(5)で端子電圧$\dot{V}$を消去すれば、

$$\dot{E_{0A}}-\dot{Z_A} \dot{I_A}=\dot{E_{0B}}-\dot{Z_B} \dot{I_B} \tag{6}$$

$$\dot{I_B}=\frac{1}{\dot{Z_B}} \left( \dot{Z_A} \dot{I_A} -\left( \dot{E_{0A}}-\dot{E_{0B}} \right) \right) \tag{7}$$

式(3)から、

$$\dot{I}=\dot{I_A}+\frac{1}{\dot{Z_B}} \left( \dot{Z_A} \dot{I_A} -\left( \dot{E_{0A}}-\dot{E_{0B}} \right) \right) \tag{8}$$

$$\dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}+\frac{\dot{E_{A0}}-\dot{E_{B0}}}{\dot{Z_A}+\dot{Z_B}} \tag{9}$$

また、$\dot{I_B}$について、

$$\begin{align}
\dot{I_B}&=\dot{I}-\dot{I_A}\\
&=\dot{I}-\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}+\frac{\dot{E_{A0}}-\dot{E_{B0}}}{\dot{Z_A}+\dot{Z_B}}\\
&=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}-\frac{\dot{E_{A0}}-\dot{E_{B0}}}{\dot{Z_A}+\dot{Z_B}} \tag{10}
\end{align}$$

となります。

よって、

$$\begin{cases}
{\rm 同期発電機A：} \dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}+\frac{\dot{E_{A0}}-\dot{E_{B0}}}{\dot{Z_A}+\dot{Z_B}}\\
{\rm 同期発電機B：} \dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}-\frac{\dot{E_{A0}}-\dot{E_{B0}}}{\dot{Z_A}+\dot{Z_B}}
\end{cases}\tag{11}$$

となります。

循環電流の計算

次に、同期発電機の間をループする循環電流$\dot{I_{roop}}$について計算します。

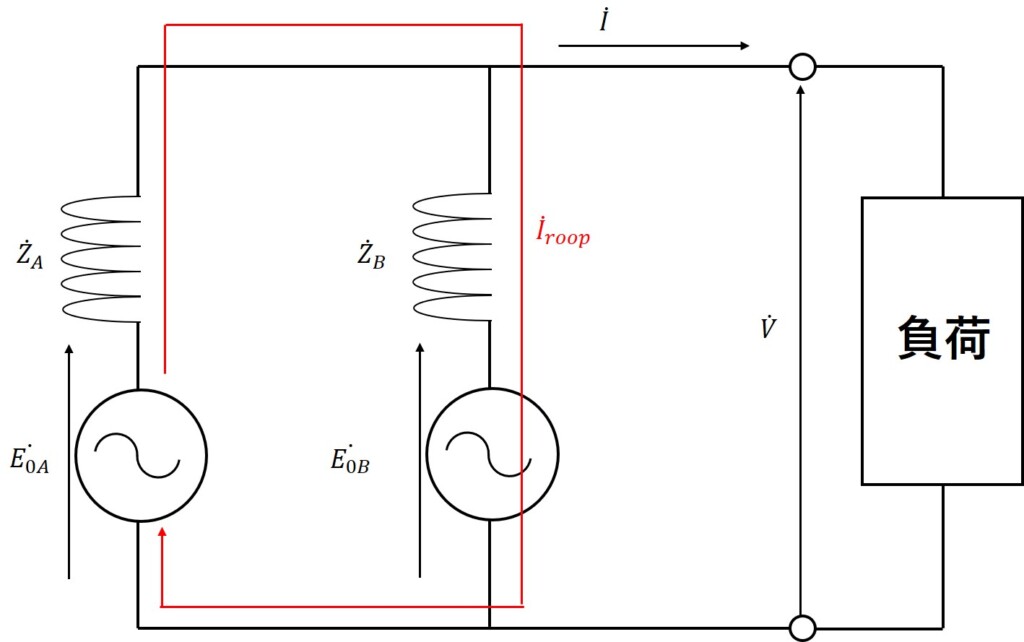
図2 同期発電機の並行運転 循環電流の計算

$\dot{I_{roop}}$の流れる経路における回路方程式より、

$$\dot{E_{0A}}-\dot{E_{0B}}=\dot{I_{roop}}(\dot{Z_A}+\dot{Z_B}) \tag{12}$$

であり、

$$\dot{I_{roop}}=\frac{\dot{E_{0A}}-\dot{E_{0B}}}{\dot{Z_A}+\dot{Z_B}} \tag{13}$$

となります。

つまり、同期発電機の負荷分担における式(11)は、

$$\begin{cases}
{\rm 同期発電機A：} \dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}+\dot{I_{roop}}\\
{\rm 同期発電機B：} \dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}-\dot{I_{roop}}\\
{\rm 循環電流：} \dot{I_{roop}}=\frac{\dot{E_{0A}}-\dot{E_{0B}}}{\dot{Z_A}+\dot{Z_B}}
\end{cases}\tag{14}$$

とも表記できます。

また、無負荷誘導起電力$\dot{E_{0A}}$と$\dot{E_{0B}}$が等しく、

$$E_{0A}=\dot{E_{0B}} \tag{15}$$

の関係があれば、

$$\dot{I_{roop}}=0 \tag{16}$$

となるので、

$$\begin{cases}
{\rm 同期発電機A：} \dot{I_A}=\frac{\dot{Z_B}}{\dot{Z_A}+\dot{Z_B}}\dot{I}\\
{\rm 同期発電機B：} \dot{I_B}=\frac{\dot{Z_A}}{\dot{Z_A}+\dot{Z_B}}\dot{I}
\end{cases}\tag{17}$$

となって、単にインピーダンスの逆比に従って負荷を分担することもわかります。

まとめ

ここまで、同期発電機の並行運転時における負荷分担について説明してきました。

同期発電機の等価回路が理解できていれば、比較的単純な交流回路の計算問題になります。

関連コンテンツ

関連記事

電気機器（変圧器/誘導機/同期機/直流機）の記事一覧はこちら

→電気機器 記事一覧

本のご案内

ブリュの公式ブログでは書籍を出版しています。

本記事で紹介した、同期発電機の並行運転（並列運転）については、以下の本に記載しています。