みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、三相交流の電力測定を、2個の電力計で行う二電力計法の原理について説明します。
ベクトル図が登場しややこしい部分はありますが、最後に三角関数の加法定理で余計な位相の情報が消去されるところは爽快なので、ぜひ最後まで読んでください。
二電力計法における電力系の接続法
二電力計法では、図に示す通りにある特定の相を起点として、残りの相との間の電力を測定します。
下は例として、c相を起点とし、
- a-c間の電力
- b-c間の電力
を測定しています。
この時、三相の電力$W$は、単純に、
$$W=W_1+W_2$$
で計算できるのですが、その理由を見ていきます。
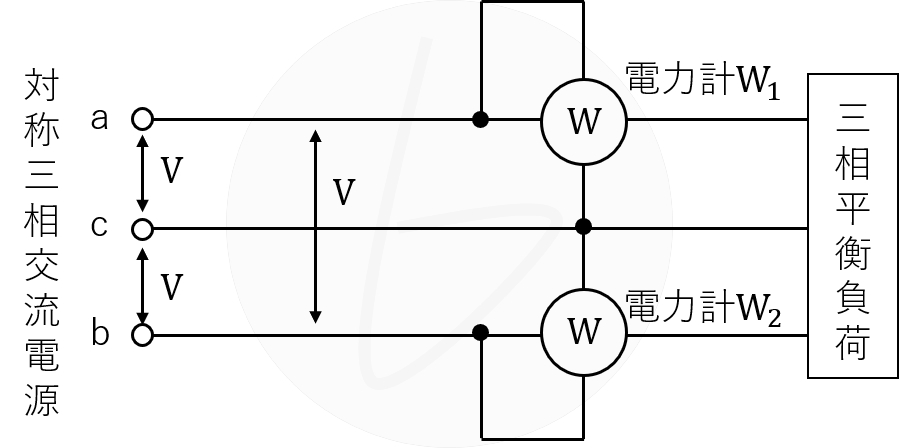
図1 二電力計法における電力系の接続の例
ベクトル図による計算
対称三相交流回路におけるベクトル図を図2に示します。
ここで、$\dot{E_a}$、$\dot{E_b}$、$\dot{E_c}$は相電圧を示し、$\dot{I_a}$、$\dot{I_b}$、$\dot{I_c}$は各相に流れる電流を示します。
力率$theta$は、各相の相電圧と電流の位相差なので、図2に示す通りになります。
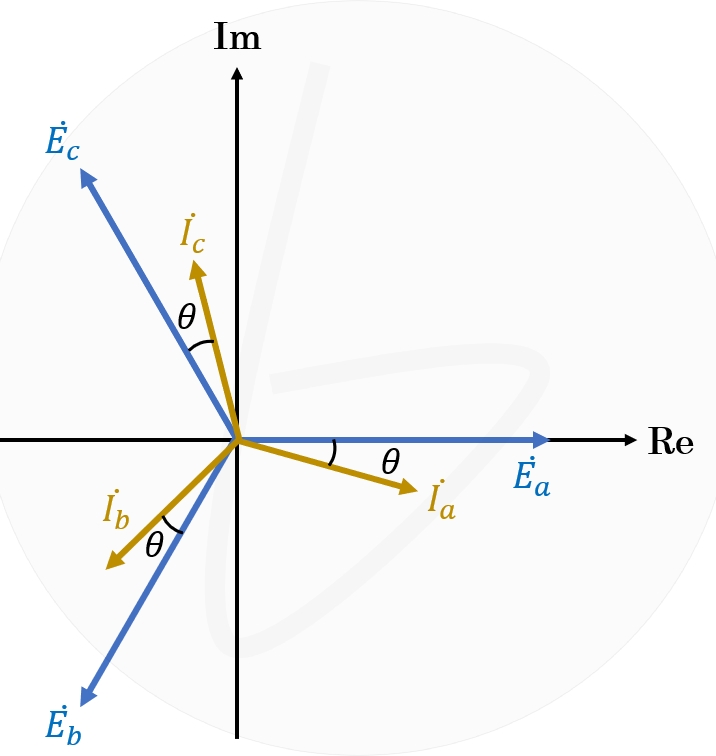
図2 対称三相交流回路における相電圧と電流及び力率
ここで、c相を起点とした線間電圧を考えれば、図3のようになります。
$\dot{V_{ac}}$はa-c間の線間電圧ベクトル、$\dot{V_{bc}}$はb-c間の線間電圧ベクトルです。
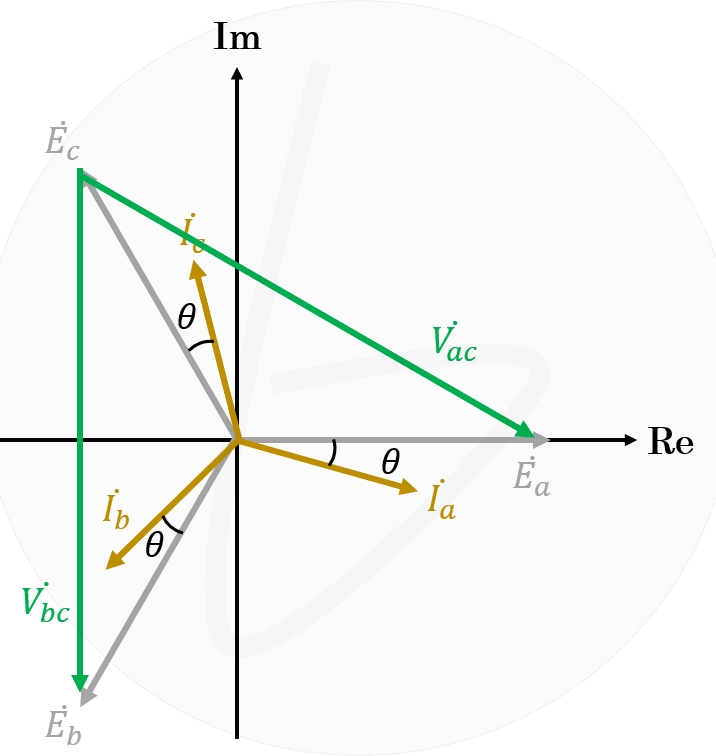
図3 c相を起点とした線間電圧ベクトル
さらに、線間電圧ベクトル$V_{ac}$と$V_{bc}$の起点を原点に移動させると、図3に示す通りになります。
ここで、電圧計$W_1$は$\dot{V_{ac}}$と$\dot{I_a}$を測定し、電圧計$W_2$は$\dot{V_{bc}}$と$I_b$を測定しています。
つまり、相電圧と線間電圧の位相差も考えれば、
$$\begin{cases}
W_1=V_{ac}I_acos\left(30°-\theta\right)\\
W_2=V_{bc}I_ccos\left(\theta+30°\right)
\end{cases}$$
さらに
対称三相交流回路であることから、
$$V=V_{ac}=V_{bc}$$
及び、
$$I=I_a=I_b$$
であることより、
$$\begin{cases}
W_1=VIcos\left(30°-\theta\right)\\
W_2=VIcos\left(\theta+30°\right)
\end{cases}$$
となります。
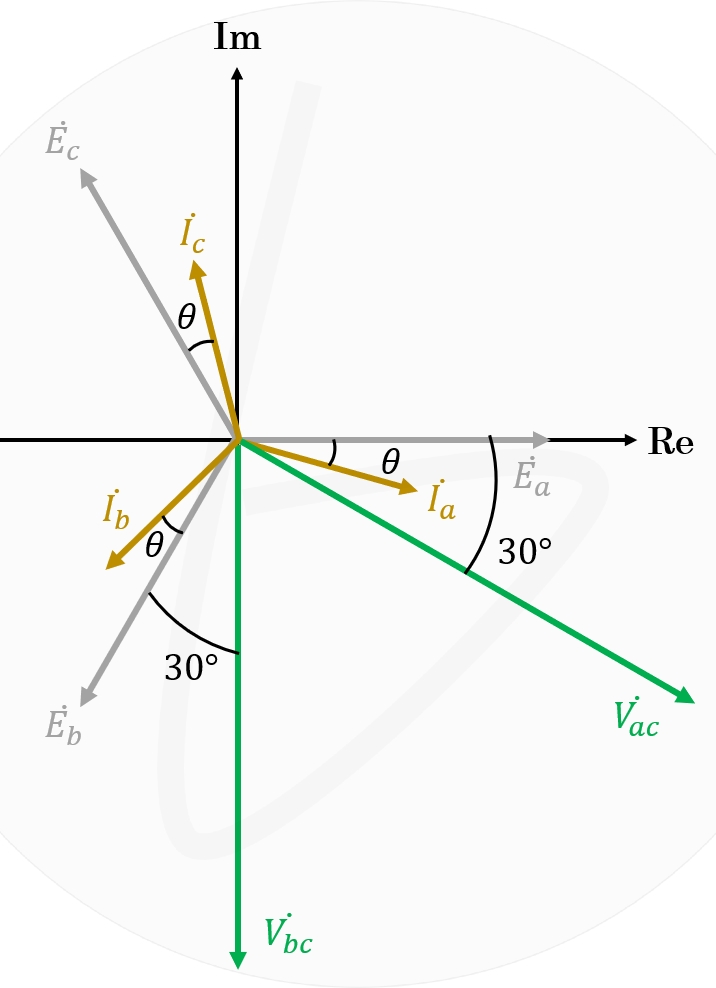
図4 2個の電力系の測定する電圧ベクトルと電流ベクトル
ここで、加法定理である、
$$\begin{cases}
cos\left(\theta-30°\right)=cos\theta cos30°+sin\theta sin30°=\frac{\sqrt{3}}{2}cos\theta+\frac{1}{2}sin\theta\\
cos\left(\theta+30°\right)=cos\theta cos30°-sin\theta sin30°=\frac{\sqrt{3}}{2}cos\theta-\frac{1}{2}sin\theta
\end{cases}$$
を利用します。
この2個の電力の和を計算すれば、
$$\begin{align}
W_1+W_2&=VIcos\left(30°-\theta\right)+VIcos\left(\theta+30°\right)\\
&=VI\left(\frac{\sqrt{3}}{2}cos\theta+\frac{1}{2}sin\theta\right)\\
&+VI\left(\frac{\sqrt{3}}{2}cos\theta-\frac{1}{2}sin\theta\right)\\
=\sqrt{3}VIcos\theta
\end{align}$$
となって、三相電力が計算できることが分かります。
これが、二電力法の原理です。
まとめ
ここまで、二電力計法によって、2個の電力計で対称三相交流回路の電力が測定できる原理について説明してきました。
この原理を知っていれば、単純に2個の電力系の指示値の足し算で、三相の電力が測定できることになります。
この問題は、電験でもよく出題されています。
例題を解いてみたい方は、令和5年度 上期 電験3種 理論 問14にチャレンジしてみてください。
以上、二電力法の原理について、参考になれば幸いです。



