この記事では、重ね合わせの理を用いた電気回路の計算について解説します。
重ね合わせの理は、普段の電気回路の計算でも頻繁に使用するほか、テブナンの定理を導出する際にも必要です。
電気回路の基本となる部分なので、確実にマスターしてください。
重ね合わせの理の計算方法
電気回路を重ね合わせで考える
重ね合わせの理では、下図のように元の回路を回路①と回路②の重ね合わせであると考えます。
 |
|
| 元の回路 | |
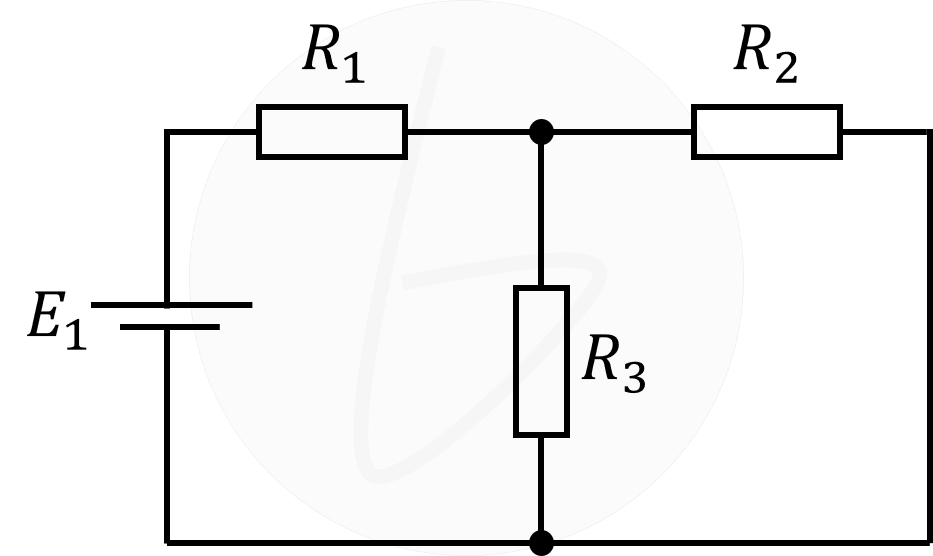 |
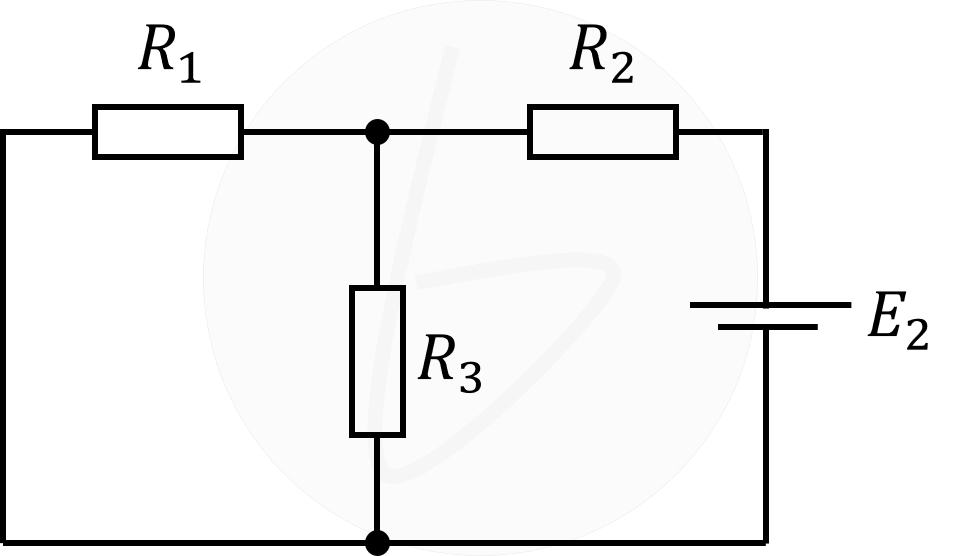 |
| 回路① | 回路② |
図1 重ね合わせの理による電気回路の分解
電圧源は短絡し電流源は開放する
重ね合わせの理によって電気回路を分解する場合、電圧源は短絡し、電流源は開放します。

図2 電圧源は短絡する
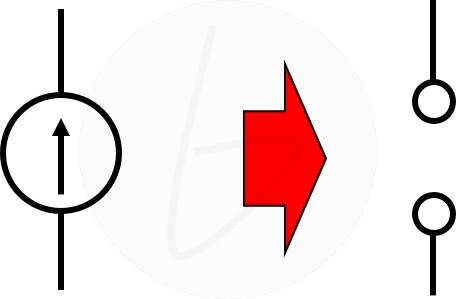
図3 電流源は開放する
例題
2個の電圧源による電気回路を重ね合わせの理で計算する
下図のように、2個の電圧源で構成された電気回路において、真ん中の抵抗$3\mathrm{Ω}$に流れる電流の大きさを計算してみます。
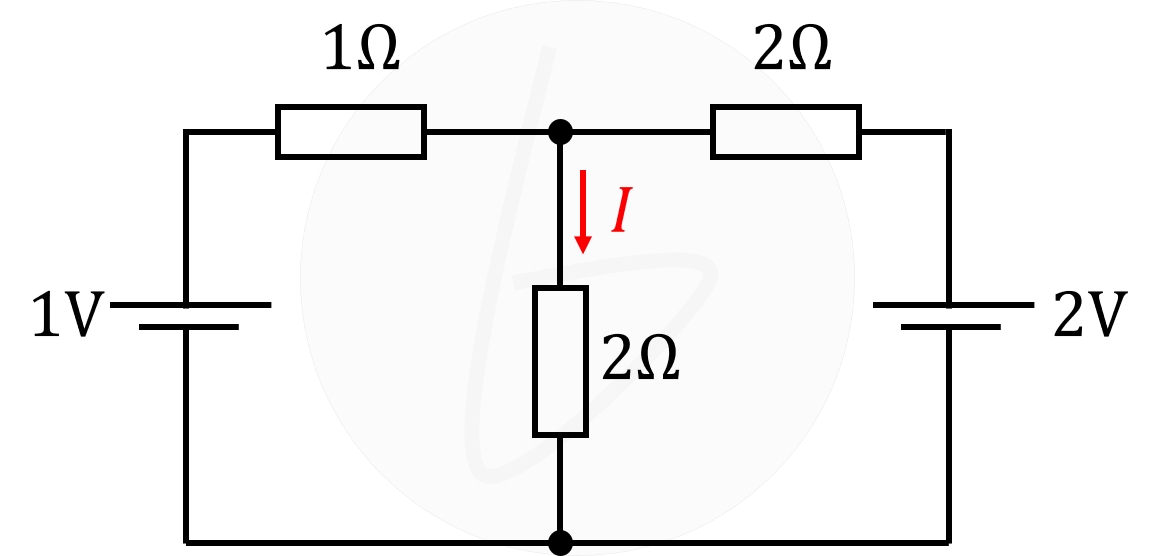
この回路は、下図の回路に分解できることが分かります。
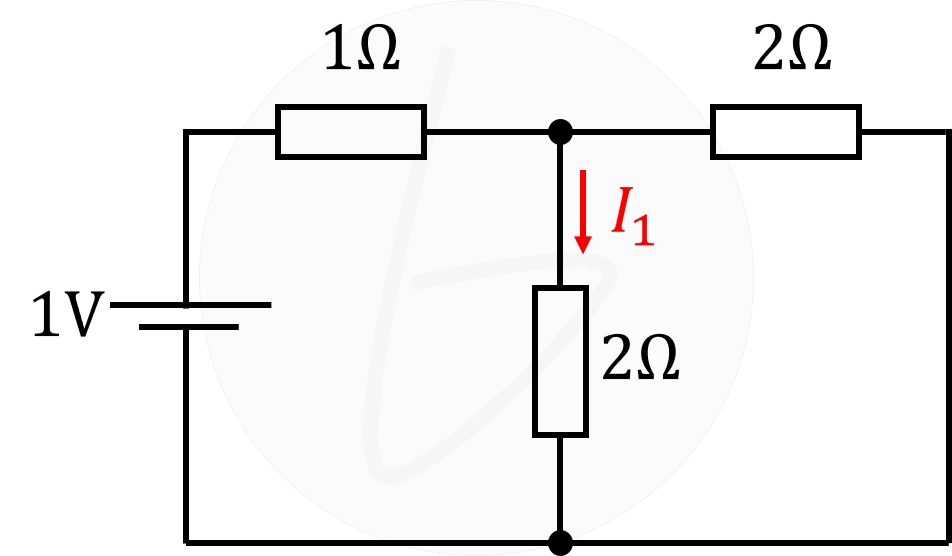 |
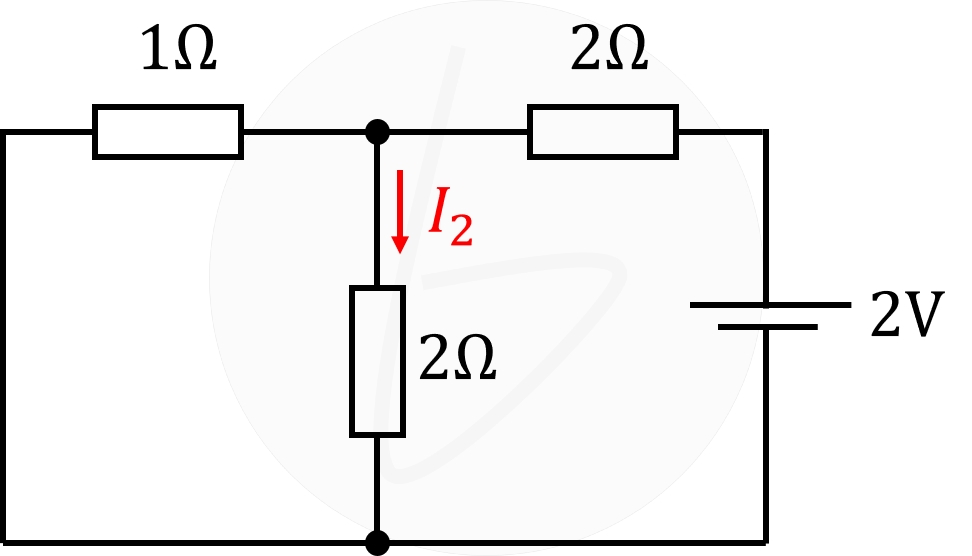 |
| 回路図① | 回路図② |
回路図①の電流$I_1$
回路図①における電流$I_1$を計算していきます。
まず、下図の通り、並列部分の合成抵抗は、
$$\frac{1}{\frac{1}{2}+\frac{1}{2}}=1\mathrm{Ω}$$
であり、回路全体の合成抵抗は、
$$1+1=2\mathrm{Ω}$$
となります。
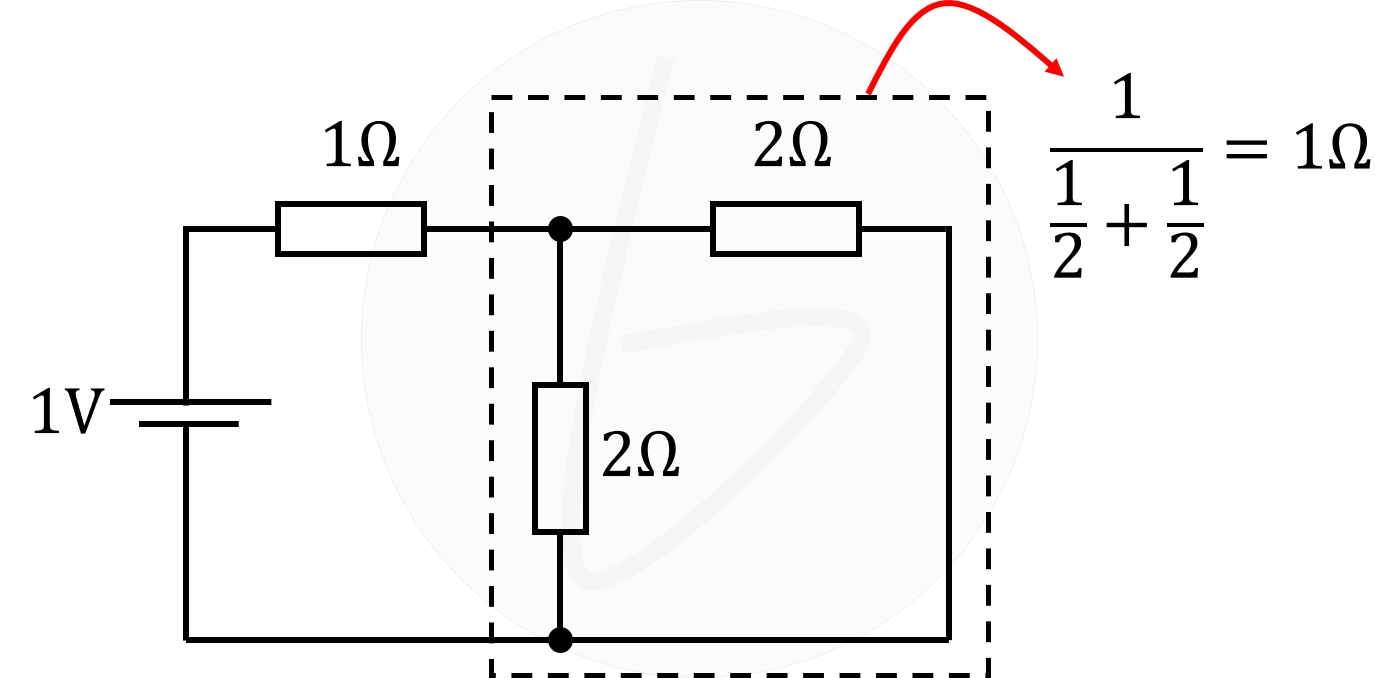
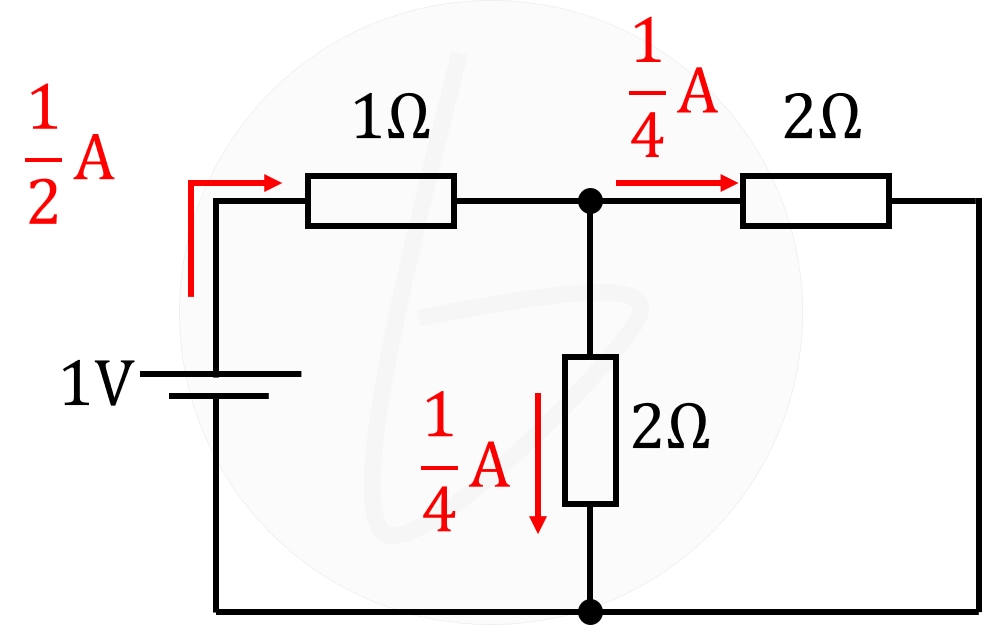
オームの法則と抵抗による電流の分流をもとに考えれば、電流は下図のように流れるので、
$$I_1=\frac{1}{4}\mathrm{A}$$
となります。
回路図②の電流$I_2$
同様に、回路図②における電流$I_2$を計算していきます。
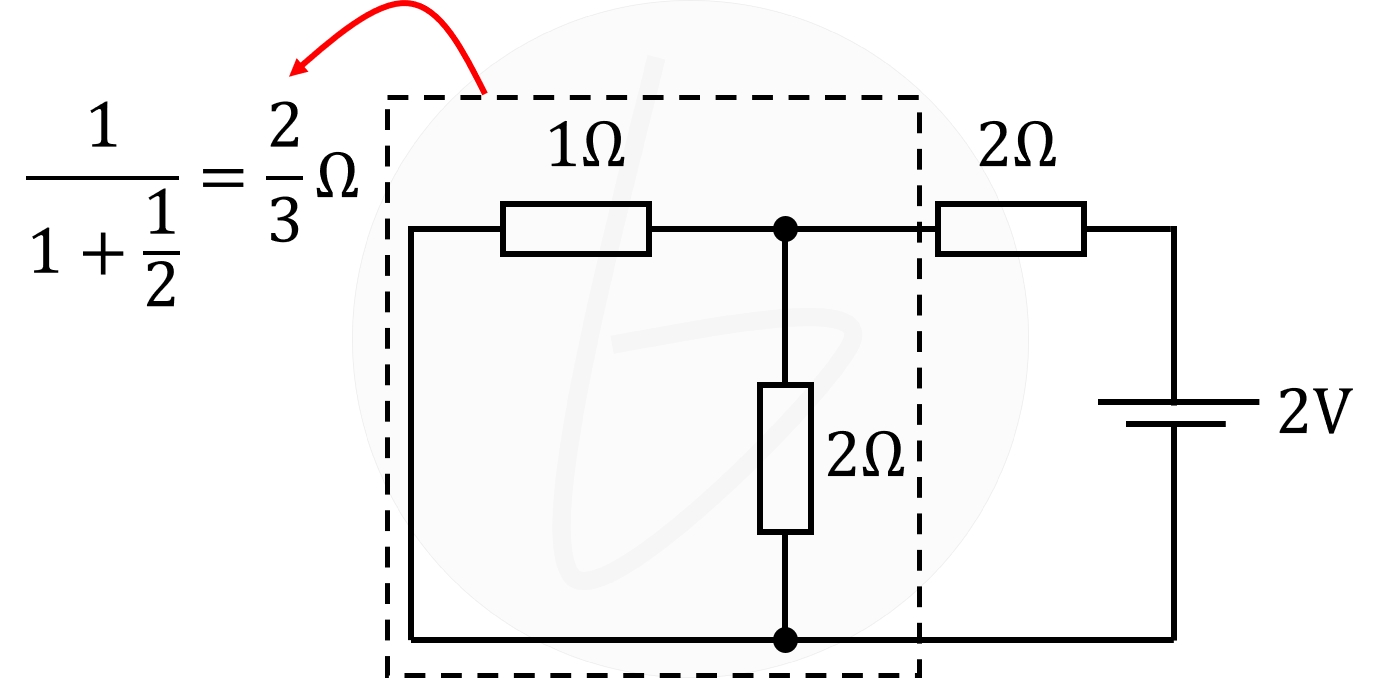
下図の通り、並列部分の合成抵抗は、
$$\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\mathrm{Ω}$$
であり、回路全体の合成抵抗は、
$$2+\frac{2}{3}=\frac{8}{3}\mathrm{Ω}$$
となります。
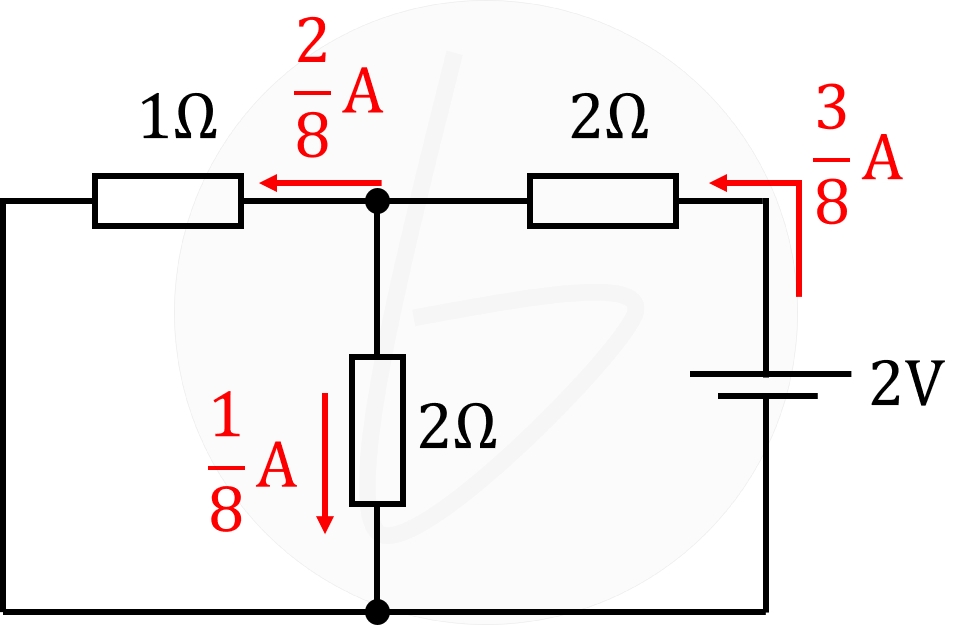
オームの法則と抵抗による電流の分流をもとに考えれば、電流は下図のように流れるので、
$$I_2=\frac{1}{8}\mathrm{A}$$
となります。
回路電流$I$を計算する
重ね合わせの理より、
$$I=I_1+I_2=\frac{1}{4}+\frac{1}{8}=\frac{3}{8}\mathrm{A}$$
と計算できました。
電圧源と電流源を含む電気回路を重ね合わせの理で計算する
2個目の例として、電圧源に加えて、電流源を含む場合を考えてみましょう。
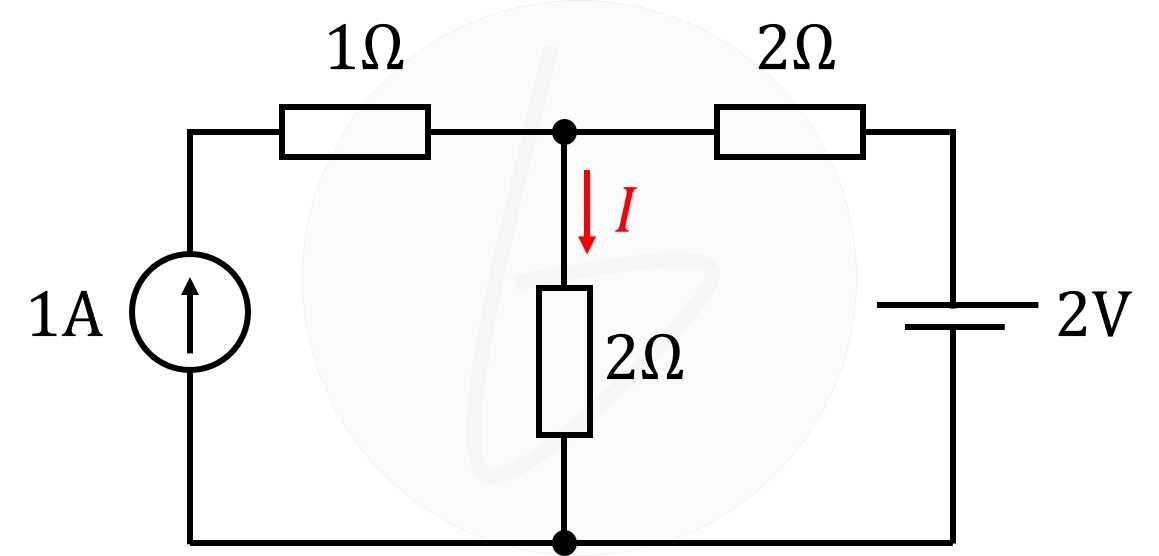
この回路は、重ね合わせの理によって、下図のように分解できます。
電流源は開放することに注意してください。
 |
 |
| 回路図① | 回路図② |
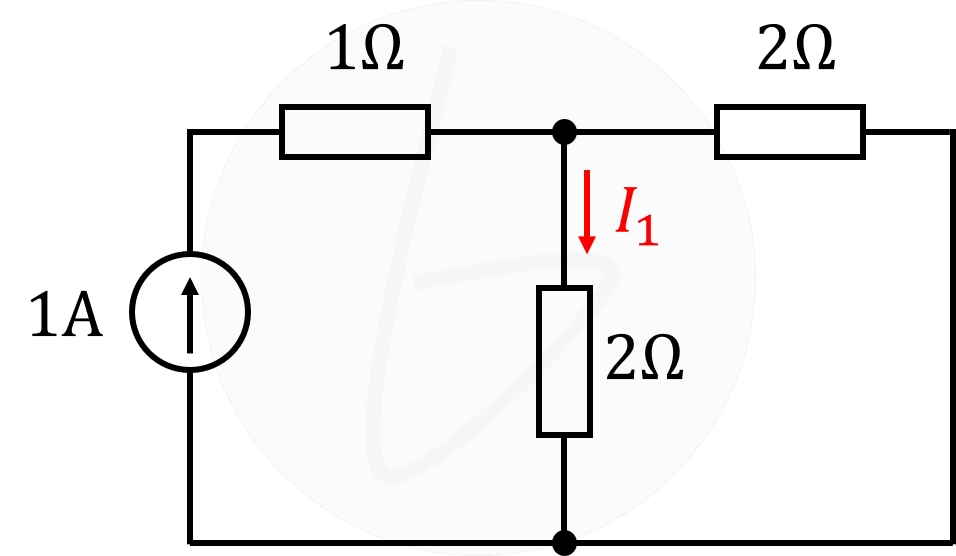
回路図①の電流$I_1$
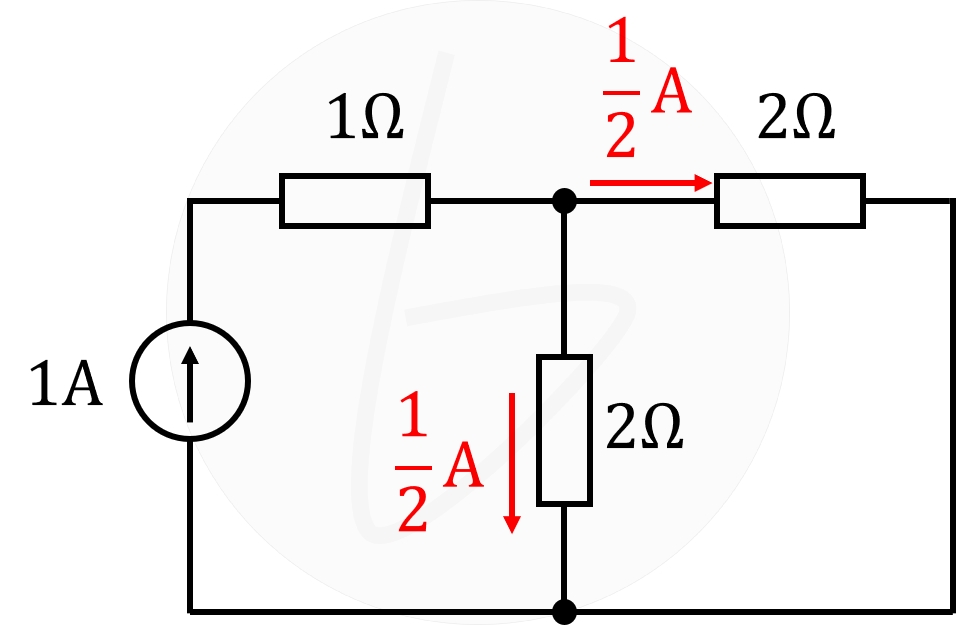
回路図①の電流$I_1$を計算すれば、$1\mathrm{A}$の電流が2個の$2\mathrm{Ω}$の抵抗で分流するので、
$$I_1=\frac{1}{2}\mathrm{A}$$
であるとわかります。
回路図②の電流$I_2$
次に、回路図②の電流$I_2$は、電流源が開放されているので、単に$2\mathrm{Ω}$の抵抗の直列接続になります。
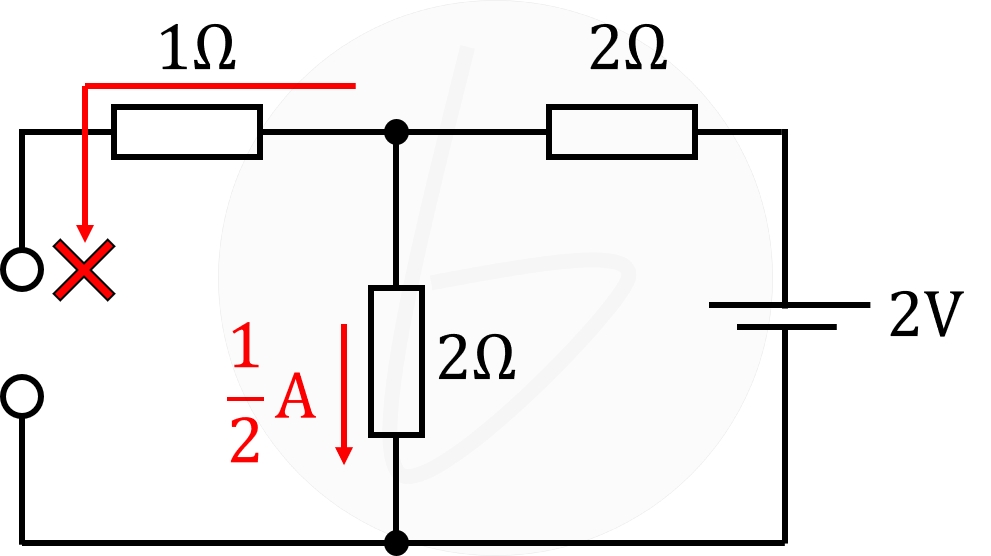
よって、
$$I_2=\frac{2}{2+2}=\frac{1}{2}\mathrm{A}$$
であると計算できます。
回路電流$I$を計算する
重ね合わせの理より、
$$I=I_1+I_2=\frac{1}{2}+\frac{1}{2}=1\mathrm{A}$$
と計算できました。
まとめ
ここまで、重ね合わせの理の解説と、例題によって具体的な計算手法を説明してきました。
重ね合わせの理が理解できれば、テブナンの定理が導出できます。
テブナンの定理は、複雑な回路を計算するときに強力な計算ツールとなります。
回路計算スキルの向上のために、テブナンの定理の導出と使い方も併せて確認しておいてください。
以上、重ね合わせの理による回路計算について、参考になれば幸いです。




