この記事では、電気回路で基本的な法則となる、オームの法則とキルヒホッフの法則について解説していきます。
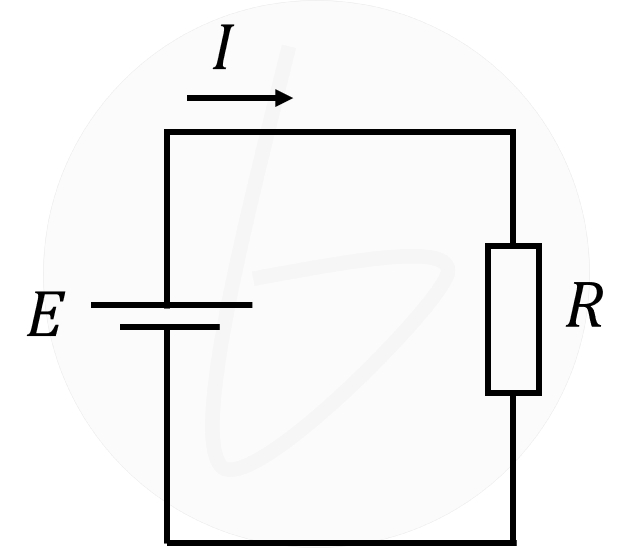
下図の回路を例にして、オームの法則とキルヒホッフの法則で合成抵抗を求めていきましょう。
オームの法則
オームの法則とキルヒホッフの法則は、直流回路だけではなく、交流回路でも成り立つ電気回路の基本公式です。
オームの法則
電圧$V\left[\mathrm{V}\right]$、電流$I\left[\mathrm{A}\right]$、抵抗$R\left[\mathrm{\Omega}\right]$とすると、
$$V=RI$$
の関係があり、これをオームの法則といいます。
オームの法則の覚え方
オームの法則の覚え方として、下図があります。

この図の意味は、求めたいものを隠せば、オームの法則が成立するという意味で、たとえば下図の通り、$V\left[\mathrm{V}\right]$、$I\left[\mathrm{A}\right]$、$R\left[\mathrm{\Omega}\right]$が求められます。
 |
 |
 |
| $V=IR$ | $I=\frac{V}{R}$ | $R=\frac{V}{I}$ |
キルヒホッフの法則
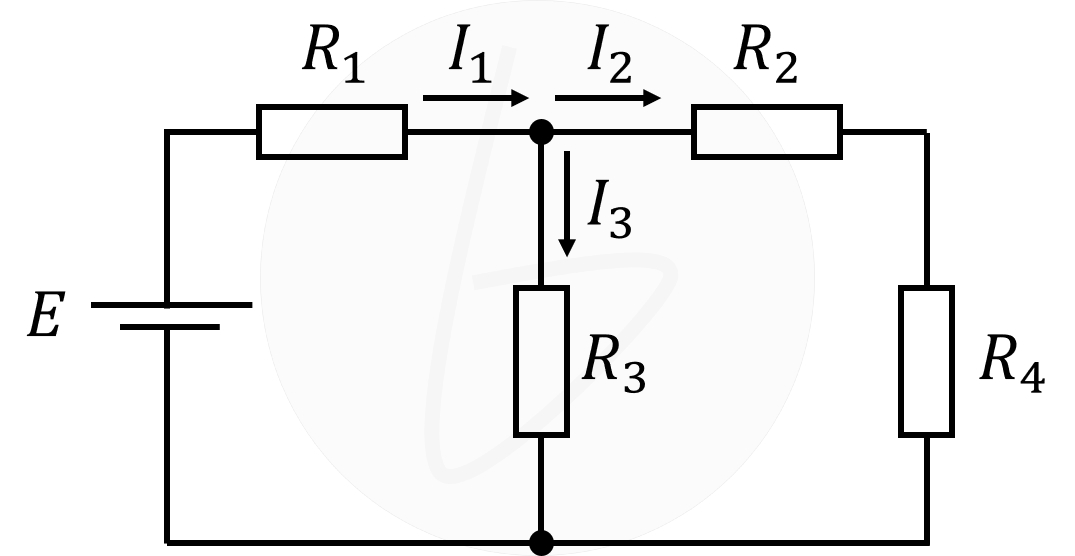
キルヒホッフの法則を考えていくうえで、例題として以下の回路を考えていきます。
この回路において、各部の電流$I_1$、$I_2$、$I_3$および電源から見た合成抵抗$R$を計算してみましょう。
キルヒホッフの第1法則
ある点において、流入する電流の総和と流出する電流の総和は等しいことを示す法則です。
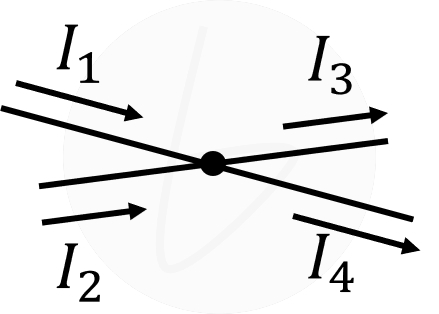
下図のように、ある点に対して電流$I_1$、$I_2$が流入し、$I_3$、$I_4$が流出している場合、
$$I_1+I_2=I_3+I_4$$
が成り立ちます。
キルヒホッフの第1法則は、水の流れに例えれば非常に簡単です。
上の図において、電流を水と考えれば、水は途中で消滅しないので、分岐・合流点に流入した量と流出した量は等しいはずです。
水と同じように、電流も途中で消滅しないので、キルヒホッフの第1法則が成り立つことが分かります。
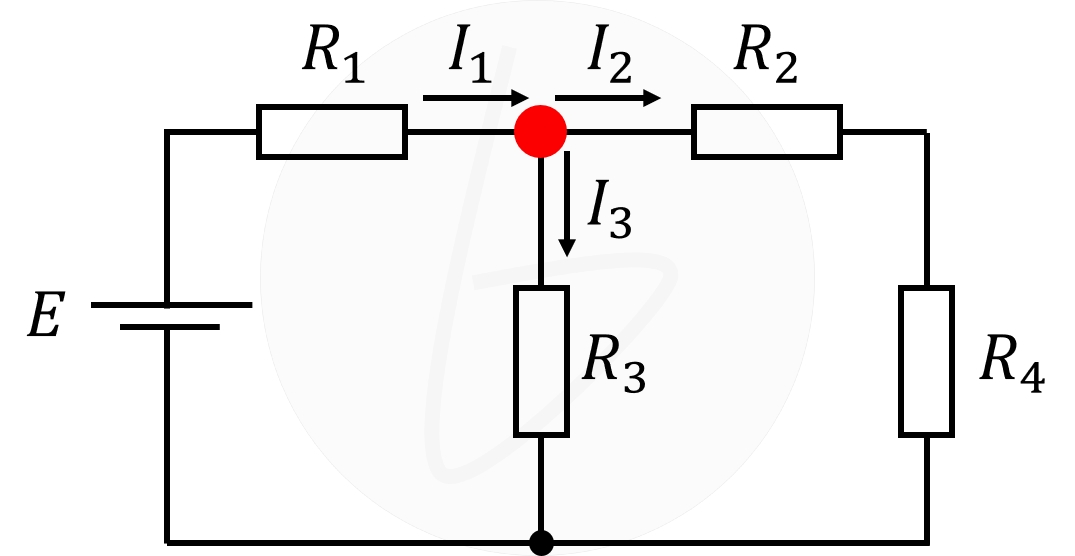
では、冒頭の回路図で、赤丸で示した部分について、キルヒホッフの第1法則を適用すれば、
$$I_1=I_2+I_3$$
という方程式が立式できることが分かります。
キルヒホッフの第2法則
ある閉回路を1周したとき、起電力の総和と電圧降下の総和は等しいことを示す法則です。
題材としている以下の回路において、抵抗で生じている電圧降下を図示すれば、以下の通りになります。
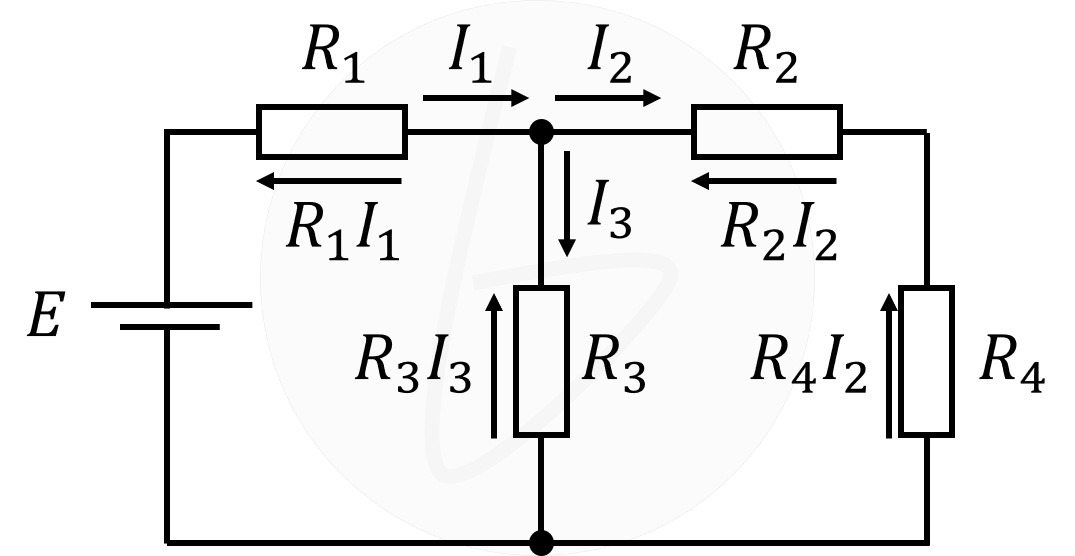
ここで、①および②で示される閉回路を考え、ここにキルヒホッフの第2法則を適用すれば、
$$\left\{\begin{matrix}
E=R_1I_1+R_3I_3\\
0=R_2I_2+R_4I_2-R_3I_3
\end{matrix}\right.$$
となることが分かります。
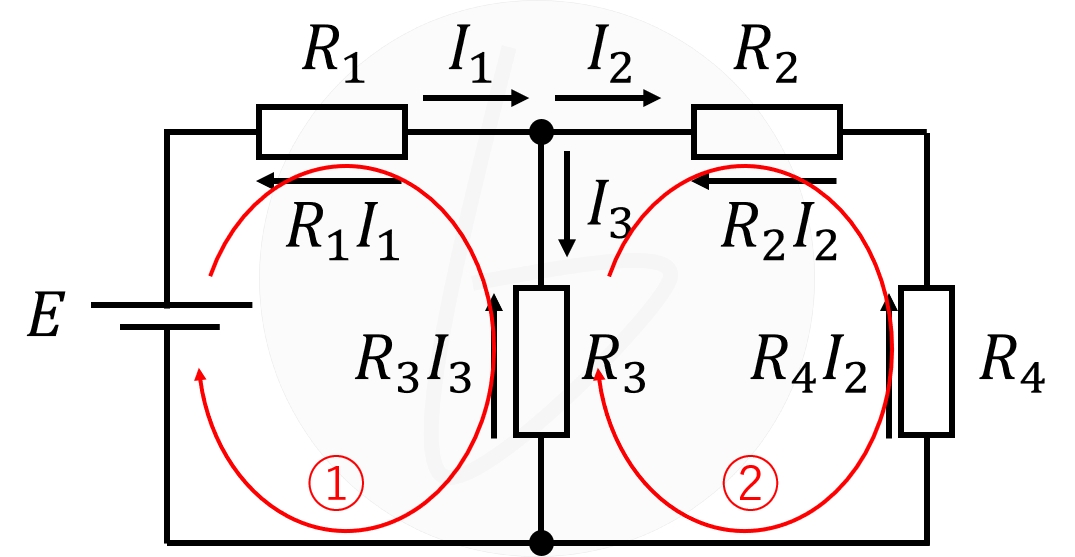
キルヒホッフの法則のまとめ
キルヒホッフの第1法則、キルヒホッフの第2法則から、
$$\left\{\begin{matrix}
I_1=I_2+I_3\\
E=R_1I_1+R_3I_3\\
0=R_2I_2+R_4I_2-R_3I_3
\end{matrix}\right.$$
が導けたので、これを解けば、
$$\begin{cases}
I_1=\frac{R_2+R_3+R_4}{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_3R_4}E\\
I_2=\frac{R_2+R_4}{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_3R_4}E\\
I_1=\frac{R_3}{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_3R_4}E
\end{cases}$$
となります。
ここで、電源から見た合成抵抗$R$は、
$$R=\frac{E}{I_1}=\frac{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_3R_4}{R_2+R_3+R_4}$$
となることが分かります。
参考に、抵抗の直並列接続なので、
$$R=R_1+\frac{1}{\frac{1}{R_2+R_4}+\frac{1}{R_3}}=R_1+\frac{R_2R_3+R_3R_4}{R_2+R_3+R_4}=\frac{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_3R_4}{R_2+R_3+R_4}$$
となって、結果が一致することが分かります。
【例題】オームの法則とキルヒホッフの法則
ではもう一問、オームの法則とキルヒホッフの法則を使う計算問題の例題を紹介します。
問題
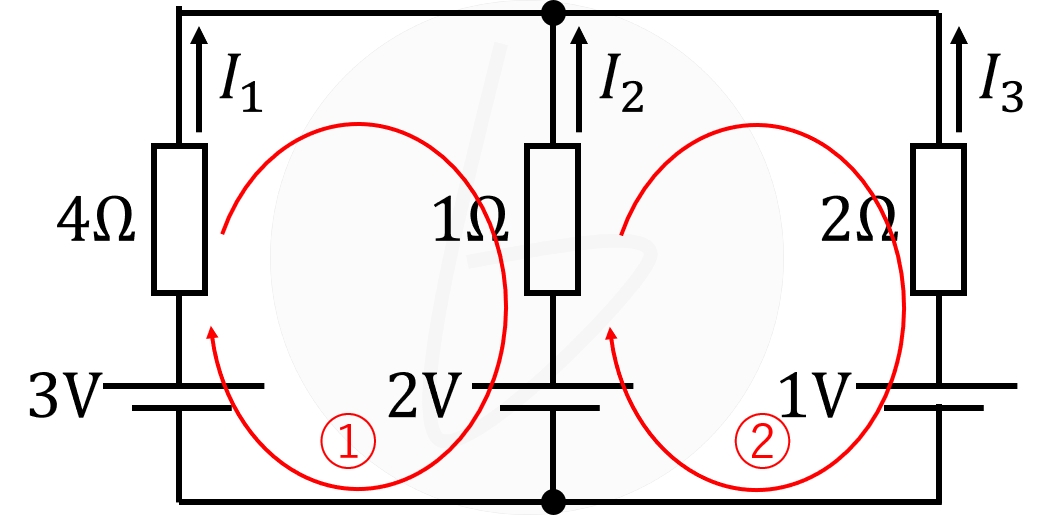
下図に示す回路において、電流$I_1$、$I_2$、$I_3$を求めてみましょう。
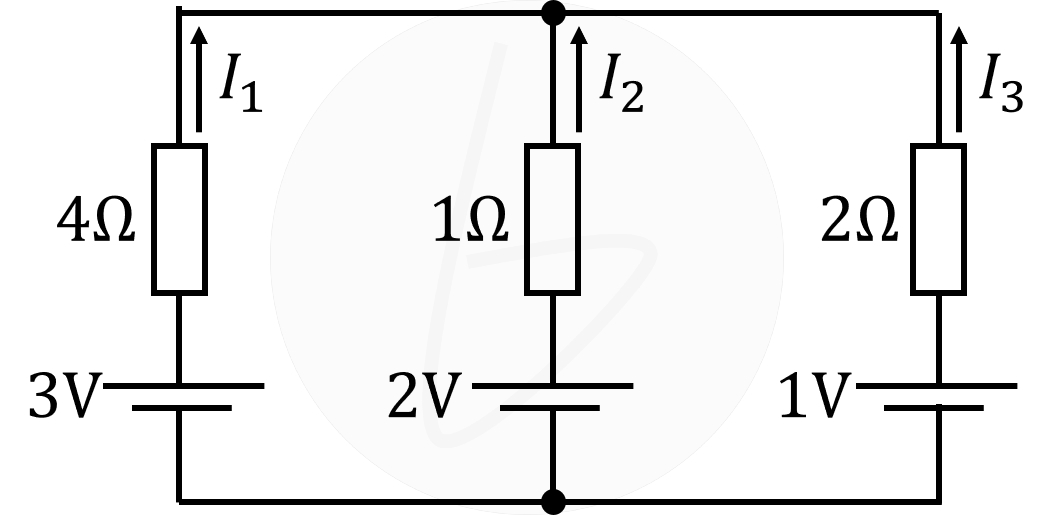
解答
下図に示す赤丸の位置において、キルヒホッフの第1法則を使えば、
$$I_1+I_2+I_3=0$$
となります。
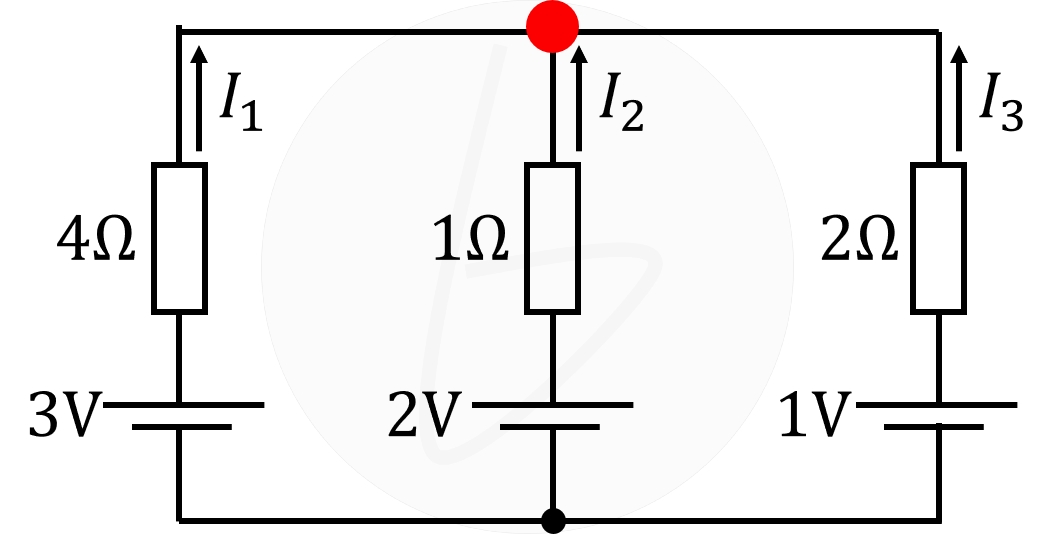
次に、下図に示す閉回路①と②を考えれば、キルヒホッフの第2法則から、
$$\begin{cases}
3-2=4I_1-I_2\\
2-1=I_2-2I_3
\end{cases}$$
となります。
これらを連立すれば、
$$\begin{cases}
I_1+I_2+I_3=0\\
3-2=4I_1-I_2\\
2-1=I_2-2I_3
\end{cases}$$
となるので、これを解けば、
$$\begin{cases}
I_1=\frac{2}{7}\left[\mathrm{A}\right]\\
I_2=\frac{1}{7}\left[\mathrm{A}\right]\\
I_3=-\frac{3}{7}\left[\mathrm{A}\right]
\end{cases}$$
となります。




