みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、電磁気学の基礎である
- 点電荷の作る電界
- クーロンの法則
について説明します。
点電荷の作る電界については、本来はガウスの法則を点電荷に適用した場合に導かれる計算結果なのですが、電磁気学の最初は暗記事項とされることも多いです。
導出などが気になる方は、ガウスの法則の記事をご覧ください。
参考に、物理学における力はほぼすべてが接触した状態で働きます。
なので、物理における問題で複雑な機構があっても、基本的には全てその機構に直接接触しているものから伝わる力を考慮すればいいです。
非接触、すなわち遠隔的に働く力はたったの4つしかなく、
- 重力(広義で万有引力)
- クーロン力
- 強い力
- 弱い力
です。
その内の1つであるクーロン力について学んでいきます。
※このうち、強い力、弱い力は原子物理学なので、通常は考慮しません。
点電荷の作る電界とクーロンの法則の公式
点電荷の作る電界の公式
ある点電荷$Q$[C]があったとすれば、その点電荷から$r$[m]離れた位置に生じる電界$E$は、
$$E=\frac{Q}{4\pi \epsilon_0 r^2}{\rm [V/m]} \tag{1}$$
となります。
ただし、電気力線の方向は、図1に示す通り、$Q$の符号が、
- 正のとき離れる方向
- 負のとき近づく方向
になります。
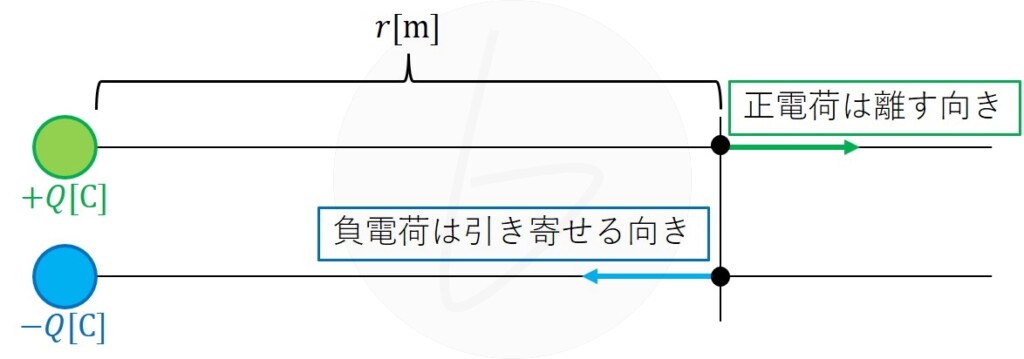
図1 正電荷と負電荷の作る電界の向き
クーロン力の公式(点電荷の間に働く静電力)
また、その場所に$q$[C]の点電荷があるとすれば、その点電荷に生じる電磁力$F$[N]は、
$$F=qE{\rm [N]}\tag{2}$$
となります。
ただし、$Q$と$q$が、
- 同符号のとき:斥力
- 異符号のとき:引力
となります。
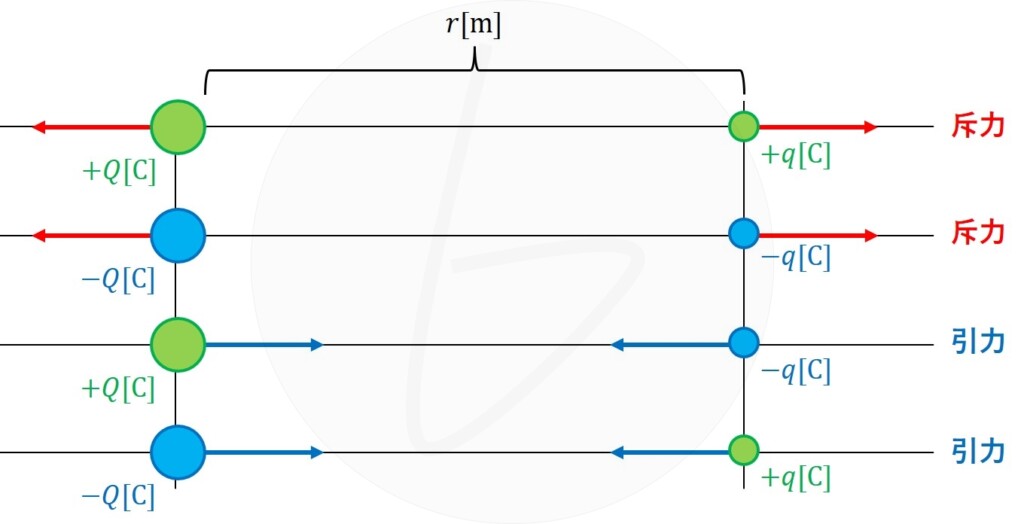
図2 電荷の符号による斥力と引力の関係
参考に、$Q$[C]の点電荷に働くクーロン力と、$q$[C]の点電荷に働くクーロン力は同じです。
$Q$[C]の点電荷が$q$[C]の点電荷の位置に生じさせる電界を$E_Q$とすれば、
$$E_Q=\frac{Q}{4\pi \epsilon_0 r^2}$$
となるので、$q$[C]の点電荷に働くクーロン力$F_q$は、
$$F_q=qE_Q=\frac{qQ}{4\pi \epsilon_0 r^2}$$
となります。
一方、$q$[C]の点電荷が$Q$[C]の点電荷の位置に生じさせる電界を$E_q$とすれば、
$$E_q=\frac{q}{4\pi \epsilon_0 r^2}$$
となるので、$Q$[C]の点電荷に働くクーロン力$F_Q$は、
$$F_Q=QE_q=\frac{qQ}{4\pi \epsilon_0 r^2}$$
となり、
$$F_q=F_Q$$
になります。
クーロン力のベクトル計算の例題
クーロン力は力であり、方向を持つベクトル量です。
そのため、複数の点電荷が存在する場合には、斥力や引力のベクトル合成した結果が答えになります。
では、3つの点電荷が存在する問題について、例題を見ていきましょう。
例題
図に示す通り、1辺の長さ$r$[m]である正三角形の頂点に点電荷A、B、Cが存在している。
この時、
- 点電荷Bが点電荷Aに及ぼす力の大きさ$|\boldsymbol{F_{AB}}|$
- 点電荷Cが点電荷Aに及ぼす力の大きさ$|\boldsymbol{F_{CA}}|$
を求め、点電荷Aに働く力のベクトル$\boldsymbol{F_A}=\boldsymbol{F_{AB}}+\boldsymbol{F_{CA}}$を図示せよ。
また、$|\boldsymbol{F_{CA}}|$の大きさを求めよ。
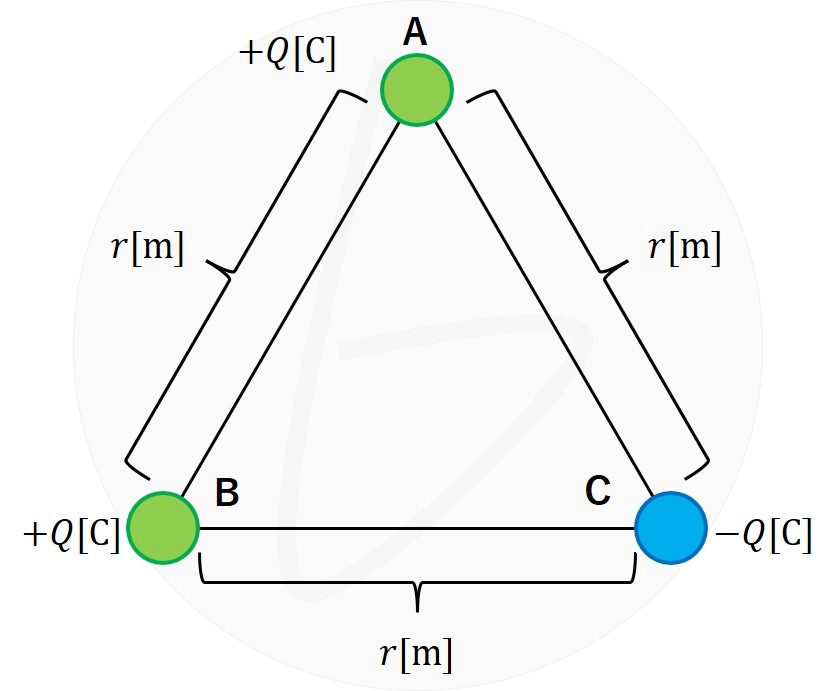
問題図
回答
電荷の符号を見れば、
- A:$+Q$[C]
- B:$+Q$[C]
- C:$-Q$[C]
であるので、AB間は同符号の電荷なので斥力が、AC間は異符号の電荷なので引力が働く。
また、点電荷のB点とC点に存在する点電荷の大きさは$Q$[C]で等しいので、点電荷Bが及ぼすクーロン力$\boldsymbol{F_{AB}}$と点電荷Cが及ぼすクーロン力$\boldsymbol{F_{CA}}$の大きさは等しく、
$$|\boldsymbol{F_{AB}}|=|\boldsymbol{F_{CA}}|=\frac{Q^2}{4\pi \epsilon_0 r^2}\tag{解1}$$
と計算できる。
その結果、解図1のようなクーロン力が生じている。
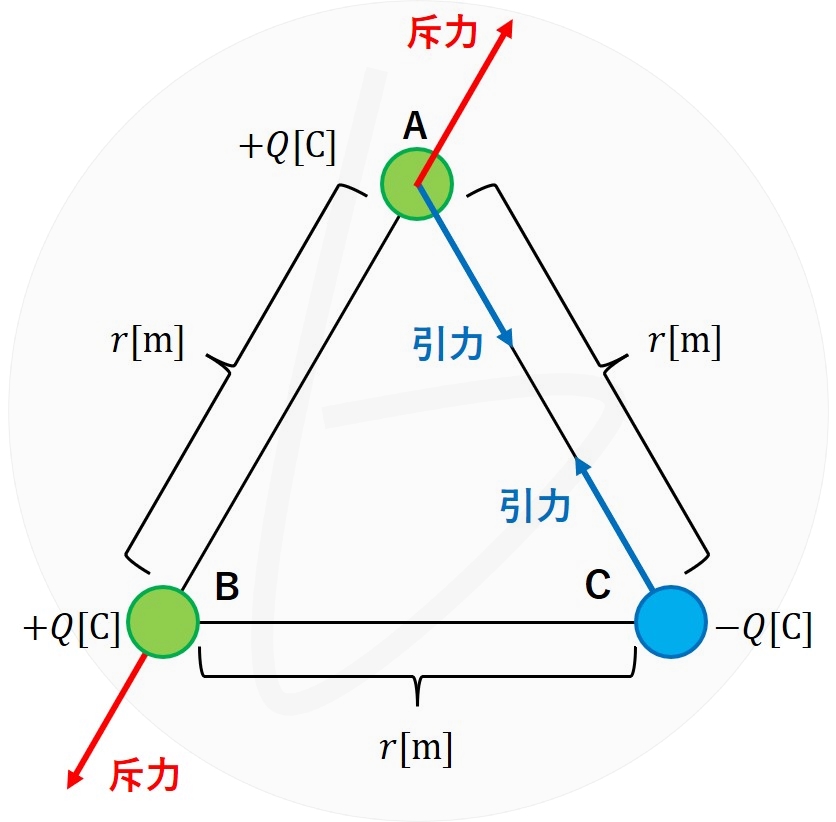
解図1
点電荷Aに働く力$\boldsymbol{F_A}$は、$\boldsymbol{F_{AB}}$と$\boldsymbol{F_{CA}}$のベクトル和なので、解図2の通りになる。
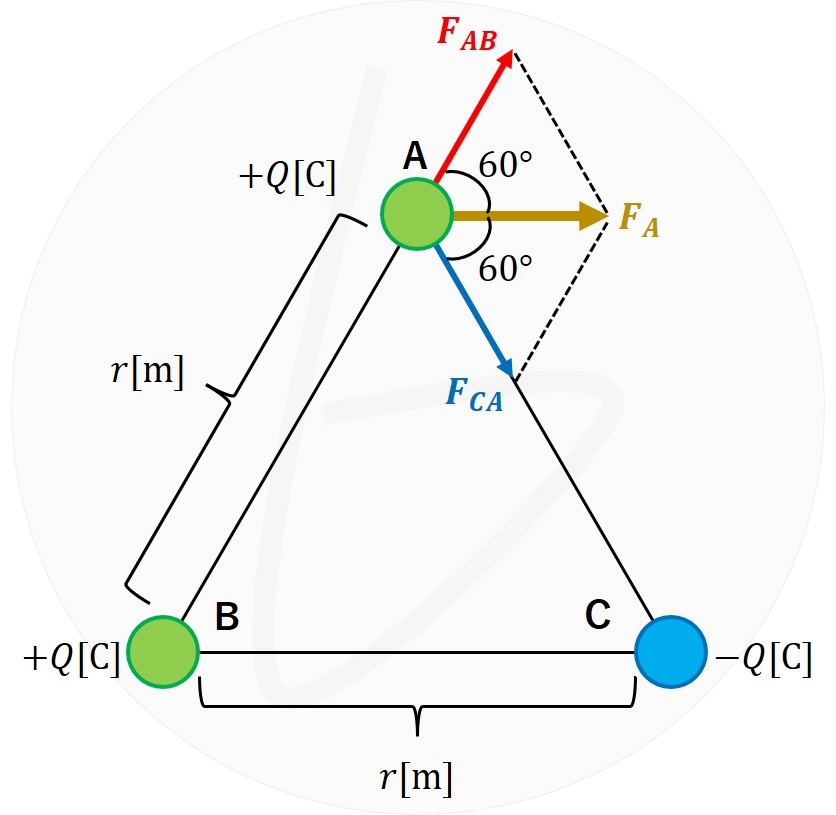
解図2
$\boldsymbol{F_A}$の大きさを計算する。
解図2で示す通り、ベクトル合成の結果、画面縦方向の力は打ち消され、画面右向きの力のみが残るので、
$$\begin{align}
\left |\boldsymbol{F_A}\right |&=\left |\boldsymbol{F_{AB}} \right |cos60°+\left |\boldsymbol{F_{CA}}\right |cos60°\\
&=\frac{Q^2}{4\pi \epsilon_0 r^2}・\frac{1}{2}+\frac{Q^2}{4\pi \epsilon_0 r^2}・\frac{1}{2}\\
&=\frac{Q^2}{4\pi \epsilon_0 r^2}\tag{解2}
\end{align}
$$
となる。
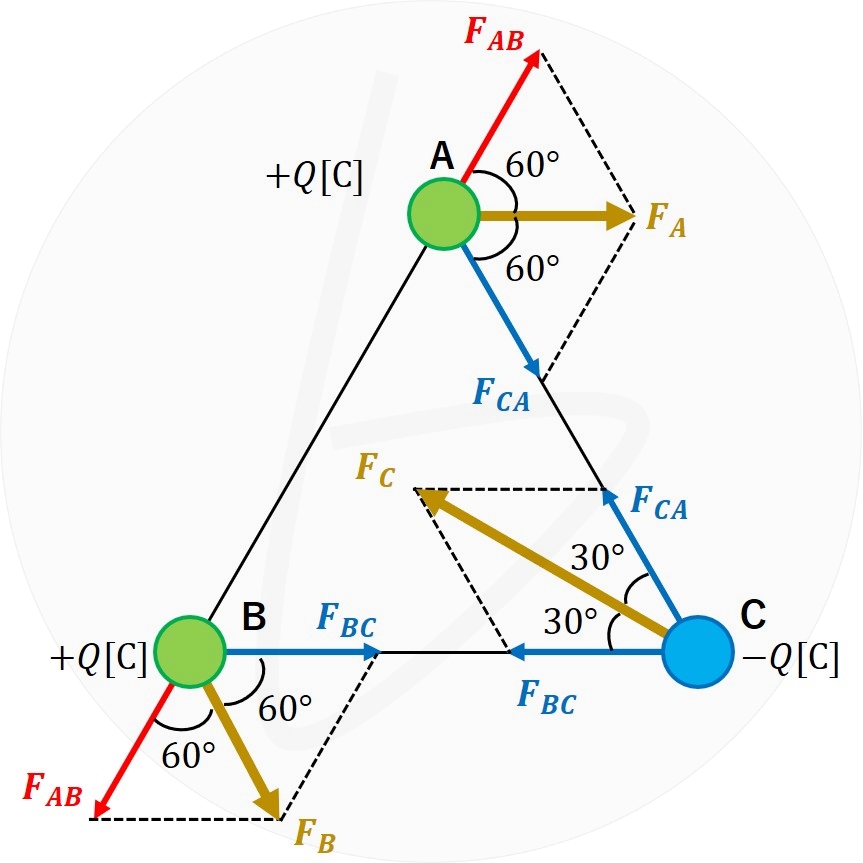
参考に、それぞれ点電荷に働くクーロン力をすべて図示すれば、下の図のようになります。
- $\boldsymbol{F_A}$:点電荷Aに働くクーロン力
- $\boldsymbol{F_B}$:点電荷Bに働くクーロン力
- $\boldsymbol{F_C}$:点電荷Cに働くクーロン力
まとめ
ここまで、電磁気学の最初の第一歩であるクーロンの法則について説明してきました。
$$E=\frac{Q}{4\pi \epsilon_0 r^2}$$
$$F=qE$$
だけ知っていれば、あとは力学的にベクトルの計算だけでクーロン力が求まります。
クーロン力は、点電荷にガウスの法則を適用すれば求まるので、導出方法も併せて知っておいてください。
以上、クーロンの法則について参考になれば幸いです。