みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
今回は、同期電動機の出力について導出していきます。
同期電動機は、同期発電機に電圧を印加することでモータとして動作させるものです。
ベクトル図も基本的には同じなので、同期発電機の出力式と関連付けて理解するといいでしょう。
▼おすすめ記事▼
同期電動機の出力式
一般式
同期電動機の1相当たりの機械出力は、
$$P=\frac{E_0V}{Z_s}cos(\alpha-\delta) -\frac{V^2}{Z_s}cos\alpha \tag{1}$$
となります。
ただし、
- $V$:端子電圧(外部電源電圧)
- $E_0$:速度誘起電力(逆起電力)
- $Z_s=\sqrt{r_a+jx_s}$:同期インピーダンス
- $\alpha$:インピーダンス角
- $\delta$:負荷角(内部相差角)
となります。
速度誘起電力(逆起電力)$V$は、同期発電機の場合には無負荷誘導起電力になり、意味するものは全く同じです。
そもそも、無負荷誘導起電力は同期発電機に界磁を与えて、外部からの機械的回転力によって同期機を回転させるときに生じる起電力のことです。
同期電動機で使用した場合は、界磁を与え、外部電源によって駆動する時の逆起電力です。
キーワードとして、「界磁電流があるときに回転したとき生じる起電力」となるので、
- 速度誘起電力(逆起電力)
- 無負荷誘導起電力
は、物理現象として全く同じです。
巻線抵抗を無視する場合
巻線抵抗を無視し$r_a<<x_s$とする場合、$Z_s≒x_s$とできて、またインピーダンス角$\alpha=\frac{\pi}{2}$となるので、式(1)は、
$$P=\frac{E_0V}{x_s}sin\delta \tag{2}$$
となる。
ここで最高出力は$sin\delta=1$のときであり、すなわち負荷角$\delta=\frac{\pi}{2}$のときである。
同期電動機の等価回路とベクトル図
同期発電機の等価回路を図1に示します。
同期発電機のときは、同期機そのものがエネルギーを供給する交流電源となっていましたが、電動機で使用する場合には、速度に応じた逆起電力を生じる交流電源となり、逆起電力に打ち勝つ外部電源電圧によって電流を流しトルクを生み出す、全く逆の動作をさせます。
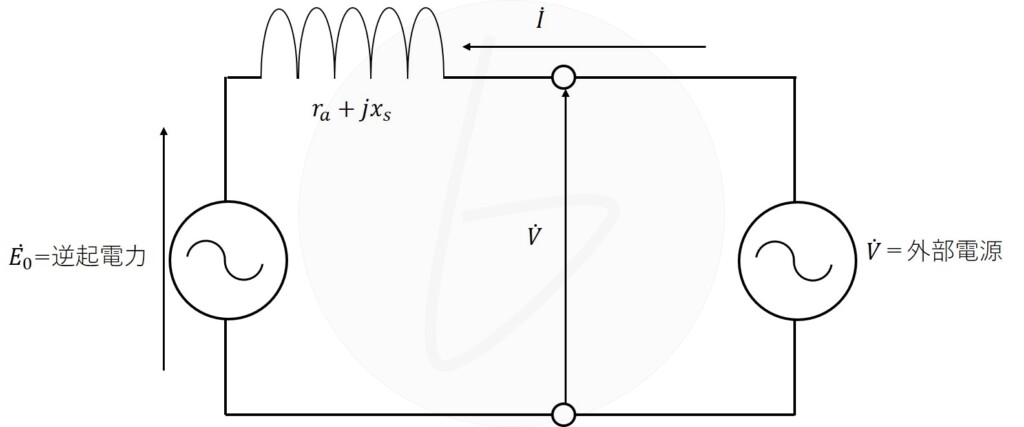
図1 同期電動機の等価回路
ちょっとややこしいかもしれませんが、同期電動機内部の電源では、電源に向かって電流が流入する形になるので、エネルギーを消費します。
流入したエネルギーである、
$$P=Re\left[\dot{E_0}{\dot{I}}\right]$$
が機械的出力となります。
もし、上記の現象を電気的に理解するとすれば、電源にエネルギーを返す回生動作に近いかもしれません。
同期発電機のベクトル図を図2に示します。
等価回路が分かれば、同期電動機のベクトル図は簡単に描けると思います。
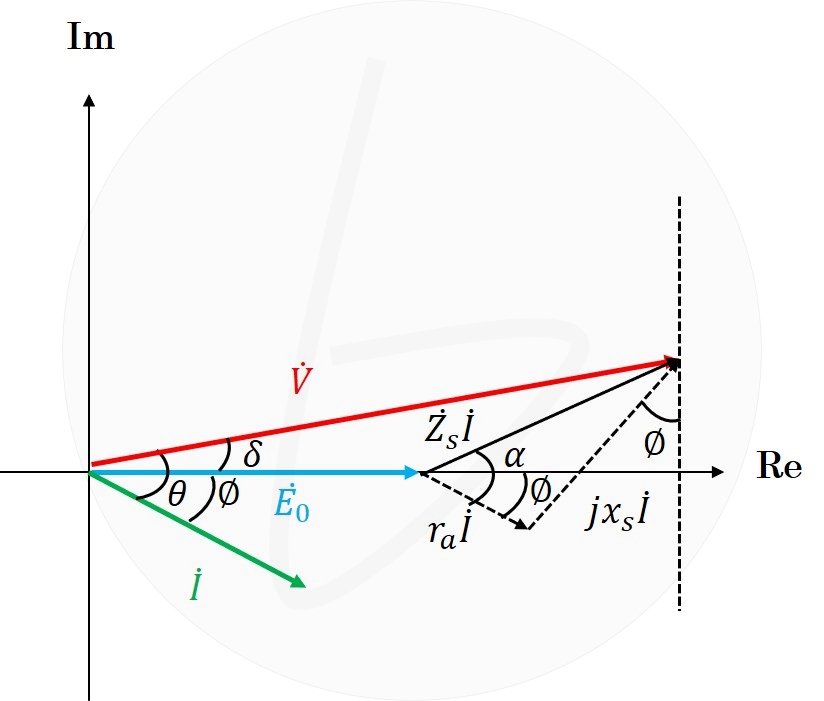
図2 同期電動機のベクトル図
同期電動機の機械的出力の導出
同期電動機の1相の出力は、
$$P=E_0Icos\phi \tag{3}$$
で示せます。
同期電動機や直流電動機は、逆起電力×電流(×逆起電力部の力率:同期電動機の場合のみ)で計算できることを知っておくと便利です。
同期電動機の場合、端子部分では力率$con\theta$ですが、逆起電力部分の力率は$cos\phi$です。
先ほども書きましたが、同期機の発電機部分に流入するエネルギーが機械出力なので、内部の力率は内部相差角そのものになるのです。
実軸について
同期電動機の実軸成分について記したベクトル図を図3に示します。
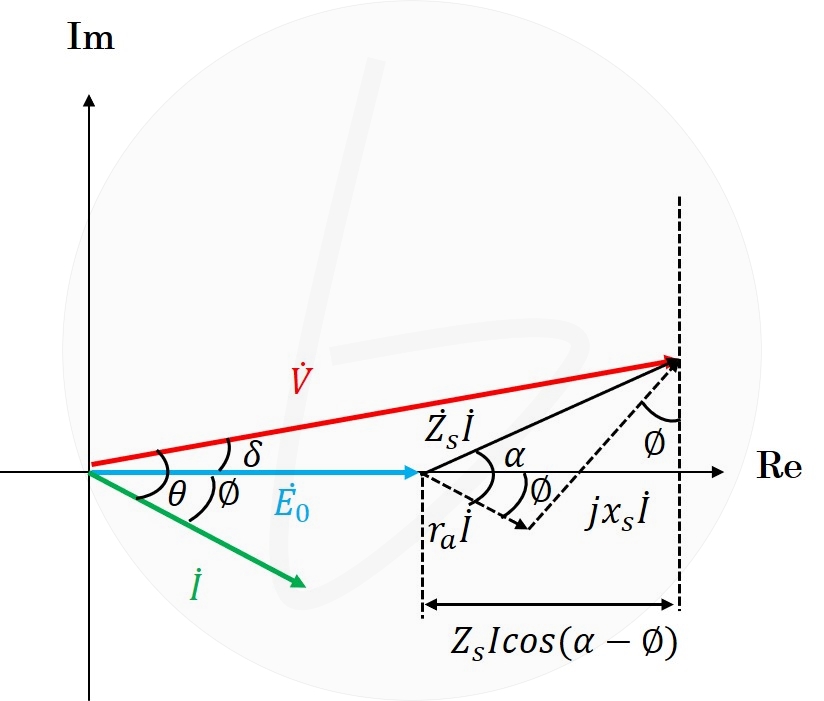
図3 同期電動機のベクトル図(実軸成分の計算)
$$E_0+Z_sIcos(\alpha-\phi)=Vcos\delta \tag{4}$$
加法定理で展開して、
$$E_0+Z_sIcos\alpha cos\phi+Z_sIsin\alpha sin\phi =Vcos\delta \tag{5}$$
$cos\alpha$をかけて、
$$E_0cos\alpha+Z_sIcos^2\alpha cos\phi+Z_sIsin\alpha cos\alpha sin\phi =Vcos\alpha cos\delta \tag{6}$$
虚軸について
同期電動機の実軸成分について記したベクトル図を図4に示します。
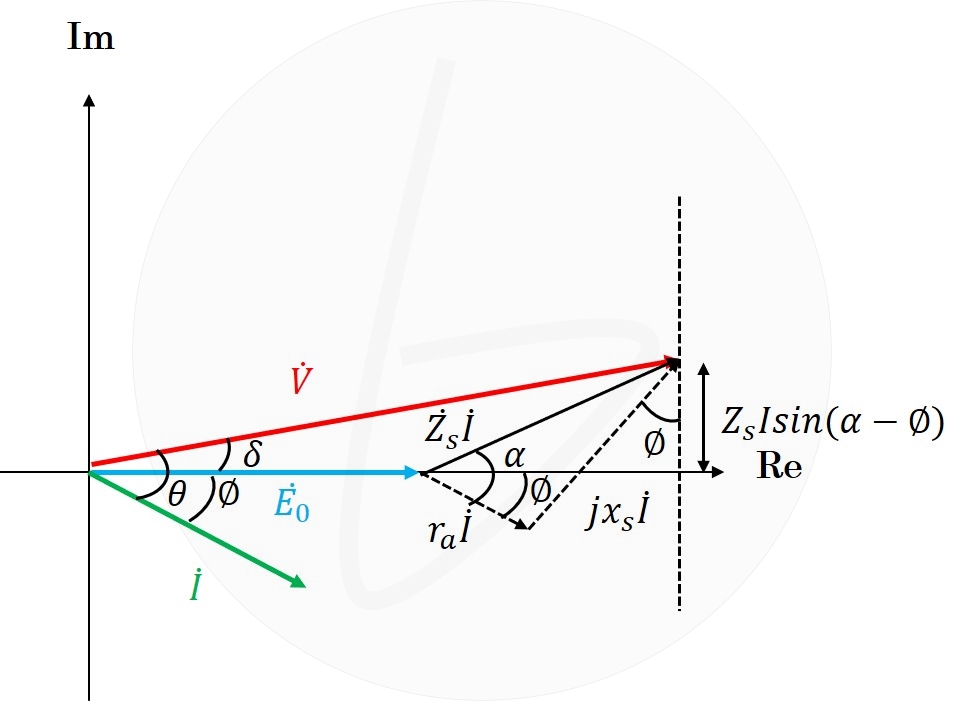
図4 同期電動機のベクトル図(虚軸成分の計算)
$$Z_sIsin(\alpha-\phi)=Vsin\phi \tag{7}$$
加法定理で展開して、
$$Z_sIsin\alpha cos\phi – Z_sIcos\alpha sin\phi=Vsin\phi \tag{8}$$
$sin\alpha$をかけて、
$$Z_sIsin^2\alpha cos\phi – Z_sIsin\alpha cos\alpha sin\phi=Vsin\alpha sin\phi \tag{9}$$
同期電動機の機械出力
式(6)で実軸に関して、
$$E_0cos\alpha+Z_sIcos^2\alpha cos\phi+Z_sIsin\alpha cos\alpha sin\phi =Vcos\alpha cos\delta \tag{再6}$$
式(9)で虚軸に関して、
$$Z_sIsin^2\alpha cos\phi – Z_sIsin\alpha cos\alpha sin\phi=Vsin\alpha sin\phi \tag{再9}$$
であるので、和を計算すると、
$$E_0cos\alpha+Z_sIcos^2\alpha cos\phi +Z_sIsin^2\alpha cos\phi=Vcos\alpha cos\delta+Vsin\alpha sin\phi \tag{10}$$
三角関数の基本公式である、
$$cos^2\alpha+sin^2\alpha=1 \tag{11}$$
$$cos\alpha cos\delta+sin\alpha sin\phi=cos(\alpha-\phi) \tag{12}$$
より、式(10)は、
$$E_0cos\alpha+Z_sIcos\phi =Vcos(\alpha-\phi) \tag{13}$$
となって、すなわち、
$$Icos\phi=\frac{V}{Z_s}cos(\alpha-\phi)-\frac{E_0}{Z_s}cos\alpha \tag{14}$$
となります。
同期電動機1相あたりの出力は、$P=E_0Icos\phi$で示されるのだから、
$$P=E_0Icos\phi=\frac{E_0V}{Z_s}cos(\alpha-\phi)-\frac{{E_0}^2}{Z_s}cos\alpha \tag{15}$$
これが、同期電動機の1相当たりの出力式となります。
なお、誘導電動機と同じで、端子電圧$V$は、相電圧であることに注意してください。
問題文で線間電圧が示されている場合には、$\frac{1}{\sqrt{3}}$倍を忘れないようにしてください。
また、あくまで1相当たりの機械的出力です。
同期電動機は通常の場合三相交流なので、3倍して、
$$P=3E_0Icos\phi=\frac{E_0V}{Z_s}cos(\alpha-\phi)-\frac{{E_0}^2}{Z_s}cos\alpha \tag{16}$$
となる点には注意してください。
同期発電機と同期電動機の出力式の関係性
同期電動機は基本的に同期発電機と同じベクトル図になり、似たような形式で示されます。
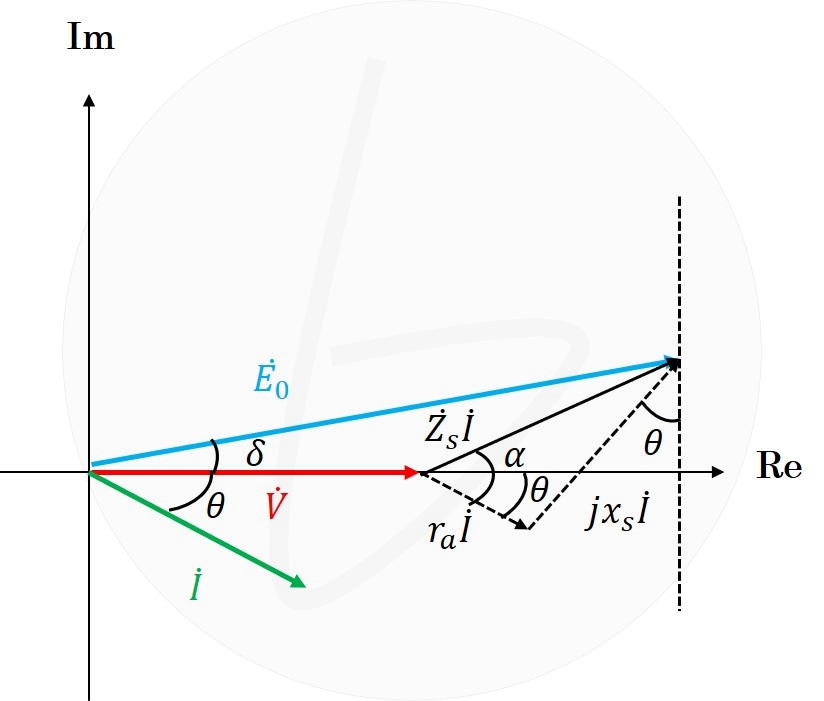
図5 同期発電機のベクトル図

図6 同期電動機のベクトル図
ベクトル図を見れば明らかなですが、
- 無負荷誘導起電力:$E_0$
- 端子電圧:$V$
が入れ替わっただけです。
そのため、
- 同期発電機の出力:$P=\frac{E_0V}{Z_s}cos(\alpha-\delta) -\frac{V^2}{Z_s}cos\alpha$
- 同期電動機の出力:$P=\frac{E_0V}{Z_s}cos(\alpha-\phi)-\frac{{E_0}^2}{Z_s}cos\alpha$
と、ちょうど$V$と$E_0$の位置が入れ替わっただけであることが理解できます。
参考に、無負荷誘導起電力$\dot{E_0}$と端子電圧$\dot{V}$の位相関係を見てみれば、
- 同期発電機は無負荷誘導起電力$\dot{E_0}$が進み位相
- 同期電動機は端子電圧$\dot{V}$が進み位相
となります。
このように、エネルギーを与える側が進み位相であり、エネルギーを受ける側が遅れ位相になる、イメージするなら、電源に対して負荷が遅れながら追従していく様子がわかります。
この辺りは、電気機器を理解するうえで非常に重要なポイントなので、感覚として養っておいてください。
巻線抵抗を無視する場合
巻線抵抗を無視し$r_a<<x_s$とする場合、$Z_s≒x_s$とできて、またインピーダンス角$\alpha=\frac{\pi}{2}$となるので、式(15)は、
$$P=\frac{E_0V}{x_s}sin\delta \tag{17}$$
となることがわかります。
ここで最高出力は$sin\delta=1$のときであり、すなわち負荷角$\delta=\frac{\pi}{2}$のときで、負荷角90°(=内部相差角90°)で最高出力となるのは、同期発電機と同じです。
まとめ
ここまで、同期電動機の出力式について導出を行ってきました。
同期電動機の出力式は、同期電動機/発電機の等価回路さえかければ簡単に求まります。
導出自体は結構ワンパターンな解法になるので、何度か計算していれば慣れます。
また、同期電動機の出力式は、同期発電機の出力式と関連付けて理解してください。
以上、同期電動機の出力式について、参考になれば幸いです。