 みなさん、こんにちは!
みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
当サイトでは、東大生のAcademic Styleをコンセプトに、学術的な話題を紹介していきます。
今回は、自由落下運動と鉛直投射について解説します。
自由落下運動とは
自由落下運動とは、物体に重力のみが働いて落下していく運動のことです。
物体に働く力は重力のみで、運動の方向も鉛直向きだけなので、1次元の式でよく、物理の運動方程式を利用した問題の中でも基礎的な問題となります。
自由落下運動の運動方程式
自由落下運動の運動方程式を考えていきます。
鉛直上向きをy軸の正の方向とします。
※鉛直下向きを正としても同じです。
運動方程式の基本として、物体に直接作用している力のみを考えるというものがあります。
自由落下運動については、物体に触れているものは何もありません。
遠隔的に働く力としては、重力と電磁力のみであり、今回は電磁力も働いていないので重力のみとなります。
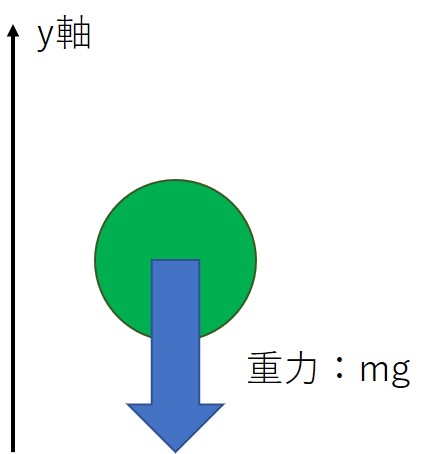
したがって、運動方程式は次のようになります。
$$m \frac{d^2 y}{dt^2}=-mg$$
したがって、この式を積分し、$\frac{dy}{dt}$を求めれば、速度の式になります。
$$v=\frac{dy}{dt}=-gt+V_0$$
ここで、自由落下を開始した$t=0$での初速度$V_0=0$とすると、初速度0で自由落下運動を始めた物体のt秒後の速度は次の式になります。
$v=-gt$
この式を積分すれば、t秒後の移動距離が求まります。
$t=0$での位置を$y=0$とすれば、自由落下運動の移動距離の式は、次のようになります。
$$y=-\frac{1}{2}gt^2$$
これで、初速度が0、初期位置が0の時の自由落下運動について解くことができました。
鉛直投射の運動方程式
鉛直投射は、物体に働く力は自由落下運動と同じです。
したがって、運動方程式自体は全く同じ式になります。
$$m\frac{d^2 y}{dt^2}=-mg$$
違うのは、初期状態($t=0$)において、鉛直上向きの初速度を持っていることです。
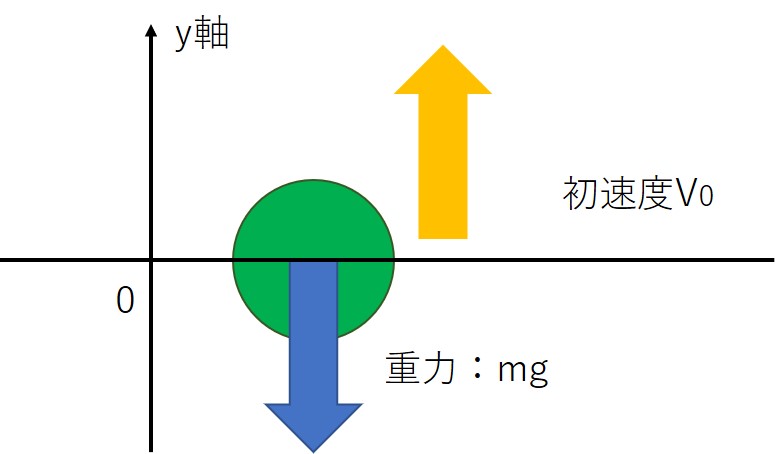
したがって、速度に関して解くと、自由落下運動の時と同じで次の式になります。
$$v=\frac{dy}{dt}=-gt+C_1$$
ここで、$C_1$は積分定数です。
初期条件として、$t=0$の時の速度(初速度)を$V_0$とすると、$C_1=V_0$と求まります。
したがって、鉛直投射の際の速度の式は、次の式になります。
$$v=\frac{dy}{dt}=-gt+V_0$$
この式より、移動距離に関して解くと、次の式になります。
$$y=-\frac{1}{2}gt^2+V_0t+C_2$$
$C_2$は積分定数であり、$t=0$での位置(初期位置)を$y=0$とすれば、$C_2=0$となります。
したがって、鉛直投射の際の移動距離の式は、次のようになります。
$$y=-\frac{1}{2}gt^2+V_0t$$
このように、自由落下運動と鉛直投射は、初期値の違いだけで全く同じ問題であることがわかるでしょう。
鉛直投射の物理的考察
鉛直投射における、速度変化を考察しましょう。
先ほどの式をもう一度見てみます。
$$v=-gt+V_0$$
$$y=-\frac{1}{2}gt^2+V_0 t$$
はじめに上向きに投げて、元の位置に戻ってくるときの時間を求めてみましょう。
この場合、$y=0$の時です。
したがって、次のように計算できます。
$$0=-\frac{1}{2}gt^2+V_0 t$$
$$0=t(\frac{1}{2}gt+V_0)$$
計算すると、$t=0$と$t=\frac{2V_0}{g}$と計算できます。
$t=0$は、初期値ですので無視します。
$t=\frac{2V_0}{g}$が、上に投げたものが投げた位置に再び戻ってくるときの時間です。
では、戻ってきたときの速度はどうなっているでしょうか?
$v$を求める式に、$t=\frac{2V_0}{g}$を代入します。
すると・・・
$$v=-g\frac{2V_0}{g}+V_0$$
つまり・・・
$$v=-V_0$$
となります。
これは、初速度$V_0$で上向きに投げた物体が、重力で失速し、下向きに落ちてきたときに、投げた位置では初速度と同じ大きさを持つ下向きの速度を持つことになります。
簡単に言えば、投げた速度の政府が入れ替わった状態です。
これを物理的に見れば、運動エネルギーが保存されていることになります。
運動エネルギー$U$は、次の式で表されます。
$$U=-\frac{1}{2}mv^2$$
$v$の正負が違っても、運動エネルギーは同じですよね。
ここに位置エネルギーも含めると、自由落下運動や、鉛直投射運動は、力学的エネルギーが保存しています。
速度と位置の変化の様子をグラフで表してみました。
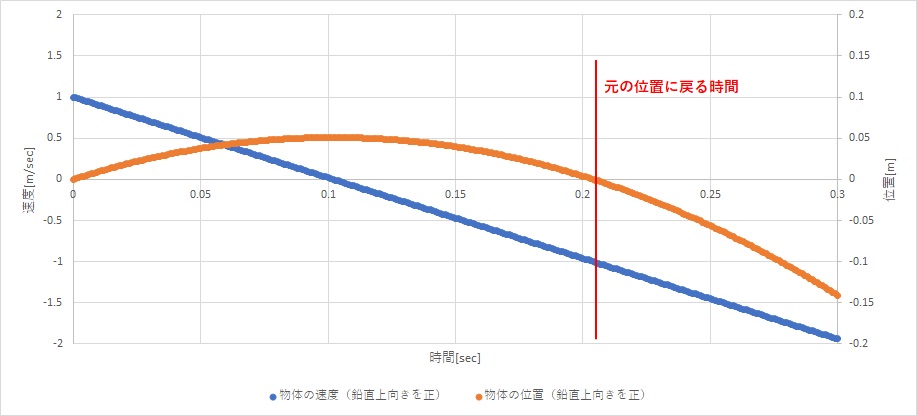
自由落下運動と鉛直投射のまとめ
ここまで、自由落下運動と鉛直投射について解説をしてきました。

自由落下運動も鉛直投射も、働いている力は重力だけです。
つまり、加速度は重力加速度$g$だけとなります。
自由落下運動と鉛直投射の違いは、初速度$V_0$を持っているかの違いだけです。
それ以外については、全く同じ開放で解くことができます。
一見、単純に見える自由落下運動と鉛直投射のン道と鉛直投射ですが、その中には物理における重要な法則、「運動エネルギーの保存則」が隠れています。
また、位置エネルギーまで見れば、力学的エネルギー保存則が見えます。
こうやって、少しずつ視野が広がっていくのも、物理の面白さですね。
以上、自由落下運動と鉛直投射について、参考になれば幸いです。


