
みなさん、こんにちは!
ブリュの公式ブログ.org(for Academic Style)にお越しいただきまして、ありがとうございます!
当サイトでは、東大生のAcademic Styleをコンセプトに、学術的な話題を紹介していきます。
今回は、物理学の基礎となる、力についてと、物理において必須となる数学のベクトルについて解説を行います。
力とは?
力は、日常生活における力の感覚と何も変わりません。
小難しい定義なんかもあるようですが、正直細かい定義を理解する意味はありません。
簡単に言えば、押す力や引っ張る力はすべて力です。
自転車を漕ぐとき、ペダルを踏みつけているのも力です。
ところで、今、鉛筆を持っていますか?
今、勉強中なら持っていますよね?

鉛筆を持つことをちょっと考えてみましょう。
鉛筆を指で挟んでいるのが力です。
挟まれた鉛筆は、指との摩擦力が働きます。
摩擦力も力の一種です。
そのまま腕に力を入れて鉛筆を持ち上げるのも力です。
物体は、力を受けると移動することは、簡単に想像できるでしょう。
力を加えてもモノが移動しない時
おいおい、ちょっと待てよ。
壁を押して力を加えても移動しないぞ?と思いませんか?
移動しない場合には、それは別の力が逆方向に力が働いて、総合的に打ち消されています。
例えば、消しゴムで机を擦ると、一定以上の力を加えないと、消しゴムは机の上を滑りません。

これは、消しゴムに加えた力を、消しゴムと机の摩擦力が打ち消しているからです。
鉛筆の話に戻しましょう。
鉛筆を真上に持ち上げて、手を静止させます。
この時、持っている鉛筆も当然動きません。
これは、鉛筆に働くすべての力が釣り合っているからです。
どうでしょう。
物理学における力が、日常的な感覚の力と全く同じであることがご理解いただけたと思います。
ベクトルとベクトルの合成
ベクトルとは
数学において、大きさ以外に向きを持ったものを、ベクトルと言います。
方向を持たず、大きさだけを持っているものをスカラーと言います。
スカラーに、方向を与えるとベクトルになります。
xyの2次元平面において、x軸方向とy軸方向に1の大きさを持っているベクトルを、単位ベクトルと言います。
下の図で見ると、ベクトル$\mathbf{u}$と$\mathbf{v}$は単位ベクトルとなります。
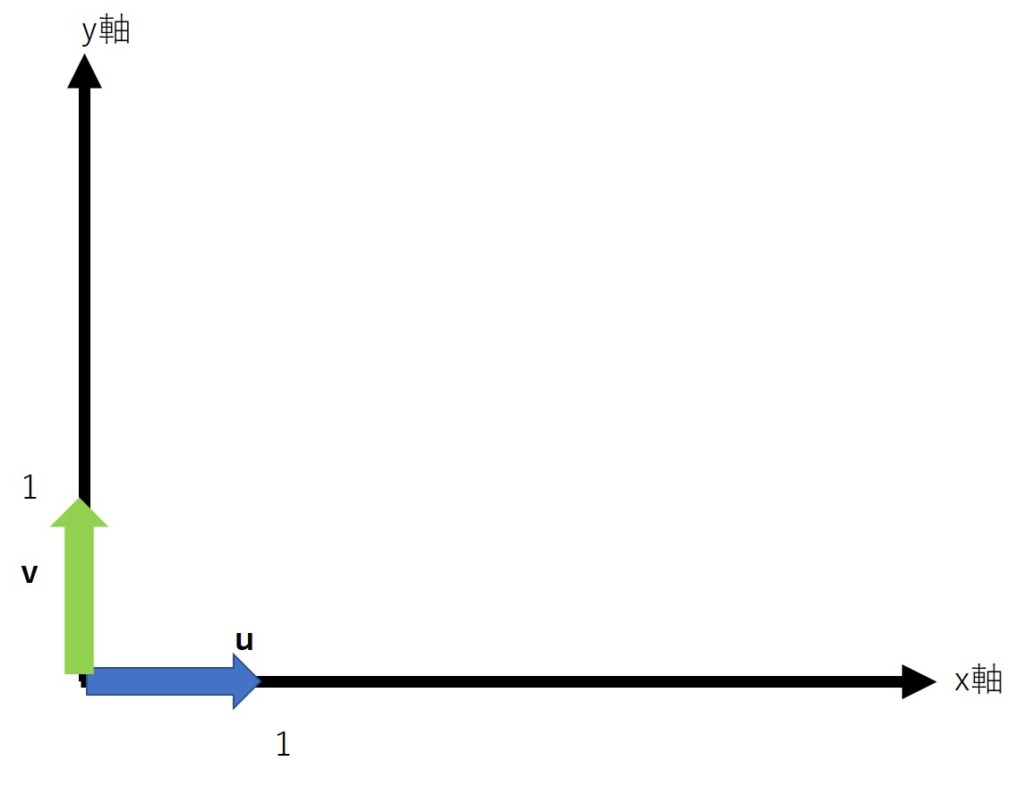
ベクトルの成分は、横ベクトルで表記すると(x,y)となります。
x軸方向に3という大きさを持っている値があったとします。
この時、横ベクトル表記で(3,0)と表すことができます。
また、スカラー量の3とx軸方向の単位ベクトル$\mathbf{u}=(1,0)$の積とも考えることができます。
ベクトルの合成(和と差)
ベクトルは合成が可能で、下の図のように平行四辺形を書いた時の対角線が合成ベクトルになります。
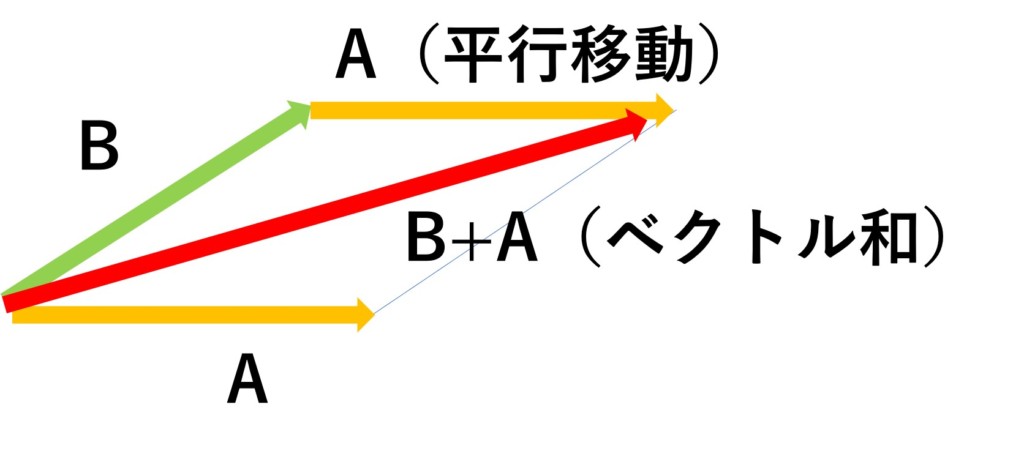
順を追ってみていきましょう。
ベクトル$\mathbf{A}$と$\mathbf{B}$があったとします。

ベクトル$\mathbf{B}$の先端に、ベクトル$\mathbf{A}$の始点を平行移動します。
※ベクトルは大きさと方向のみを持つので、始点を平行移動させても向きと大きさが同じならベクトルとしては同じものになります。
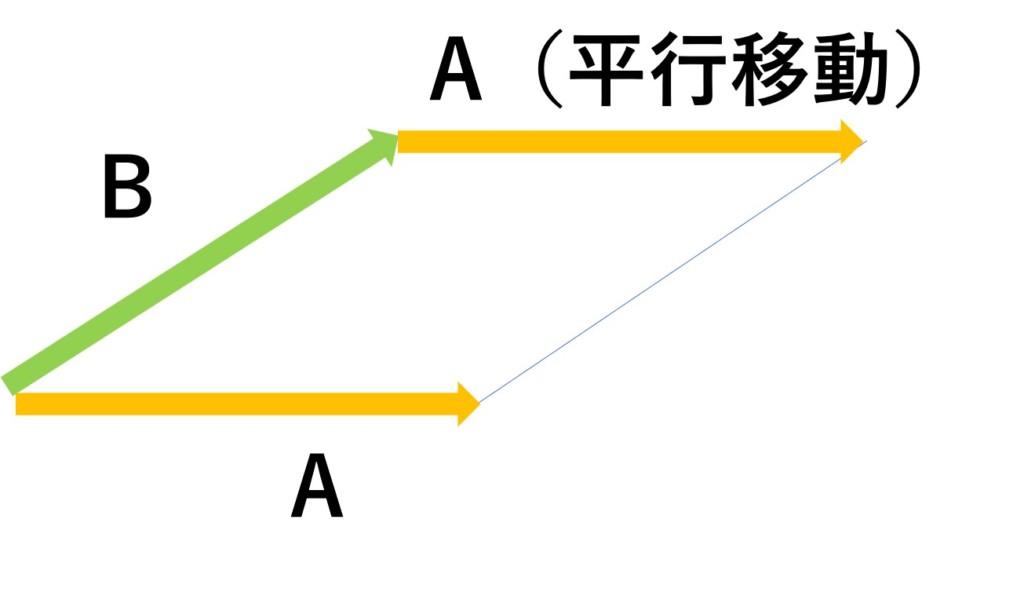
ベクトル$\mathbf{B}$の始点とベクトル$\mathbf{A}$の終点を結ぶと、ベクトルの合成ができます。
ここで、ベクトル$\mathbf{B}+\mathbf{A}$の向きは、ベクトル$\mathbf{B}$の始点からベクトル$\mathbf{A}$の終点の方向になります。
大きさは、平行四辺形の対角線の大きさになります。

スカラー値の足し算は、四則演算になりますが、ベクトルにおける足し算は、図のような図形的な足し算となります。
次に、ベクトルの差を考えてみましょう。
図のベクトル$\mathbf{B}$から、ベクトル$\mathbf{A}$を引きます。
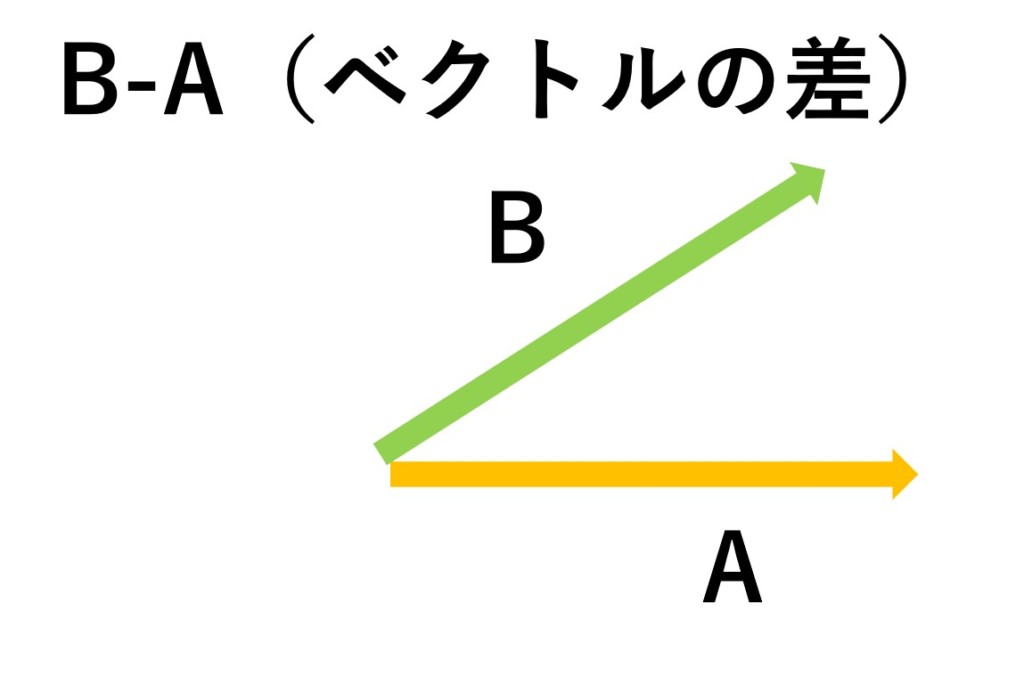
ベクトルの差$\mathbf{B}-\mathbf{A}$は、$\mathbf{B}+(-\mathbf{A})$と考えることができます。
したがって、ベクトル$\mathbf{A}$の向きを反転させた、ベクトル$-\mathbf{A}$を考えます。
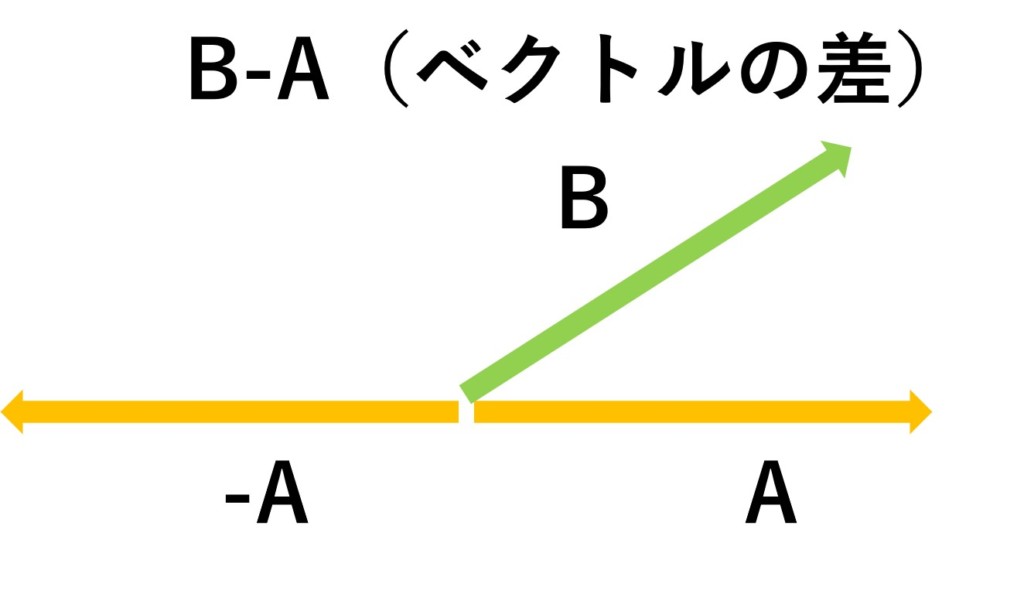
あとは先ほどの足し算と同じです。
$\mathbf{B}$の先端に、ベクトル$-\mathbf{A}$を平行移動します。
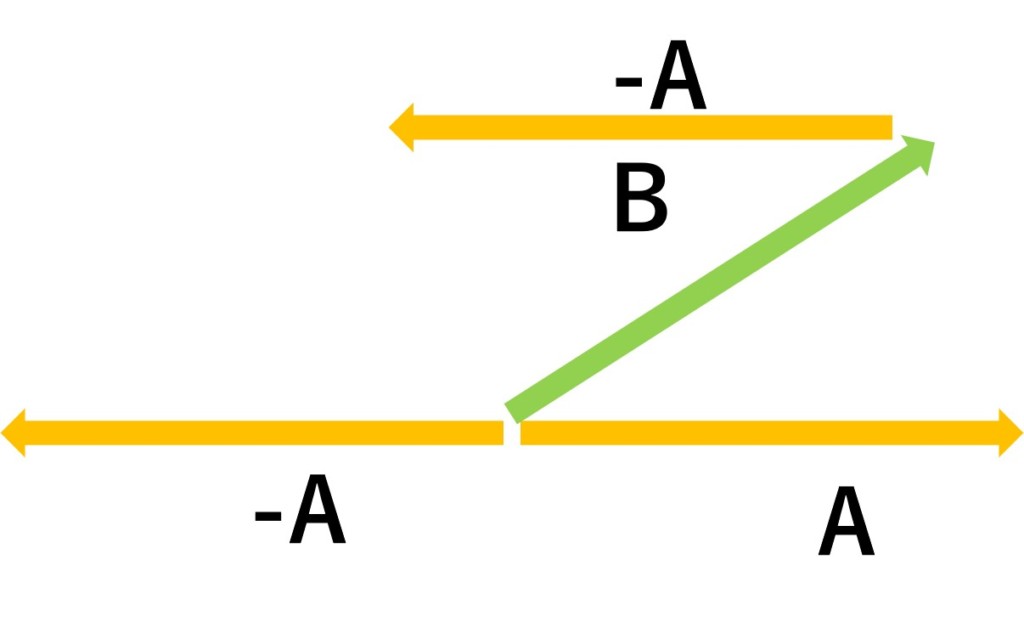
$\mathbf{B}$の始点と$-\mathbf{A}$の終点を結べば、$\mathbf{B}-\mathbf{A}$が計算できます。
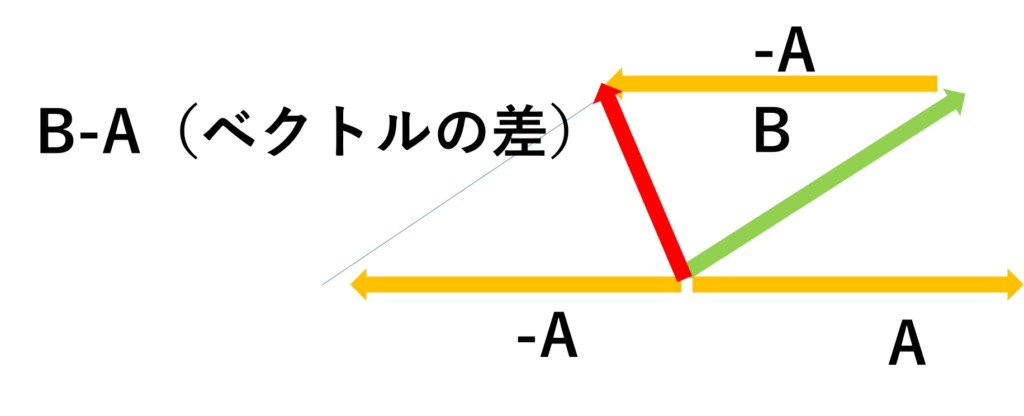
ベクトル$\mathbf{A}=(x_1 , y_1)$と$\mathbf{B}=(x_2 , y_2 )$を考えます。
$\mathbf{A}$と$\mathbf{B}$の足し算を行ったベクトルは、次の式で表すことができます。
$$\mathbf{B}+\mathbf{A}=(x_2+x_1,y_2+y_1)$$
同じ成分同士を足し合わせたものがベクトルの和です。
$\mathbf{A}$と$\mathbf{B}$の足し算を行ったときのベクトルの大きさは、次の式で計算できます。
$$|\mathbf{B}+\mathbf{A}|=\sqrt{(x_2+x_1)^2 + (y_2 + y_1)^2}$$
ベクトル$\mathbf{B}$と$\mathbf{A}$のベクトルの差は、次式で計算できます。
$$\mathbf{B}-\mathbf{A}=(x_2-x_1,y_2-y_1)$$
その大きさは、次の式で表すことが出kます。
$$|\mathbf{B}-\mathbf{A}|=\sqrt{(x_2 – x_1)^2 + (y_2-y_1)^2}$$
終点と始点の、成分の差の2上の和の平方根と覚えておきましょう。
力はベクトルで表す
力は、方向を持った値です。

鉛筆を持ち上げるとき、鉛筆を持ち上げる力の大きさと、持ち上げる方向を力として加えます。
つまり、「力の大きさ」ではなく、単に「力」と書かれている場合には、物理の世界では大きさと方向を持った値になります。
そこで、紙面上で力を表すときには、ベクトル量で力を表現します。
力の合成
世の中の物体には、様々な力が働いています。

一つの物体に、複数の力が働いた時、その物体に働く力は、ベクトルの合成で表現します。
下の図のように、原点にある質点に、$\mathbf{A}=(1,0)$と$\mathbf{B}=(0,1)$が働いたとします。
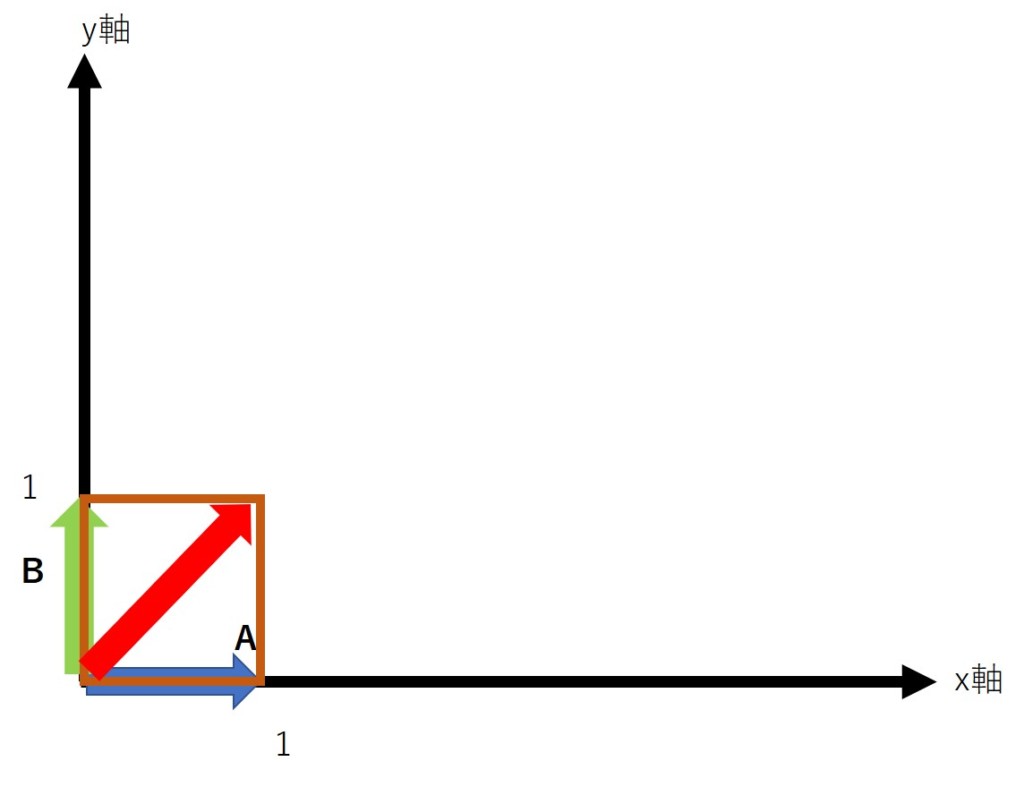
この時、質点に働く合力$\mathbf{F}$は、次の式で表すことができます。
$$\mathbf{F}=(1,0)+(0,1)=(1,1)$$
$\mathbf{F}$の大きさは、次のようになります。
$$\mathbf{F}=\sqrt{(1+0)^2+(0+1)^2}=\sqrt{2}$$
力とは?のまとめ
ここまで、力とベクトルについて解説してきました。

力はベクトル量で表すことができ、ベクトル量を用いて足し算、引き算を行います。
ベクトルの加減算では成分ごとに行います。
ベクトルの大きさは、直交座標系の場合、三平方の定理で求めることができます。
以上、物理学における力とベクトルについて、参考になれば幸いです。

