みなさん、こんにちは！
ブリュの公式ブログ.org（for Academic Style）にお越しいただきまして、ありがとうございます！
今回は、令和3年度 電験2種 2次試験 電力・管理 問3の回答・解説を行います。
目次
問題
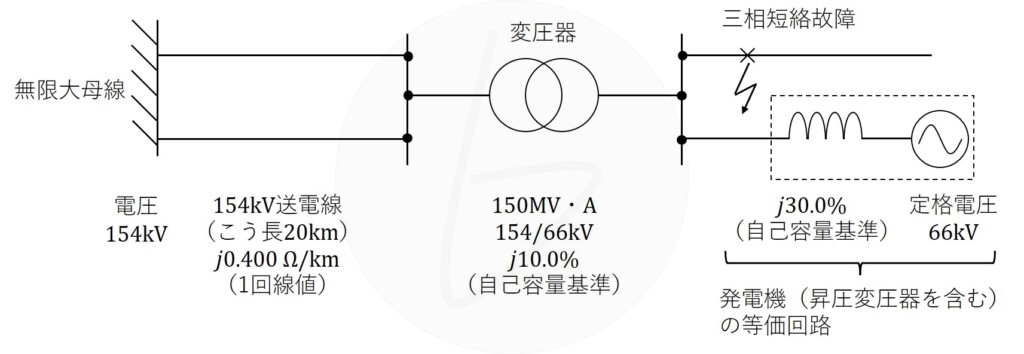
単位法を用いた三相回路の故障電流の検討について以下の問に答えよ。
（1）線間電圧154kV、三相容量100MV・Aを基準値とするとき、次を求めよ。
a)基準電流$I_B$[kA]
b)基準インピーダンス$Z_B$[Ω]
（2）図に示す無限大母線と送電線、変圧器、発電機から構成される電力系統を対象として、以下の量を、100MV・Aを基準容量とし各部の公称電圧ないしは定格電圧を基準電圧とする単位法による値に換算せよ。
a)公称電圧154kVのこう長20kmの1回線送電線のインピーダンスを上記の単位法の値[p.u.]に換算せよ。ただし、送電線（1回線）のインピーダンスは$j0.400$Ω/kmとする。
b)容量150MV・Aの変圧器（154/66kV）のインピーダンスを上記の単位法の値[p.u.]に換算せよ。ただし、同変圧器のインピーダンスは自己容量基準で$j10.0$%とする。
c)変圧器二次側（定格電圧66kV）の電流25kAを上記の単位法の値[p.u.]に換算せよ。
（3）図の電力系統で、変圧器二次側（定格電圧66kV）の母線至近端での三相短絡時における故障電流を25kA以下に抑えることができる発電機の最大容量S[MV・A]を求めよ。ここに、送電線と変圧器のインピーダンスは小問（2）に示すとおりであるが、154kV送電線は2回線とする。また、発電機（昇圧変圧器を含む）は、定格電圧が66kVの電圧源と自己容量基準でj30.0%のインピーダンスの直列回路で表すこととする。なお無限大母線の電圧は154kV、電圧源の電圧は66kVとする。
回答
本問は三相短絡故障に関する問題ですが、内容的には単位法に関する比較的基礎的な問題となっています。
単位法は、基準容量をそろえ、各部の公称電圧などを基準とした基準電圧から、基準電流、基準インピーダンスを求め、各基準値に対する割合を使って計算する手法です。
本問の序盤では、100MV・A、154kVを基準としていますが、短絡電流を求める故障点は66kVの地点になります。
基準電圧が異なるため、基準電流が異なります。
短絡電流を単位法で示す小問（2）c)においては、基準電流を再計算することに注意してください。
■■■（1）■■■
a)
基準電流$I_B$は、基準容量$S_{B}=100\rm{[MV・A]}$、基準電圧$V_{B}=154\rm{[kV]}$であるので、
$$\begin{align}
I_B &=\frac{S_{B}}{3×\frac{V_{B}}{\sqrt{3}}}\\
&= \frac{100×{10}^6}{3×\frac{154}{\sqrt3}×{10}^3}\\
&=374.891774891\rm{[A]} \\
&=0.374891774891\rm{[kA]}\tag{1}
\end{align}$$
となる。
（答）$I_B=0.375$[kA]
b)
基準インピーダンス$Z_B$は、
$$\begin{align}
Z_B&=\frac{\frac{V_{B}}{\sqrt{3}}}{I_{B}}\\
&=\frac{\frac{154}{\sqrt{3}}×10^3}{374.891774891}\\
&=237.173914203\rm{[Ω]}\tag{2}
\end{align}
$$
となる。
（答）$Z_B=237$[Ω]
■■■（2）■■■
a)
送電線1回線のインピーダンスは、
$$j0.400\rm{[Ω/km]}×20\rm{[km]}= j8 \rm{[Ω]}\tag{3}$$
である。
基準インピーダンス$Z_B$は小問（1）b)で求めたので、単位法に直すと、
$$\frac{j8}{237.173914203}=j0.03373052229\rm{[p.u.]}\tag{4}$$
となる。
（答）$j0.0337$[p.u.]
b)
自己容量150MV・A基準でj10.0[%]なので、基準容量を100[MV・A]に直すと、
$$\begin{align}
j10.0×\frac{100}{150}&=j6.66666666666[\%]\\
&=j0.06666666666\rm{[p.u.]}\tag{5}
\end{align}$$
となる。
（答）$j0.0667$[p.u.]
c)
本問では、基準電圧が154kV→66kVに変化するので、基準電流を再計算する必要があります。
基準容量100MV・A、基準電圧66kVにおける基準電流は、
$$\frac{100×10^6}{3×\frac{66}{\sqrt{3}}×10^3}=874.747474746\rm{[A]}\tag{6}$$
となる。
25[kA]を単位法に直すと、
$$\frac{25×10^3}{874.747474746}=28.5796766744\rm{[p.u.]}\tag{7}$$
となる。
（答）28.6[p.u.]
■■■（3）■■■
問題文が長くややこしそうですが、簡単に言えば、本問は、故障点の短絡比が小問（2）c)で求めた28.6以下であればOKです。
そして、発電機のインピーダンスが自己容量基準なので、100MV・A換算して、
$$j30.0 \frac{100}{S} \rm{[\%]}$$
とし、短絡比が28.6以下になるように$S$を求めます。
発電機のインピーダンスを100MV・A基準に直すと、
$$j30.0×\frac{100}{S}[\%]=j0.3×\frac{100}{S}\rm{[p.u.]}\tag{8}$$
となる。
短絡電流の経路は、解図3-1.1の通りになる。
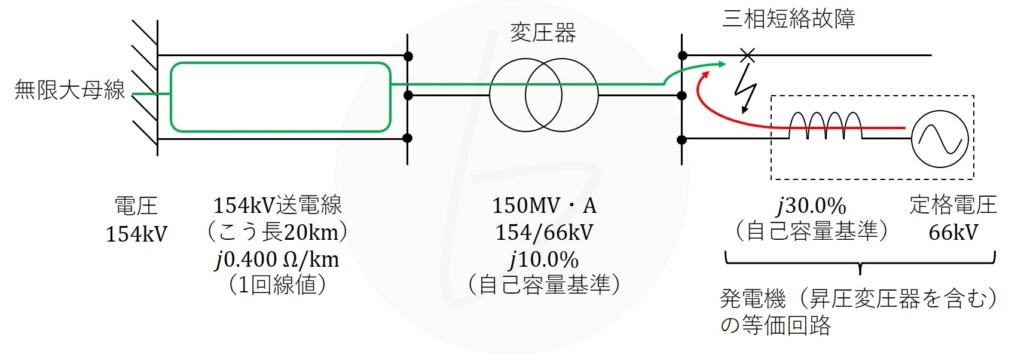
解図1
問題の回路図について、各インピーダンスを$100\rm{[MV・A]}$基準で書きなおすと、解図3-1.2のようになる。
なお、解図3-1.2においては、送電線は2回線分を考慮してある。
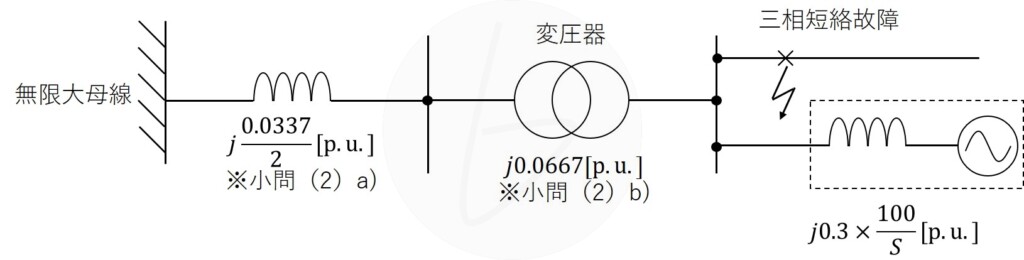
解図2
故障点から電源側を見たインピーダンスは、
$$\frac{1}{\frac{1}{j\frac{0.03373052229}{2} +j0.06666666666}+\frac{1}{j0.3×\frac{100}{S}}}\tag{9}$$
であり、この逆数が短絡比なので、短絡比は、
$$\begin{align}
&\frac{1}{j\frac{0.03373052229}{2}+j0.06666666666}+\frac{1}{j0.3\times\frac{100}{S}}\\
&=-j(11.9714703866+\frac{1}{30}S)\tag{10}
\end{align}$$
となる。
この大きさが、28.6以下であればいいから、
$$11.9714703866+\frac{1}{30}S≦28.5796766744\tag{11}$$
$$S≦498.246188634\rm{[MV・A]}\tag{12}$$
となる。
（答）$S=498\rm{[MV・A]}$